[矩阵分析] 二、酉空间和酉变换

晨晨丶

于 2024-03-27 13:33:50 发布

阅读量3.5k

点赞数 32

分类专栏：矩阵分析文章标签：矩阵算法线性代数矩阵分析高数

本文链接：https://blog.csdn.net/qq_43700729/article/details/137073879

版权

矩阵分析专栏收录该内容

2 篇文章

订阅专栏

本文详细探讨了酉空间和欧氏空间的基本概念，包括它们的性质、内积定义、正交性、标准正交基的重要性以及与正规矩阵的关联。文章还介绍了正交变换、子空间的同构和不变子空间的概念，并给出了实际应用中的例子和性质分析。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

酉空间和欧氏空间

酉空间（Unitary Space）

性质

欧氏空间（Euclidean Space）

酉空间和欧氏空间

酉空间（Unitary space）和欧氏空间（Euclidean space）是数学中两种重要的线性空间，它们在多个领域，如物理学、工程学和计算机科学中都有广泛应用。

酉空间（Unitary Space）

酉空间是定义在复数域上的内积空间。这意味着酉空间中的向量是复向量，而且这个空间定义了一个内积操作，这个内积操作满足一定的性质，如正定性、共轭对称性和线性性。在酉空间中，内积的定义通常是这样的：对于两个向量 x 和 y，其内积 〈x,y〉 是所有 $x_{i}\bar{y}_{i}$ （其中 $\bar{y}_{i}$ 是 $y_{i}$ 的复共轭）的和。（由于在复数中 $i^{2}=-1$ ，为了使内积为正，需要在转置中加入共轭操作 - 酉空间和欧氏空间的主要区别）

性质

长度和角度：酉空间通过内积定义了向量的长度（也称为范数）和向量之间的角度。这允许在酉空间中讨论向量的正交性。
正交性：如果两个向量的内积为零，则它们在酉空间中是正交的。
酉变换：保持内积不变的线性变换称为酉变换。这种变换保留了向量的长度和向量之间的角度，因此也保留了空间的几何结构。

欧氏空间（Euclidean Space）

欧氏空间是定义在实数域上的内积空间，是经典几何和向量分析的基础。在欧氏空间中，每个点都可以由一组实数坐标来表示，而两点间的距离是通过欧氏距离公式定义的。欧氏空间中的内积定义为两个向量的点乘，它反映了向量的长度和方向之间的关系。在欧氏空间中，内积定义为两个向量的点积，即

$\left \langle x,y \right \rangle=x_{1}y_{1}+x_{2}y_{2}+...+x_{n}y_{n}$

性质

长度和角度：通过内积，我们可以定义向量的长度（或范数）和两个向量之间的夹角。这使得我们能够讨论向量的正交性和距离。
正交性：如果两个向量的内积为零，它们是正交的。
旋转和反射：保持内积不变的线性变换在欧氏空间中称为旋转和反射。这些变换保持向量长度不变并且保持向量之间的角度。

酉空间与欧氏空间的比较

定义域不同：酉空间是在复数域上定义的，而欧氏空间是在实数域上定义的。
内积的定义：酉空间的内积包括复共轭，而欧氏空间的内积是向量的点积。
几何性质：尽管酉空间和欧氏空间都通过内积定义了长度、角度和正交性，但它们处理这些概念的方式不同，原因是它们分别基于复数域和实数域。

正规矩阵

正规矩阵是一种特殊类型的矩阵，它满足与其共轭转置相乘等于其共轭转置与其自身相乘的性质，即 $A^{T}A = AA^{T}$ 。这里 $A^{T}$ 表示 $A$ 的共轭转置。正规矩阵的一个重要性质是它们可以通过酉变换（在酉空间中）或正交变换（在欧氏空间中）对角化。这意味着，对于一个正规矩阵，存在一个酉矩阵或正交矩阵 U，使得 $U^{T}AU$ 是一个对角矩阵。（正矫正、酉矩阵、对角阵、实对称矩阵和 Hermite 矩阵都是正规矩阵）

联系

酉空间和欧氏空间与正规矩阵的主要联系在于，它们提供了正规矩阵性质的自然背景和应用场景。在这两种空间中定义的线性变换（表示为矩阵），当这些矩阵是正规的时，可以通过相应的变换（酉或正交）简化，从而揭示它们的结构和性质。这些概念在物理学、工程学、计算机科学等许多领域内是非常重要的，它们帮助人们理解和处理涉及线性变换的问题。

向量的正交与标准正交基

向量的正交

在数学中，两个向量被称为正交的，如果它们的内积为零。内积（也称点积）是衡量向量在某种意义上“相似性”的一种方式，如果两个向量的内积为零，则意味着它们在几何上是垂直的。对于实数向量空间，两个向量 a 和 b 的内积定义为 $a \cdot b=a_{1}b_{1}+a_{2}b_{2}+...+a_{n}b_{n}$ ，其中 $a_{i}$ 和 $b_{i}$ 是向量 a 和 b 的分量。如果 a⋅b=0，则 a 和 b 正交。

在复数向量空间（如酉空间）中，内积的定义稍有不同，考虑到复数的特性，向量的内积还包括了一个向量的复共轭。即便如此，正交的概念仍然基于内积为零这一准则。

标准正交基

一个向量空间的基是这个空间中的一组向量，这些向量线性无关，并且任何在该空间中的向量都可以通过这组基向量的线性组合唯一表示。当这组基向量不仅相互正交，且每个向量的长度都为1（即单位向量）时，这组基向量被称为标准正交基。

具体来说，一组向量 $\left \{ u_{1},u_{2},...,u_{n} \right \}$ 构成一个标准正交基，如果满足以下两个条件：

正交性：对于任意的 $i\neq j$ ， $u_{i}\cdot u{j}=0$ 。
标准化：每个向量的长度为1，即对于所有的 $i$ ， $\left | \left | u_{i} \right | \right |=1$ ，其中 $\left | \left | u_{i} \right | \right |$ 是向量 $u_{i}$ 的欧几里得范数。

为什么标准正交基重要？

标准正交基有许多数学和计算上的优点。首先，它简化了许多线性代数运算，比如向量的投影、计算向量间的距离等。此外，使用标准正交基可以使得一些问题的解析解更加直观易懂。在很多实际应用中，比如信号处理、量子计算和数值分析等领域，找到合适的标准正交基是解决问题的关键。

如何获得标准正交基

从一组给定的基出发，可以通过格拉姆-施密特正交化过程得到一个标准正交基。这个过程通过线性组合和规范化步骤，逐步将任意一组基转化为一组标准正交基，同时保持向量空间的结构不变。

酉（正交）变换

正交变换是实数向量空间中的一种特殊线性变换，它同样保持向量长度不变，进而保持向量间的角度不变。形式上，一个线性变换 Q 是正交的，如果满足 $Q^{T}Q=QQ^{T}=I$ ，其中 $Q^{T}$ 是 $Q$ 的转置。这意味着 $Q$ 的列向量（或行向量）组成了向量空间的一个标准正交基。在实数域中，正交变换包括旋转、反射等。

酉正交变换

“酉正交变换”一词可能会引起一些混淆，因为“酉”一词通常用于描述复数向量空间中的概念，而“正交”一词则经常与实数向量空间的变换联系在一起。在严格意义上，酉变换是复数向量空间的概念，它与正交变换在实数向量空间中的作用相似，但适用的数学领域不同。

因此，当我们讨论“酉正交变换”时，通常指的是酉变换，即在复数向量空间中保持向量内积不变的线性变换。这种变换保留了向量的长度和向量之间的夹角，使其在许多数学和物理问题中变得非常有用，如在量子力学中，酉变换用来描述系统的演化，保持概率守恒；在信号处理中，酉变换用于保持信号的能量不变。

几种特殊的子空间

为了理解几种特殊的子空间，我们首先需要了解几个基本的定义：

向量空间：想象一个无限大的空间，其中的每一点都可以用数字（称为向量）来表示。这些向量可以相加或乘以数字（称为标量），而且这些操作遵循一定的数学规则。
子空间：向量空间内的一个小“世界”，它自成一体，拥有向量空间的所有性质。简单来说，如果你从这个小世界里拿出两个向量加在一起，或者把其中一个向量乘以一个数字，你得到的结果仍然在这个小世界里。

子空间的同构

在数学中，特别是在线性代数和抽象代数中，同构是一种表明两个（代数）结构在结构上是“相同”的概念。对于子空间来说，同构意味着两个线性空间（或子空间）在保持线性结构（如向量加法和标量乘法）不变的映射下是相互对应的。简而言之，如果存在一个线性变换，可以无歧义地（即一一对应且可逆地）将一个子空间的元素映射到另一个子空间的元素，同时保持线性运算不变，那么这两个子空间就是同构的。

同构的定义

具体来说，假设我们有两个向量空间 V 和 W，它们都是在同一个数域 F 上。一个线性映射 T: V→W 是同构的，如果它是双射的（即一一对应且可逆的），并且对于所有的 $v_{1},v_{2}\in V$ 和所有的标量 α∈F，都满足以下两个条件：

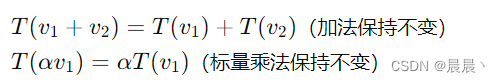
如果存在这样的映射 T，我们就说 V 和 W 是同构的，记作 V≅W。

同构的性质

维数不变性：如果两个向量空间同构，它们的维数必须相同。这意味着，对于有限维向量空间，同构提供了一个强大的工具来判断两个空间是否“相等”。
结构保持：同构不仅仅保持了向量空间的大小（通过维数）不变，还保持了向量空间的所有线性结构不变，包括子空间的关系、线性独立性、基的概念等。
可逆性：由于同构映射是双射的，因此总存在一个逆映射 $T^{-1}:W\rightarrow V$ ，它也是一个同构映射。

子空间的同构

对于子空间，同构的概念也适用。如果子空间 U⊆V 和 W 是同构的，这意味着 U 内的结构和关系可以完全通过 W 来描述，反之亦然。同构映射提供了一种桥梁，允许我们在不同的空间或子空间中转移问题，从而利用特定空间的性质来解决问题。

不变子空间

在线性代数中，不变子空间是对于给定的线性映射或矩阵具有特定稳定性质的子空间。具体来说，假设我们有一个线性映射 T: V→V（可以理解为 T 是 V 上的线性映射），其中 V 是一个向量空间。一个子空间 W 被称为 T 的不变子空间，如果对于 W 中的所有向量 w，T(w) 仍然在 W 中。换句话说，T 在 W 上的作用仅产生 W 内的向量，不会将 W 内的向量映射到 W 外部。

通俗理解

在一个向量空间中，考虑一个线性变换，这就像一个机器，你投入一个向量，它就给你输出另一个向量。如果存在一个子空间，使得当你将这个子空间中的任何向量投入这个“机器”时，输出的向量仍然在这个子空间中，那么这个子空间就被称为不变子空间。

重要性和应用

不变子空间在理解和分解线性变换和矩阵的行为方面非常重要。通过研究一个矩阵或线性映射的不变子空间，可以更深入地了解其结构和特征，比如可以帮助在解决特征值和特征向量问题时简化问题。此外，不变子空间的概念在应用数学、量子力学和控制理论等领域中也非常重要。

例子

特征空间：给定一个矩阵 A 和它的一个特征值 λ，对应的特征空间（即所有满足 Ax = λx 的向量 x 的集合）是 A 的不变子空间。这是因为，如果 x 是一个特征向量，则 A 作用在 x 上的结果仍然在由 x 生成的空间内，只是被拉伸了一个因子 λ。
零空间和列空间：对于任何矩阵 A，其零空间（null space）和列空间（column space）都是 A 的不变子空间。零空间包含所有被 A 映射到零向量的向量，而列空间包含所有可能作为 A 的线性变换结果的向量。

性质

如果 W1 和 W2 是 T 的不变子空间，则 W1∩W2 也是 T 的不变子空间。
然而，W1+W2（W1 和 W2 的和空间）不一定是 T 的不变子空间，除非额外条件满足，例如 T 在 W1 上和 W2 上分别闭合。
向量空间 V 和其零子空间 {0} 对于任何线性映射 T 总是 T 的不变子空间。

正交子空间

将向量之间的正交概率推广到子空间之间。

向量的正交性

首先，当我们说两个向量正交，我们的意思是它们的点积（或内积）等于零。在几何上，这意味着这两个向量在空间中是垂直的。例如，在二维或三维空间中，两条相互垂直的直线对应的方向向量就是正交的。

子空间

在线性代数中，子空间是指一个向量空间中的一个集合，它自身也构成一个向量空间。简单来说，如果你有一个向量空间，那么它的任何子集如果满足向量加法和标量乘法的封闭性，这个子集就可以被认为是一个子空间。

正交子空间的定义

在一个给定的向量空间中，一个子空间的正交补（或简称为正交子空间）是指所有与原子空间中每个向量都正交的向量组成的集合。这个概念是基于正交性的定义：如果你有一个子空间 S，那么 S的正交补记为 $S^{\perp }$ （读作"S-perp"），包含了所有与 S 中任意向量都正交的向量。

性质和例子

性质：如果你在向量空间 V 中有一个子空间 S 和它的正交补 $S^{\perp }$ ，那么 V 可以被看作是 S 和 $S^{\perp }$ 的直和（直和表示线性空间中两个或多个子空间的一种特殊关系，即这些子空间的直接组合形成一个新的向量空间）。换句话说，V 中的每个向量都可以唯一地表示为 S 中的一个向量和 $S^{\perp }$ 中的一个向量的和。
例子：想象一下三维空间中的一条直线（我们可以把它视为一个一维子空间）。这条直线的正交补是一个平面，平面上的每个向量都与直线上的任何向量正交。这个平面覆盖了直线以外的整个三维空间的剩余部分。