（详细全面）softmax和log_softmax的联系和区别,NLLLOSS和CrossEntropyLoss的联系和区别

1.softmax

作用：实现了将n维向量变成n维全为正数，且和为1的向量，在深度学习中可以解释为这个输入属于n个类别的概率。
例子：

import torch.nn.functional as F
inp1=torch.Tensor([1,3,6])
print(inp1)
print(F.softmax(inp1,dim=0))

print("#############")
inp2=torch.Tensor([2,2,2])
print(inp2)
print(F.softmax(inp2,dim=0))

可以看到，如果n维向量每一个分量是一样的，那么概率1平分给3个类别，表示属于三个类别的概率是相等的。

以inp1为例我们可以验证一下(即用numpy实现softmax()):

import numpy as np

inp1=np.array(inp1)#inp1=[1,3,6]
inp1_pow=np.power(np.e,inp1)

inp1_pow/np.sum(inp1_pow)#对应上述开头的那个公式

发现这个结果和上述调用softmax()结果是一样的。

2.log_softmax

我们发现只是再求一个Log而已。

import torch.nn.functional as F
inp1=torch.Tensor([1,3,6])
print(inp1)
print(F.log_softmax(inp1,dim=0))

同样，我们可以验证一下(即用numpy实现log_softmax()):

import numpy as np

inp1=np.array(inp1)
inp1_pow=np.power(np.e,inp1)

inp1_softmax=inp1_pow/np.sum(inp1_pow)#对应上述公式
print("softmax后：")
print(inp1_softmax)
inp1_log_softmax=np.log(inp1_softmax)#再取一次log而已
print("在上述基础上再取log后：")
print(inp1_log_softmax)

发现和前面log_softmax()还是一样的。

3.softmax和log_softmax

softmax的作用不言而喻，每一项代表概率，我们发现去了Log之后并不是概率了，有什么用呢？

官网解释：https://pytorch.org/docs/stable/generated/torch.nn.functional.log_softmax.html?highlight=log_sof#torch.nn.functional.log_softmax

Applies a softmax followed by a logarithm.

While（尽管） mathematically equivalent to log(softmax(x)), doing these two
operations separately is slower, and numerically unstable. This
function uses an alternative formulation to compute the output and
gradient correctly.

大概意思就是说，虽然可以用log(softmax(x))来代替log_softmax()，但是前者太慢了。需要进行n次指数,n次除法，n次log（忽略加减法）。后者只需要n次指数,1次log。

而做softmax需要n次指数，n次除法。这样看来，似乎Log_softmax()似乎最好。

注意到：
$\log \frac{e^x}{e^x+e^y}=x-log(e^x+e^y)$
所以两次指数，一次对数，这个算好了可以保存起来，下一次还是继续用。

不过，实际操作中还会有一个使得数值计算更加稳定的算法，因为我们要考虑这种情况，如果(x,y)=(1000,1001)。那么$e^{1000}$将会发生上溢。与之对应有$e^{-1000}$会发生下溢。
从而我们有了如下更加稳定的办法：即取$M=\max (x,y)$。有：

$\log \frac{e^x}{e^x+e^y}=\log \frac{e^x/e^M}{e^x/e^M+e^y/e^M}=x-M-log(e^{x-M}+e^{y-M})$

当然了，有人杠，

1. (x,y)=(0,1000)，这个方法没用，对，但是这个方法有的时候有用啊。
2. 也有人说(x,y)=(-10,10)，反而会计算$e^{-20}$，岂不是比原来的$e^{-10}$更加下溢，这个分析也对，但是要记住，上溢是最难受的，下溢还好，我们要更加避免上溢。

所以，这也是一个权衡之术。

4.NLLLOSS和CrossEntropyLoss

NLLLOSS：The negative（负的） log likelihood loss.
CrossEntropyLoss：

其中p为真实分布，q为预测分布。

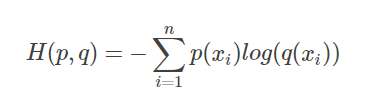
联系：

It is useful to train a classification problem with C classes.

即共同点是对于分类问题是非常好的两种损失函数。

过渡：

但是严格来说，NLLLOSS并不是一个损失函数，后者才是，前者是基于后者的，但是节省了计算量（区别提前剧透了）。

区别：

Obtaining log-probabilities in a neural network is easily achieved by
adding a LogSoftmax layer in the last layer of your network. You may
use CrossEntropyLoss instead, if you prefer not to add an extra layer.

即：我们以前在做分类任务的时候，例如手写数字识别，最后一层有两种习惯：

1. 使用softmax层，转化为各个类别概率，这种情况，你应该紧接着使用CrossEntropyLoss损失函数。
2. 使用log_softmax层，那么使用NLLLOSS最好而且最直接。

解释：

在情况1中，根据CrossEntropyLoss公式，加上这是分类问题，所以标签中只有一个类别（设为z)分量为1，其他类别全为0，我们代入公式，即求和之后只剩下一项。
$-\log q_z$
其中$q_z$表示我们的模型对该输入，属于类别z的概率的预测。

所以情况1计算CrossEntropyLoss的步骤就是取log,再取反。

在情况2中，我们模型的输出直接就是$\log q_z$（log_softmax层后），所以计算NLLLOSS的步骤只需要取反，十分快速。这就是为什么叫做The negative log likelihood loss.

官网地址：https://pytorch.org/docs/stable/generated/torch.nn.NLLLoss.html#torch.nn.NLLLoss。

---

补充：CrossEntropyLoss大家肯定都已经用过，NLLLOSS使用语法是一样的，伪代码大致是这样。

import torch.nn as nn
import torch.nn.functional as F
class CNN(nn.Module):
    def __init__(self):
        super(CNN,self).__init__()
		*
		*
		*
    def forward(self,x):
        #x:1*28*28
        x=F.relu(self.conv1(x))
		*
		*
		*
        x=self.fc2(x)
        #shape=(1,10)
        return F.log_softmax(x,dim=1)
       
pred=model(x)
loss=F.nll_loss(pred,target)