背包问题十一讲（你的背包，背到现在还没会））

磊哥哥讲算法

已于 2022-10-29 19:52:29 修改

阅读量321

点赞数 1

分类专栏：算法进阶算法文章标签：算法动态规划 dfs

于 2022-07-11 00:56:56 首次发布

本文链接：https://blog.csdn.net/qq_43621422/article/details/125712805

版权

算法同时被 2 个专栏收录

12 篇文章 4 订阅

订阅专栏

进阶算法

8 篇文章 0 订阅

订阅专栏

前言

太阳当空照，花儿对我笑，
小鸟说早早早，你为什么背上炸药包

最简背包问题

背包问题是最基础的DP问题，同时也是DP的入门思路培养和拆分问题的手段，总体的拆分方法是使用了闫式DP法。本篇文章将01背包问题作为入题手段，随后进行各种骚套路变换，一共有11种变形，也就是，你的背包让我走得好慢，背到现在还没会。一个题外话，一个人送的书包我用了四年了还在用。
讲述的方法还是模板题，然后思路加变形和优化，且是层层相扣的，如果上一个没懂的，建议手动DP一次或者用visF11走一遍，不然理解上会出现一些小问题。

01背包问题

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最大价值

也就是n–循环存数据然后进行DP的存放，取到最大值，并且要求是每种物品只能用一次，体积不能超。在DP 的时候有可能我不一定塞满，但是我就是整到了最大价值了，这些都是伏笔，等会要考的哦。

首先要理解的是在dp过程中 i -1 与 i 不变的原因

01背包
  dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i]] + v[i]);
完全背包
  dp[i][j] = max(dp[i - 1][j], dp[i][j - w[i]] + v[i]);

此时，取第i个药时还能再取第i个药，因此没有退回i-1
01背包中，不能再次取第i个，所以一定要退回i-1
在未能选取的情况下，将整个dp过程想象成一个二维表，那么在保证j 不变的情况下，就要回退到之前的最大值，也就是 i-1 进行赋值，如果选择了也就是在i-1的最大值情况下加入新的w并且修改j ‘的值。
完全背包的点在于可以多次选择避免了选择到再回退，因为自己当下有可能就是最大值，而01背包只能选择一次，所以需要回退。

朴素解法

状态定义F[i][j]，前i个物品，背包容量为j的最优解，遵循DP的逻辑，状态时前后依赖的，从初始化状态也就是f[i][j]，i为0，j为0的时候开始的，有n个物品则需要n次决策，每一次对第i件物品的决策，会通过max进行状态更新。
当背包满了之后的j<v[i]，放不进的时候最优解就是i-1的物品
当前背包容量够，可以选，因此需要决策选与不选第 i个物品：
选：f[i][j] = f[i - 1][j - v[i]] + w[i]。
不选：f[i][j] = f[i - 1][j] 。

基本数据定义，之后都内定会有，在下面的变形里就不重复了

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
int v[MAXN];    // 体积
int w[MAXN];    // 价值 
int f[MAXN][MAXN];  // f[i][j], j体积下前i个物品的最大价值

01背包DP

for(int i = 1; i <= n; i++) 
        for(int j = 1; j <= m; j++) {
            //  当前背包容量装不进第i个物品，则价值等于前i-1个物品
            if(j < v[i]) 
                f[i][j] = f[i - 1][j];
            // 能装，需进行决策是否选择第i个物品
            else    
                f[i][j] = max(f[i - 1][j], f[i - 1][j - v[i]] + w[i]);
        }           

    cout << f[n][m] << endl;

一维优化

类似于反向推的等价变换，定义的状态f[i][j]可以求得任意合法的i与j最优解，但题目只需要求得最终状态f[n][m]，因此我们只需要一维的空间来更新状态。

状态f[j]定义：N件物品，背包容量j下的最优解。
注意枚举背包容量j必须从m开始。
为什么一维情况下枚举背包容量需要逆序？在二维情况下，状态f[i][j]是由上一轮i - 1的状态得来的，f[i][j]与f[i - 1][j]是独立的。而优化到一维后，如果我们还是正序，则有f[较小体积]更新到f[较大体积]，则有可能本应该用第i-1轮的状态却用的是第i轮的状态。
简单来说，一维情况正序更新状态f[j]需要用到前面计算的状态已经被「影响」，逆序则不会有这样的问题。

for(int i = 1; i <= n; i++)
{
    for(int j = m; j >= v[i]; j--)  
        f[j] = max(f[j], f[j - v[i]] + w[i]);
}

完全背包问题

题目中变换的是可以使用无限次，只要最大价值就行
先明确递推关系

f[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w ,  f[i-1,j-2*v]+2*w , f[i-1,j-3*v]+3*w , .....)
f[i , j-v]= max(            f[i-1,j-v]   ,  f[i-1,j-2*v] + w , f[i-1,j-3*v]+2*w , .....)
由上两式，可得出如下递推关系： 
                        f[i][j]=max(f[i,j-v]+w , f[i-1][j]) 
       这个递推关在之后的queue队列优化有很大的用处

k朴素

说是无限，但是自己的背包的存放是有限的，那就计算出k，我能存放的最多有几个。

for(int i = 1 ; i<=n ;i++)
    for(int j = 0 ; j<=m ;j++){
        for(int k = 0 ; k*v[i]<=j ; k++)
            f[i][j] = max(f[i][j],f[i-1][j-k*v[i]]+k*w[i]);
    }
    cout<<f[n][m]<<endl;

但结合上面的递推公式，我们会发现，其实在每次递推的过程中，k的隐藏作用已经在逻辑中被使用了。
可以将核心代码优化，类似于一个更大01背包问题，当我们把背包的现容量看成一个浮动的变量，能加就加进去的话，理解DP就要从小往大去看。

for(int i = 1 ; i <=n ;i++)
for(int j = 0 ; j <=m ;j++){
    f[i][j] = f[i-1][j];
    if(j-v[i]>=0)
        f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
}

可以翻上去对比一下01背包

逆序思维理解一维化

再然后进行反向一维化操作

int main(){
    int n,m;
    cin>>n>>m;
    for(int i = 1 ; i <= n ;i ++) {
        cin>>v[i]>>w[i];
    }
    for(int i = 1 ; i<=n ;i++)
    for(int j = v[i] ; j<=m ;j++){
            f[j] = max(f[j],f[j-v[i]]+w[i]);
    }
    cout<<f[m]<<endl;
}

背包问题的实际思路流程

首先dp数组初始化全为0：给定物品种类有4种，包最大体积为5，数据来源于题目的输入
v[1] = 1, w[1] = 2
v[2] = 2, w[2] = 4
v[3] = 3, w[3] = 4
v[4] = 4, w[4] = 5

i = 1 时： j从v[1]到5
dp[1] = max(dp[1],dp[0]+w[1]) = w[1] = 2 (用了一件物品1）
dp[2] = max(dp[2],dp[1]+w[1]) = w[1] + w[1] = 4（用了两件物品1）
dp[3] = max(dp[3],dp[2]+w[1]) = w[1] + w[1] + w[1] = 6（用了三件物品1）
dp[4] = max(dp[4],dp[3]+w[1]) = w[1] + w[1] + w[1] + w[1] = 8（用了四件物品1）
dp[5] = max(dp[3],dp[2]+w[1]) = w[1] + w[1] + w[1] + w[1] + w[1] = 10（用了五件物品）

i = 2 时：j从v[2]到5
dp[2] = max(dp[2],dp[0]+w[2]) = w[1] + w[1] = w[2] =  4（用了两件物品1或者一件物品2）
dp[3] = max(dp[3],dp[1]+w[2]) = 3 * w[1] = w[1] + w[2] =  6（用了三件物品1，或者一件物品1和一件物品2）
dp[4] = max(dp[4],dp[2]+w[2]) = 4 * w[1] = dp[2] + w[2] =  8（用了四件物品1或者，两件物品1和一件物品2或两件物品2）
dp[5] = max(dp[5],dp[3]+w[2]) = 5 * w[1] = dp[3] + w[2] =  10（用了五件物品1或者，三件物品1和一件物品2或一件物品1和两件物品2）

i = 3时：j从v[3]到5
dp[3] = max(dp[3],dp[0]+w[3]) = dp[3] = 6 # 保持第二轮的状态 
dp[4] = max(dp[4],dp[1]+w[3]) = dp[4] = 8 # 保持第二轮的状态 
dp[5] = max(dp[5],dp[2]+w[3]) = dp[4] = 10 # 保持第二轮的状态

i = 4时：j从v[4]到5
dp[4] = max(dp[4],dp[0]+w[4]) = dp[4] = 10 # 保持第三轮的状态
dp[5] = max(dp[5],dp[1]+w[4]) = dp[5] = 10 # 保持第三轮的状态

上面模拟了完全背包的全部过程，也可以看出，最后一轮的dp[m]即为最终的返回结果。

完全背包的思路

[i , j ] = max( f[i-1,j] , f[i-1,j-v]+w , f[i-1,j-2v]+2w , f[i-1,j-3v]+3w, …)
f[i , j-v]= max( f[i-1,j-v] , f[i-1,j-2v] + w, f[i-1,j-2v]+2w , …)
通过上述比较，可以得到 f[ i ][ j ] = max(f[ i - 1 ][ j ],f[ i ][ j - v ] + w)。
多重背包思路
f[i , j ] = max( f[i-1,j] ,f[i-1,j-v]+w ,f[i-1,j-2v]+2w ,… f[i-1,j-Sv]+Sw, )
f[i , j-v]= max( f[i-1,j-v] ,f[i-1,j-2v]+w, … f[i-1,j-Sv]+(S-1)w, f[i-1,j-(S+1)v]+Sw )

多重背包

这次的变形是某个物品里有设定的几个，同样有体积约束和价值目标，也就不再是固定一个或者无限个了。

k朴素

状态标记
集合划分依据：根据第i个物品有多少个来划分.含0个、含1个···含k个.
状态表示与完全背包朴素代码一样均为：
f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);

int main(){
    cin >> n >> m;
    for(int i = 1; i <= n; i ++) cin >> v[i] >> w[i] >> s[i];
    for(int i = 1; i <= n; i ++){//枚举背包
        for(int j = 1; j <= m; j ++){//枚举体积
            for(int k = 0; k <= s[i]; k ++){
                if(j >=  k * v[i]){
                    f[i][j] = max(f[i][j], f[i - 1][j - k * v[i]] + k * w[i]);
                }
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

压缩新物品

打包压缩将一个物品的多个分成1个A,2个A，3个A·······这样存储新的物品，其实也是一种物品，也不过体积和价值也就跟着变成01背包问题，也就是背包问题的转化。

int cnt = 0;
    for(int i = 1; i <= n; i ++){
        int a, b, s;
        cin >> a >> b >> s;
        int k = 1;
        while(k <= s){
            cnt ++;
            v[cnt] = k * a;
            w[cnt] = k * b;
            s -= k;
            k *= 2;
        }
        if(s > 0){
            cnt ++;
            v[cnt] = s * a;
            w[cnt] = s * b;
        }
    }
    //多重背包转化为01背包问题
    for(int i = 1; i <= cnt; i ++){
        for(int j = m; j >= v[i]; j --){
            f[j] = max(f[j], f[j - v[i]] + w[i]);
        }
    }
    cout << f[m] << endl;
     return 0;

二进制优化

这种解法又叫做二进制优化，可不是二进制恋爱哦，周琳琳，方予可表示不背锅。

我们可以把十件物品A分成若干份，这若干份必须可以组合成0～10以内的任何一个数字。
做法是：1,2,4,…,2^(k-1),10-2k+1
即：10可以分为 1，2，4，3
显然这四个数字，可以组合成0～10以内的任何一个数字，如 8 = 1 + 4 + 3
每一份对应的体积和价值，用系数乘以1件物品的体积和价值。
这么做的好处，可以把时间复杂度从O(nm)降为O(m log n)，剩下的继续用01背包问题的解法求解
其实，这种思路又和之前的整数拆分一样，用二进制的数组和早晚能拼出来目的数

#include<iostream>
#include<algorithm>
#include<vector>
using namespace std;
const int N = 2010;
int f[N],n,m;
struct good{
    int w,v;
};
int main()
{
    cin>>n>>m;
    vector<good> Good;
    good tmp;
    //二进制处理
    for(int i = 1 ; i <= n ; i++ ){
        int v,w,s;
        cin>>v>>w>>s;
        for(int k = 1 ; k <= s ; k*=2 ){
            s-=k;
            Good.push_back({k*w,k*v});//能按照2的次数性存放的商品组
        }
        if(s>0) Good.push_back({s*w,s*v});//剩余的组成新商品量级
    }
    //01背包优化+二进制
    for(auto t : Good)
        for(int j = m ; j >= t.v ; j--)
            f[j] = max(f[j] , f[j-t.v]+t.w ); 
    cout<<f[m]<<endl;
    return 0;

}

滑动队列解法（max tough）

从代码发现第二种和第三种是一样的代码，虽然是那么写的，主要是还是思路，第三种强调是二进制优化，第二种目的是让大家有拆分打包的思想。
滑动队列是在传统的DP方程的基础上进行适当调整循环条件，并且结合滑动窗口的思路，如果想清楚原题，可以看之前的算法基础模板题那篇文章

实际上我们并不需要二维的dp数组，适当的调整循环条件，我们可以重复利用dp数组来保存上一轮的信息

我们令 dp[j] 表示容量为j的情况下，获得的最大价值
那么，针对每一类物品 i ，我们都更新一下 dp[m] --> dp[0] 的值，最后 dp[m] 就是一个全局最优值
dp[m] = max(dp[m], dp[m-v] + w, dp[m-2*v] + 2*w, dp[m-3*v] + 3*w, ...)
接下来，我们把 dp[0] --> dp[m] 写成下面这种形式
dp[0], dp[v],   dp[2*v],   dp[3*v],   ... , dp[k*v]
dp[1], dp[v+1], dp[2*v+1], dp[3*v+1], ... , dp[k*v+1]
dp[2], dp[v+2], dp[2*v+2], dp[3*v+2], ... , dp[k*v+2]
...
dp[j], dp[v+j], dp[2*v+j], dp[3*v+j], ... , dp[k*v+j]
显而易见，m 一定等于 k*v + j，其中  0 <= j < v
所以，我们可以把 dp 数组分成 j 个类，每一类中的值，都是在同类之间转换得到的
也就是说，dp[k*v+j] 只依赖于 { dp[j], dp[v+j], dp[2*v+j], dp[3*v+j], ... , dp[k*v+j] }

因为我们需要的是{ dp[j], dp[v+j], dp[2*v+j], dp[3*v+j], ... , dp[k*v+j] } 中的最大值，
可以通过维护一个单调队列来得到结果。这样的话，问题就变成了 j 个单调队列的问题

所以，我们可以得到
dp[j]    =     dp[j]
dp[j+v]  = max(dp[j] +  w,  dp[j+v])
dp[j+2v] = max(dp[j] + 2w,  dp[j+v] +  w, dp[j+2v])
dp[j+3v] = max(dp[j] + 3w,  dp[j+v] + 2w, dp[j+2v] + w, dp[j+3v])
...
但是，这个队列中前面的数，每次都会增加一个 w ，所以我们需要做一些转换
dp[j]    =     dp[j]
dp[j+v]  = max(dp[j], dp[j+v] - w) + w
dp[j+2v] = max(dp[j], dp[j+v] - w, dp[j+2v] - 2w) + 2w
dp[j+3v] = max(dp[j], dp[j+v] - w, dp[j+2v] - 2w, dp[j+3v] - 3w) + 3w
...
这样，每次入队的值是 dp[j+k*v] - k*w

j≡rmod(v)的f(i,j) 滑动窗口求最大值的实现，只需利用队列在队头维护一个最大值的单调递减单调队列即可，为了更新所有 i 阶段里的状态 f(i,j)，我们只需再额外枚举所有的余数 r 即可。

结合了完全背包的多重背包，是最优化时间的解法。
首先使用完全背包将能用的内存都用掉，并且将剩余的空间和此刻的价值存下来作为滑动窗口的数据值
然后用多重背包去限制，

第一种情况是多重背包自身提供的数量少于完全背包使用量，那么背包窗口就要滑动到适宜点，并且将剩下的空间返回来，作为其他商品窗口加入的空间和浮动剩余空间的补充，其中 r=jmodvir=jmodvi，也可以理解为完全背包下把当前物品选到不能再选后，剩下的余数
得到 f(i,r)=f(i−1,r)f(i,r)=f(i−1,r) 后，我们再利用完全背包优化思路往回倒推一遍
会惊奇的发现一个滑动窗口求最大值的模型，具体就是当前下标和该最大值的下标之间差了x个v，那么就要加上 x个w。

#include <iostream>
using namespace std;
const int N = 1010, M = 20010;
int n, m;
int v[N], w[N], s[N];
int f[N][M];
int q[M];//q[在r的基础上存放几个v]的体积
int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
    for (int i = 1; i <= n; ++ i) {
        for (int r = 0; r < v[i]; ++ r) {
            int hh = 0, tt = -1;
            for (int j = r; j <= m; j += v[i]) {
            //r作为剩余空间下，填充v[i]查看嫩添加的最大量，q[j占用体积]=队列
             while (hh <= tt && j - q[hh] > s[i] * v[i]) hh ++ ;
             /*最多存放数量
             如果q[hh]恰好等于r的话,j=s*v+r时,j-s*v=r,此时正好有s个物品
                q[hh]=j-s*v,如果有s+1个物品时,j=(s+1)*v+r-s*v=r+v,大于r,就
                超过了物品范围范围;r+2v同理,如果j=(s+2)+r是则正好有s件物品
                通过等式,如果j=(s+3)v+r则有s+1间物品,无法通过等式.
              */
             while (hh <= tt && f[i - 1][q[tt]] + (j - q[tt]) / v[i] * w[i] <= f[i - 1][j]) {
                    -- tt; 
//要是选择拿下i的话剩余体积以及自身价值与不拿此量的对比，要是过载那么这个窗口大小就不合适，
//所以要想左滑动
             }
                q[ ++ tt] = j;
        // 因为f[j]=max(g[j],g[j-v]+w,····)其中g[j]也是需要参与的,所以更新应放在前面
                f[i][j] = f[i - 1][q[hh]] + (j - q[hh]) / v[i] * w[i];
                //当前hh下能存放下i的数量去凑最大
            }
        }
    }
    cout << f[n][m] << endl;
    return 0;
}

一维优化可以使用拷贝数组写法

#include <iostream>
#include <cstring>

using namespace std;

const int N = 1010, M = 20010;

int n, m;
int v[N], w[N], s[N];
int f[M], g[M];
int q[M];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
    for (int i = 1; i <= n; ++ i)
    {
        memcpy(g, f, sizeof g);
        for (int r = 0; r < v[i]; ++ r) {
            int hh = 0, tt = -1;
            for (int j = r; j <= m; j += v[i]) {
                while (hh <= tt && j - q[hh] > s[i] * v[i]) hh ++ ;
                while (hh <= tt && g[q[tt]] + (j - q[tt]) / v[i] * w[i] <= g[j]) -- tt;
                q[ ++ tt] = j;
                f[j] = g[q[hh]] + (j - q[hh]) / v[i] * w[i];
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

花式背包问题

混合背包

开始提升难度的变形，但是思路还是那么的朴实无华
有 N 种物品和一个容量是 V 的背包。
物品一共有三类：
第一类物品只能用1次（01背包）；
第二类物品可以用无限次（完全背包）；
第三类物品最多只能用 si 次（多重背包）；
每种体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使物品体积总和不超过背包容量，且价值总和最大。
输出最大价值。
我们会发现这个题就是将刚才最简背包里的问题分类存放，固定次数01背包和多重背包就可以视作一类，但是要对数据进行处理，多重背包，就是多重的解法，只是在f[i][j]的结果max中多判断几次
对此都是用最优方法，反向一维，二进制优化

int main(){
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i] >> s[i];
     for (int i = 1; i <= n; ++ i) {
        //完全背包
        if (!s[i]) {
            for (int j = v[i]; j <= m; ++ j){
                f[j] = max(f[j], f[j - v[i]] + w[i]);
            }
        }
        else {
            //把多重背包用二进制优化这样就变成做多个01背包了
            if (s[i] == -1) s[i] = 1;
            for (int k = 1; k <= s[i]; k *= 2) {
                for (int j = m; j >= k * v[i]; -- j) {
                    f[j] = max(f[j], f[j - k * v[i]] + k * w[i]);
                }
                s[i] -= k;
            }
            if (s[i])
                for (int j = m; j >= s[i] * v[i]; -- j) {
                    f[j] = max(f[j], f[j - s[i] * v[i]] + s[i] * w[i]);
                }
            }
        }
    }
    cout << f[m] << endl;
    return 0;
}

二维费用背包

在01背包的基础上加了额外条件，就是咱自己的背包不仅要求容量的上限，也要要求重量的上限。
我们会发现这里比01背包问题多了一个重量，所以我们只需要将 f[i][j] 变成 f[i][j][k] 就行了。

状态表示——集合：f[i][j][k] 表示考虑前 i个物品，且容量不超过 j，总重量不超过 k 的集合下能获得的最大价值。
状态表示——属性：因为是求最大价值，故为 max。
状态计算——集合划分：考虑第 i个物品选不选。
不选或选不了（剩余时间不够 j<v[i]）：f[i−1][j][k]。
选：f[i−1][j−v1[i]][k−v2[i]]+w[i]。首先你对第i个物品进行了你的抉择，所以前一维变成了 i−1，接着因为使用了 v1[i]的体积，所以应该是j−v[i]，使用了 v2[i]的重量所以是 k−v2[i]。最后你要把它带来的价值加上，所以要加上 w[i]。

#include<bits/stdc++.h>
using namespace std;
const int N=1e3+10;
int f[N][N];
int vol[N],weight[N],value[N];
int main(){
    int n,v,w;
    cin>>n>>v>>w;
    for(int i=1;i<=n;i++)cin>>vol[i]>>weight[i]>>value[i];
    for(int i=1;i<=n;i++){
        for(int j=v;j>=vol[i];j--){
            for(int k=w;k>=weight[i];k--){
                f[j][k]=max(f[j][k],f[j-vol[i]][k-weight[i]]+value[i]);
            }
        }
    }
    cout<<f[v][w]<<endl;
    return 0;
}

分组背包

有 N 组物品和一个容量是 V 的背包。
每组物品有若干个，同一组内的物品最多只能选一个。
每件物品的体积是 vij，价值是 wij，其中 i 是组号，j 是组内编号。
求解将哪些物品装入背包，可使物品总体积不超过背包容量，且总价值最大。
输出最大价值。
直接DP表
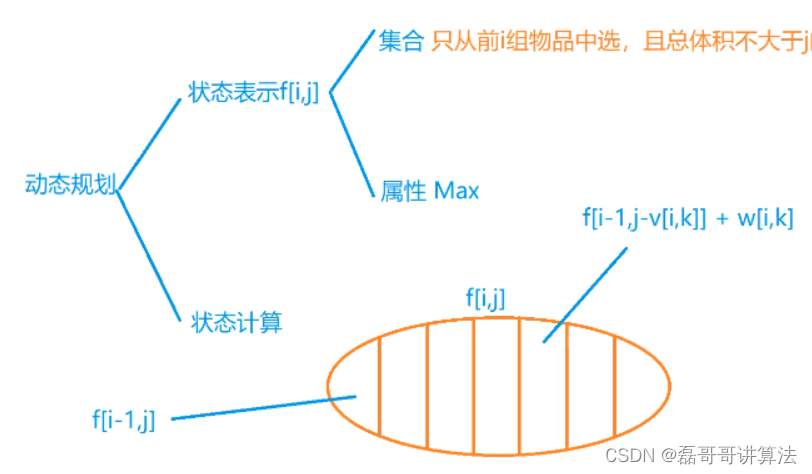
在这里插入图片描述
这里的思维分为两部分，一部分是对数据存储的分组操作。
其实就是因为分组使得基础数据从一维变成二维数组，但是还是基础的01背包

#include<bits/stdc++.h>
using namespace std;
const int N=110;
int f[N];
int v[N][N],w[N][N],s[N];
int n,m,k;
int main(){
    cin>>n>>m;
    for(int i=0;i<n;i++){
        cin>>s[i];
        for(int j=0;j<s[i];j++){
            cin>>v[i][j]>>w[i][j];
        }
    }

    for(int i=0;i<n;i++){
        for(int j=m;j>=0;j--){
            for(int k=0;k<s[i];k++){    //for(int k=s[i];k>=1;k--)也可以
                if(j>=v[i][k])     f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);  
            }
        }
    }
    cout<<f[m]<<endl;
}

依赖背包

有 N 个物品和一个容量是 V 的背包。
物品之间具有依赖关系，且依赖关系组成一棵树的形状。如果选择一个物品，则必须选择它的父节点

有依赖的背包问题是指物品之间存在依赖关系，这种依赖关系可以用一棵树来表示，要是我们想要选择子节点就必须连同其父节点一块选。
我们可以把有依赖的背包问题看成是分组背包问题，每一个结点是看成是分组背包问题中的一个组，子节点的每一种选择我们都看作是组内的一种物品，因此我们可以通过分组背包的思想去写。
但它的难点在于如何去遍历子节点的每一种选择，即组内的物品，我们的做法是从叶子结点开始往根节点做，并使用数组表示的邻接表来存贮每个结点的父子关系。

需要借助之前图论和算法基础模板里的基础模板，加速理解代码
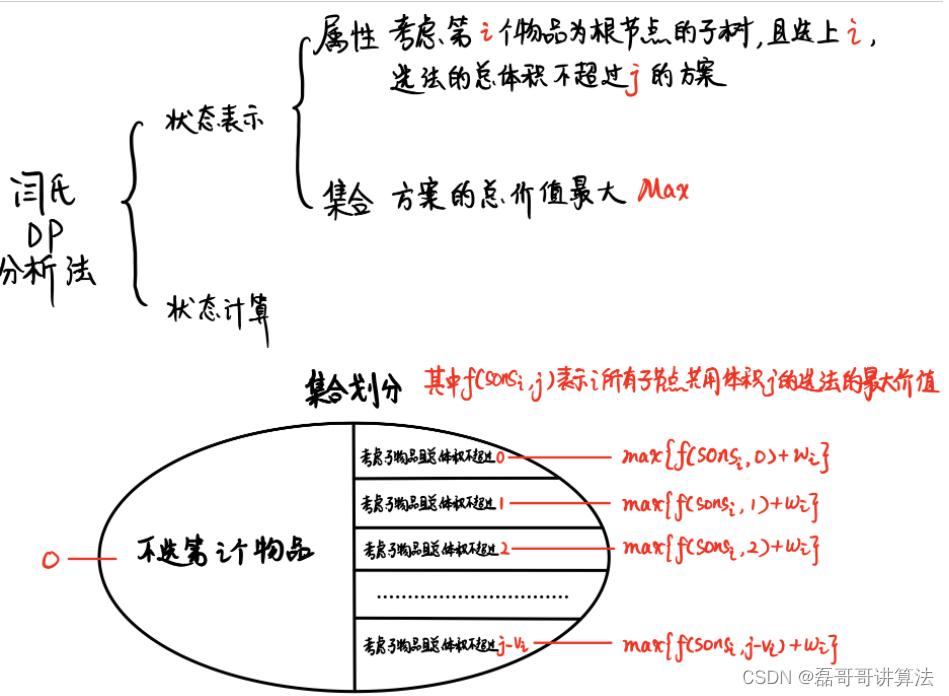
在这里插入图片描述

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N = 110;
int n,m;
int h[N],e[N],ne[N],idx;
/*h数组是邻接表的头它的下表是当前节点的标号，值是当前结点第一条边的编号（其实是最后加入的那一条边），e数组是边的集合，它的下标是当前边的编号，数值是当前边的终点；
ne是nextedge，如果ne是-1表示当前结点没有下一条边，ne的下标是当前边的编号，数值是当前结点的下一条边的编号，idx用于保存每一条边的上一条边的编号。
这样我们就知道了当前结点的第一条边是几，这个边的终点是那个结点，该节点的下一条边编号是几，那么邻接表就完成了
*/ 
int v[N],w[N],f[N][N]; 

void add(int a,int b){
    e[idx] = b,ne[idx] = h[a],h[a] = idx++;//该方法同于向有向图中加入一条边，这条边的起点是a，终点是b，加入的这条边编号为idx 
}

void dfs(int u){
    for(int i = h[u];i!=-1;i = ne[i]){//对当前结点的边进行遍历 
        int son = e[i];//e数组的值是当前边的终点，即儿子结点 
        dfs(son); 
        for(int j = m-v[u];j>=0;j--){
        //遍历背包的容积，因为我们是要遍历其子节点，所以当前节点我们是默认选择的。
        //这个时候当前结点我们看成是分组背包中的一个组，子节点的每一种选择我们都看作是组内一种物品，所以是从大到小遍历。
        //我们每一次都默认选择当前结点，因为到最后根节点是必选的。 
            for(int k = 0;k<=j;k++){//去遍历子节点的组合 
                f[u][j] = max(f[u][j],f[u][j-k]+f[son][k]);
            }
        }
    }
    //加上刚刚默认选择的父节点价值
    for(int i = m;i>=v[u];i--){
        f[u][i] = f[u][i-v[u]]+w[u];
    }
    //因为我们是从叶子结点开始往上做，所以如果背包容积不如当前物品的体积大，那就不能选择当前结点及其子节点，因此赋值为零 
    for(int i = 0;i<v[u];i++){
        f[u][i] = 0;
    }
}

int main(){
    memset(h,-1,sizeof h);
    cin>>n>>m;
    int root;
    for(int i = 1;i<=n;i++){
        int p;
        cin>>v[i]>>w[i]>>p;
        if(p==-1){
            root = i;
        }else{
            add(p,i);//如果不是根节点就加入邻接表,其中p是该节点的父节点，i是当前是第几个节点
        }
    }
    dfs(root);
    cout<<f[root][m]<<endl;
    return 0;
}

背包方案数

朴素解法

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出最优选法的方案数。注意答案可能很大，请输出答案模 109+7 的结果。

在选出最优结果的时候，加上路径跟踪的操作。
在这里插入图片描述
也就是将求结果的过程又反推了一次，并且将数据还原，如果有路径不同的再加和呈现总策划数。

for (int i = 1; i <= n; ++ i)  {
        for (int j = 0; j <= m; ++ j) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    }//理解成在知道y的情况求多个x合能构成y的情况，和数字划分是一样的思路
    g[0][0] = 1;
    for (int i = 1; i <= n; ++ i){
        for (int j = 0; j <= m; ++ j){
            if (f[i][j] == f[i - 1][j])
                g[i][j] = (g[i][j] + g[i - 1][j]) % mod;
            if (j >= v[i] && f[i][j] == f[i - 1][j - v[i]] + w[i])
                g[i][j] = (g[i][j] + g[i - 1][j - v[i]]) % mod;
        }
    }
    int res = 0;
    for (int j = 0; j <= m; ++ j){
        if (f[n][j] == f[n][m]){
            res = (res + g[n][j]) % mod;
        }
    }
    cout << res << endl;
    return 0;

记忆化搜索解法

若将背包中的状态看成一棵最短路树，则可以在这棵树的节点上同时保存到达这个节点的方案，
符合记忆化搜索的要求，可以直接取用。
不超过即至多，意思为容纳了体积小于背包容量的方案，解决方法有二：
一、同时搜索价值相等、体积偏小的方案，最后累计。
二、将背包取前 0 个物品，体积不超过 V 的所有状态的方案数置为 1，从而在搜索时钻空子，变相解决。

#include <bits/stdc++.h>
using namespace std;
const int N = 1010, mod = 1e9 + 7;
int n, m;
int v[N], w[N];
int f[N][N], g[N][N];
int dfs(int u, int c){
    if (!u) return g[u][c] = 1;
    if (g[u][c]) return g[u][c];
    if (f[u][c] == f[u - 1][c]) 
        g[u][c] = (g[u][c] + dfs(u - 1, c)) % mod;
    if (c >= v[u] && f[u - 1][c - v[u]] + w[u] == f[u][c]) 
        g[u][c] = (g[u][c] + dfs(u - 1, c - v[u])) % mod;
    return g[u][c];
}
int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 1; i <= n; i ++ ) scanf("%d %d", &v[i], &w[i]);
    for (int i = 1; i <= n; ++ i)
        for (int j = 0; j <= m; ++ j) {
            f[i][j] = f[i - 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i - 1][j - v[i]] + w[i]);
        }
    printf("%d", dfs(n, m));
}

背包具体方案

有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。
第 i 件物品的体积是 vi，价值是 wi。
求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。
输出字典序最小的方案。这里的字典序是指：所选物品的编号所构成的序列。物品的编号范围是 1…N。

朴素解法

背包输出方案也就是目标状态倒推回到初始状态的路径

#include <iostream>

using namespace std;

const int N = 1010;

int n, m;
int w[N], v[N];
int f[N][N];
int path[N], cnt;

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; ++ i) cin >> v[i] >> w[i];
    for (int i = n; i >= 1; -- i)
    {
        for (int j = 0; j <= m; ++ j)
        {
            f[i][j] = f[i + 1][j];
            if (j >= v[i]) f[i][j] = max(f[i][j], f[i + 1][j - v[i]] + w[i]);
        }
    }
    for (int i = 1, j = m; i <= n; ++ i)
    {
        if (j >= v[i] && f[i][j] == f[i + 1][j - v[i]] + w[i])
        {
            path[cnt ++ ] = i;
            j -= v[i];
        }
    }
    for (int i = 0; i < cnt; ++ i) cout << path[i] << " ";
    cout << endl;
    return 0;
}

递归解法

由于是字典序我们要从前往后来判断每个物品是否选择物品
状态表示：dp[i][j]表示从第i件物品到最后一件物品，体积不超过j所能装的最大价值
way[i][j]表示从第i件物品到最后一件物品，体积不超j的最优方案中所选的第一个物品编号
阶段划分：物品种数
转移方程：dp[i][j] = max(dp[i+1][j-v[i]]+w[i],dp[i+1][j]) 第一种是需要在j >= v[i]的时候成立
由于我们要尽可能的选择第i件物品，那么当dp[i + 1][j - v[i]] + w[i] >= dp[i][j]时我们就要将way[i][j] = i;
边界： dp[N + 1][0] = 0;


#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;
const int N = 1e3 + 10;
int dp[N][N],n,m;
int v[N],w[N];
int way[N][N];
//输出方案
void print(int x,int y)
{
    if(x == n + 1) return;
    int k = way[x][y];
    //判断是否选择了第x件物品
    if(k) cout<<k<<' ';//在递归函数的上面为由根节点到叶子节点进行操作
    print(x+1,y-v[k]);
    //在递归函数的下面进行操作，为叶子节点遍历完了，回溯由子节点到根节点进行操作

}
int main(void)
{
    cin>>n>>m;
    for(int i = 1;i<=n;i++) cin>>v[i]>>w[i];

    for(int i = n ;i>=1;i--)//注意计算当前阶段的状态需要之前的转态已经计算过了
        for(int j = 1;j<=m;j++) 
        {
            dp[i][j] = dp[i+1][j];
            if(j >= v[i])
            {
                if(dp[i][j] <= dp[i+1][j-v[i]] + w[i])//注意我们要尽可能的选择第i件物品，因为我们从前往后来判断是否选择物品
                {
                    dp[i][j] = dp[i+1][j-v[i]] + w[i];
                    way[i][j] = i;
                }
            }
        }

    print(1,m);
    return 0;
}

暴力解法

全保存路径

#include<iostream>
#include<vector>
using namespace std;
const int N=1001;

int v[N],w[N],n,V,f[N];
vector<int> ans[N];
int main()
{
    cin>>n>>V;
    for(int i=1;i<=n;i++)   scanf("%d %d",&v[i],&w[i]);
    for(int i=1;i<=n;i++)
        for(int j=V;j>=v[i];j--)
        {
            if(f[j]<f[j-v[i]]+w[i])
            {
                ans[j]=ans[j-v[i]];     //复制方案
                ans[j].push_back(i);    //更新方案
                f[j]=f[j-v[i]]+w[i];
            }
            else if(f[j]==f[j-v[i]]+w[i])
            {
                vector<int> b=ans[j-v[i]];b.push_back(i);
                if(b<ans[j])  ans[j]=b; //更新方案
            }
        }
    for(int i=0;i<ans[V].size();i++)    //输出方案
        cout<<ans[V][i]<<' ';
    return 0;
}

结论

背包问题的11种变形解题思路和基础模板题都呈现了出来，留意他们之间的变形关系，有的是几种背包一起用，也有的是维度的增加，或者路径的返回，背包DP是DP题海里的基础，还是需要多做积累和练习。
That is all

磊哥哥讲算法

关注

1
点赞
踩
3

收藏

觉得还不错? 一键收藏
打赏
2
评论
背包问题十一讲（你的背包，背到现在还没会））

背包DP问题变形11讲，论如何将01背包问题变成大家都不会做的样子有 N 件物品和一个容量是 V 的背包。每件物品只能使用一次。第 i 件物品的体积是 vi，价值是 wi。求解将哪些物品装入背包，可使这些物品的总体积不超过背包容量，且总价值最大。输出最大价值也就是n–循环存数据然后进行DP的存放，取到最大值，并且要求是每种物品只能用一次，体积不能超。在DP 的时候有可能我不一定塞满，但是我就是整到了最大价值了，这些都是伏笔，等会要考的哦。基本数据定义，之后都内定会有，在下面的变形里就不重复了...
复制链接

扫一扫