红黑树，B-/B+树代码实现增删算和原理拆分

前言

作为查找和树型数据结构的关联点，主要掌握B树，和B-树是一回事，但是B+树是另一种表达方式

红黑树

红黑交织，根和终结点是黑色，叶节点默认是最后查找失败null，作为叶节点，构建方式了解即可

B树- or null

文字叙述定理

#include<iostream>
#include<bits/stdc++.h>
using namespace std;
struct Node {
	int keys[4];//最多4个值，元素类型得一样
	struct Node* child[5];//最多5个指针
	int num;//这个比二叉树多一行，记录该节点具体有几个关键字，因为不一定是满的，比如头结点往往就1个值
};
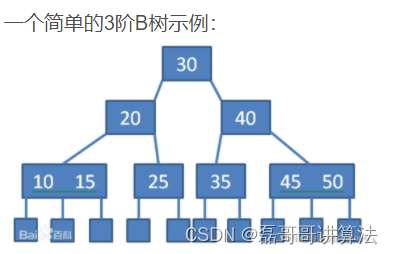
/*b树多路平衡查找树，孩子个数最大的树叫做b树的阶
树中的每一个结点至多有m棵子树,至多含有m-1个关键字
若根结点不是终端结点，则至少有两棵子树
非叶节点至少有上取整m/2棵子树，那么就是至少含有（上取整m/2）-1个关键字，
也就是关键字的缝隙中穿插着子树
所有叶节点都出现在同一个层次，也就是失败点，又称做外部结点
*/
/*属性类推包含n个关键字，高度为h，阶数为m的b树
* 因为每个b树中每个结点最多有m棵子树，m-1个关键字，所以高位h的m阶树
* n<=(m-1)*(1+m+m^2+*****m^h-1)=m^h -1
* 反解 h>=logm（n+1） 
* 所以每一个子树含有的关键字越少，其高度也就越高，b树第一层至少有一个结点
* 第二层至少有2个，除根结点外每个非终端结点至少有m/2上取整棵子树。
* 第三层至少有2[m/2]上取整个结点，对于关键字个数为n的b树，
* 叶节点查找不成功的结点为n+1，n+1>2*[m/2]^h-1,上取整，
* 解得 h<=log[m/2]（（（n+1）/2）+1）

空结点，被称为“失败节点”（就是待查找的数值不在这棵树上，一直找到空结点了，查找失败，因此得名）
对m叉查找树，其每个节点上有m个指针，m - 1个值，
查找的时候因为每个节点里面的数据是有序的，所以可以对每个节点里面也可以采用二分查找方法，
*/

B树的查找

在B树上进行查找与二叉查找树很相似，只是每个结点都是多个关键字的有序表，在每个结点上所做的不是两路分支决定，而是根据该结点的子树所作的多路分支决定。

B树的查找包含两个基本操作：
① 在B树中找结点；
② 在结点内找关键字。
 在B树上找到某个结点后，先在有序表中进行查找，若找到则查找成功，否则按照对应的指针信息到所指的子树中去查找。查找到叶结点时（对应指针为空指针），则说明树中没有对应的关键字，查找失败。
注意每个结点的下的空指针是关键字+1

B树的插入

与二叉查找树的插入操作相比，B树的插入操作要复杂的多。
在二叉查找树中，仅需要查找到需插入的终端结点的位置。但是，在B树中找到插入位置后，并不能简单地将其添加到终端结点中，因为此时可能会导致整棵树不再满足B树定义中地要求。

将关键字key插入到B树的过程如下：

• 定位。利用B树查找算法，找出插入该关键字的最低层中的某个非叶结点。
• 插入。在B树中，每个非失败结点的关键字的个数都在区间[ ⌈ m / 2 ⌉ − 1 , m − 1 ]内。
  插入后的结点关键字个数小于m mm，可以直接插入；
  插入后检查被插入结点内关键字的个数，当插入后的结点关键字个数大于m − 1 m-1m−1时，必须对结点进行分裂。

分裂的方法：
取一个新结点，在插入key后的原始结点，从中间位置将其关键字分为两部分：

• 左部分包含的关键字放在原始结点中；
• 右部分包含的关键字放在新结点中；
• 中间位置（⌈ m / 2 ⌉ \lceil m/2 \rceil⌈m/2⌉）的结点插入原结点的父结点。
• 若此时导致其父结点的关键字个数也超过了上限，则继续进行这种分裂操作，直至这个过程传到根结点为止，进而导致B树高度增加1。

B树的删除

B树的删除操作与插入操作类似，不过要稍微复杂一些，即要使得删除后的结点中的关键字个数，因此涉及到结点的合并问题。所以b树的删除有两种情况，且在b树这一系列题，默认向上取整

删除的关键字不在终端结点（最低层非叶结点）

• 当删除的关键字k不在终端结点的时候，若小于k的子树中关键字个数>[m/2]-1，则找到其先序结点取代然后再递归，观察是否有连锁反应
• 若大于k的子树中关键字个数>[m/2]-1，则找出后继值k，并替代之后递归删除。
• 若前后两个子树中的关键字个数均为[m/2]-1，那么就直接合并并删除k

删除的关键字在终端结点（最低层非叶结点）

当被删除的关键字再终端结点最底层非页结点

• 直接删除关键字，若删除关键字所在结点的关键字个数>[m/2]-1表明删除该关键字后仍然满足，所以就可以删除跑路
• 兄弟可以借用 若被删除的关键个数所在结点删除前的关键字个数=[m/2]-1且与此结点相邻的左右兄弟结点的关键字个数>=[m/2]-1，则需要调整该结点，将借来的关键码上移，然后将双亲结点中的关键码下移动
• 兄弟不可以借用 若被删除关键字所在结点删除前的关键字个数 = [m/2]-1，且此时与该结点相邻的右（左）兄弟结点的关键字个数 =[m/2]-1，则将关键字删除后与右（左）兄弟结点及双亲结点中的关键字进行合并。被删结点与兄弟结点合并成一个结点；并将双亲中它们所夹的关键码下移

代码实现

const int T = 2;					// 最小度
const int MIN_KEY = T - 1;
const int MAX_KEY = 2 * T - 1;
const int MIN_CHILD = MIN_KEY + 1;
const int MAX_CHILD = MAX_KEY + 1;	// 阶
typedef int keyType;				// 键值类型
// 节点类型
struct BNode {
	BNode(bool state = true, int num = 0) :keyNum(num), is_Leaf(state) {
		for (int i = 0; i < MAX_CHILD + 1; ++i)
			Child[i] = NULL;
	}
	keyType Key[MAX_KEY + 1];		// 键值域
	BNode* Child[MAX_CHILD + 1];	// 孩子
	int keyNum;		// 节点已存入键值数
	bool is_Leaf;	// 是否为叶子节点
};
// B-树
class BTree {
	friend bool insertFix(BTree& Tree, BNode* node, keyType key);
public:
	bool Insert(keyType key);	// 插入
	bool Delete(keyType key);	// 删除
	bool Search(keyType key);	// 查找
	void Traverse(BNode* node);	// 遍历
	BTree() :Root(NULL) {}
	BNode* Root;
};
// 查找
bool BTree::Search(keyType key) {
	if (NULL == Root) return false;
	BNode* T = Root;
	while (1) {
		int i = T->keyNum;
		if (T->is_Leaf) {
			while (i > 0 && T->Key[i - 1] > key) --i;
			if (T->Key[i - 1] == key) return true;
			return false;
		}
		else {
			while (i > 0 && T->Key[i - 1] > key) --i;
			if (T->Key[i - 1] == key) return true;
			T = T->Child[i];
		}
	}
}
// 分裂节点（ 分裂节点P的pos位置的子节点 ）
void splitNode(BNode* P, int pos, BNode* C) {
	BNode* LC = new BNode(C->is_Leaf, MIN_KEY);		// 新的左孩子
	BNode* RC = new BNode(C->is_Leaf, MIN_KEY + 1);	// 新的右孩子
	// 转移键值
	for (int i = 0; i < MIN_KEY; ++i) {
		LC->Key[i] = C->Key[i];
		RC->Key[i] = C->Key[MIN_KEY + 1 + i];
	}
	RC->Key[MIN_KEY] = C->Key[MAX_KEY];
	// 非叶子节点需要转移子树
	if (!C->is_Leaf) {
		for (int i = 0; i < MIN_CHILD; ++i) {
			LC->Child[i] = C->Child[i];
			RC->Child[i] = C->Child[MIN_CHILD + i];
		}
	}
	RC->Child[MIN_CHILD] = C->Child[MAX_CHILD];
	// 中间键值上移到父节点
	// 父节点pos位置后的键值和子树后移，腾个空位
	int i = P->keyNum;
	for (; i > pos; --i) {
		P->Key[i] = P->Key[i - 1];
		P->Child[i + 1] = P->Child[i];
	}
	P->Key[pos] = C->Key[MIN_KEY];		// 键值上移
	P->Child[i] = LC;
	P->Child[i + 1] = RC;
	++P->keyNum;
}
// 插入调整操作
bool insertFix(BTree& Tree, BNode* node, keyType key) {
	int i = node->keyNum;
	if (node->is_Leaf) {	//叶子节点
		while (i > 0 && node->Key[i - 1] > key) {
			node->Key[i] = node->Key[i - 1];	// 后移腾位
			--i;
		}
		node->Key[i] = key;
		++node->keyNum;
		if (node->keyNum == MAX_KEY + 1 && node == Tree.Root) {	// 插入树根位置 且树根已满
			BNode* newRoot = new BNode();	// 新的树根
			newRoot->is_Leaf = false;
			splitNode(newRoot, 0, node);
			Tree.Root = newRoot;
			return true;
		}
		else if (node->keyNum == MAX_KEY + 1) return true;	// 已满
		return false;
	}
	else {	 // 内节点
		while (i > 0 && node->Key[i - 1] > key) --i;
		int flat = insertFix(Tree, node->Child[i], key);
		if (flat) {		// 插入的子树已满
			splitNode(node, i, node->Child[i]);
		}
		if (node->keyNum == MAX_KEY + 1 && node == Tree.Root) {	// 内节点的树根已满
			BNode* newRoot = new BNode();	// 新的树根
			newRoot->is_Leaf = false;
			splitNode(newRoot, 0, node);
			Tree.Root = newRoot;
			return true;
		}
		else if (node->keyNum == MAX_KEY + 1) return true;
		return false;
	}
}
// 插入
bool BTree::Insert(keyType key) {
	if (Search(key)) return false;		// 已存在
	if (NULL == Root) {		// 空树
		Root = new BNode();
		Root->Key[Root->keyNum] = key;
		++Root->keyNum;
		return true;
	}
	insertFix(*this, Root, key);
	return true;
}
// 合并操作
void merge(BNode* P, int pos) {
	BNode* LC = P->Child[pos];
	BNode* RC = P->Child[pos + 1];
	LC->Key[LC->keyNum] = P->Key[pos];
	++LC->keyNum;
	for (int i = 0; i < RC->keyNum; ++i) {
		LC->Key[LC->keyNum + i] = RC->Key[i];
		++LC->keyNum;
	}
	for (int i = pos + 1; i < P->keyNum; ++i) {
		P->Key[i - 1] = P->Key[i];
		P->Child[i] = P->Child[i + 1];
	}
	--P->keyNum;
}
// 删除
bool BTree::Delete(keyType key) {
	if (NULL == Root || 0 == Root->keyNum) return false;
	BNode* T = Root;
	stack<BNode*> NODE;
	while (1) {
		NODE.push(T);
		int i = 0;
		while (i < T->keyNum && T->Key[i] < key) ++i;
		if (i < T->keyNum && T->Key[i] == key) {		// 删除键值在该节点中
			if (T->is_Leaf) {	// 叶子节点，删除
				for (; i < T->keyNum - 1; ++i) {
					T->Key[i] = T->Key[i + 1];
				}
				--T->keyNum;
				break;
			}
			else {	// 非叶子节点，找后继/也可以找前驱（必存在）
				BNode* RC = T->Child[i + 1];	// 右孩子
				while (!RC->is_Leaf) RC = RC->Child[0];
				T->Key[i] = RC->Key[0];
				key = RC->Key[0];
				T = T->Child[i + 1];
			}
		}
		else {		// 删除节点不在该节点中
			T = T->Child[i];
		}
	}
	// 删除后调整
	BNode* P = NODE.top();
	NODE.pop();
	while (!NODE.empty()) {
		T = P;
		P = NODE.top();
		NODE.pop();
		if (T->keyNum < MIN_KEY) {
			int i = 0;
			for (; i <= T->keyNum; ++i) {
				if (T == P->Child[i]) break;
			}
			BNode* LB = i > 0 ? P->Child[i - 1] : NULL;
			BNode* RB = i < P->keyNum ? P->Child[i + 1] : NULL;
			if (LB && LB->keyNum > MIN_KEY) {			// 左兄弟存在且键值富余
				for (int k = T->keyNum; k > 0; --k) {
					T->Key[k] = T->Key[k - 1];
				}
				T->Key[0] = P->Key[i - 1];
				++T->keyNum;
				P->Key[i - 1] = LB->Key[LB->keyNum - 1];
				--LB->keyNum;
			}
			else if (RB && RB->keyNum > MIN_KEY) {	// 右兄弟存在且键值富余
				T->Key[T->keyNum] = P->Key[i];
				++T->keyNum;
				P->Key[i] = RB->Key[0];
				for (int k = 0; k < RB->keyNum - 1; ++k) {
					RB->Key[k] = RB->Key[k + 1];
				}
				--RB->keyNum;
			}
			else if (LB) { // 左兄弟存在但不富余
				merge(P, i - 1);
				T = P->Child[i - 1];
			}
			else if (RB) {	// 右兄弟存在但不富余
				merge(P, i);
				T = P->Child[i];
			}
		}
	}
	// 树根被借走，树高 -1
	if (Root == P && P->keyNum == 0) {
		Root = P->Child[0];
	}
	return true;
}

B+树

考的比较少，了解的话跳转这个链接讲解和清楚
B+树详解拆解
可以对比理解的是，b+树会将关键字存放链接在一起，压扁之后就是单调数组
①数据项 只存储在树叶上。（数据项就是实实在在的数据，而不是索引）
②非叶子结点最多可以 存储 M个关键字(B树是M-1个)以指示搜索的方向(这里的关键字是指索引)。
这里的M个关键字是按从小到大的顺序排序的。M个关键字，就有M个指针，指向进一步查找的路径。
(有K个子节点就有K个索引,非叶子节点元素同时存在于叶子节点中,为其最大值或最小值)

伪代码讲解

查找

func find(<搜索码值> K) returns nodepointer  //给定一个搜索码值，找出它的叶子节点 returns nodepointer 定义返回值类型
return tree-search(root, K);   //从根开始搜索 返回 tree-search 
end func 

func tree-search(nodepointer, <搜索码值> K) returns nodepointer
//在树上搜索数据项
if  nodepointer 是叶子结点，返回nodepointer
else
       if K<K1, return  tree-search(P0, K); //非叶子节点的索引范围 ,P0对应最左端索引的子树  (i=1)
       else
              if  K≥Km, return  tree-search(Pm, K); // M= 非叶子节点包含的关键字(索引)/目录项数 ,Pm对应最右端索引的子树 (i=M)
       else
              找到满足Ki≤K＜Ki+1条件的i;// i取值1~M-1
              return  tree-search(Pi, K)
endfunc

增删

proc insert(nodepointer, entry, newchildentry)
// 把entry插入到根为“*nodepointer”的子树中； 
// “newchildentry”开始时是null，除非孩子被分裂，否则将已知返回null 
 
if nodepointer IS非叶子节点，new NodeP N=nodepointer， //N对应的非叶子节点定长M
       找到满足Ki≤entry的码值＜Ki+1 条件的i； //选择子树 
       insert(Pi, entry, newchildentry)；               //递归插入entry 选择Pi子树  找到叶子节点插入entry
       if newchildentry==null，return null；              //通常的情况；不分裂孩子 
       else //需要分裂，必须在N中插入*nodepointer  
            //找到叶子结点添加后 NodeP newchildentry  = <L2的最小值,指向L2最小值的指针>
              if  N有空间，                  //通常情况 
                     在N中放入*newchildentry ; 
                      newchildentry=null，return null；//重新赋值为null
              else   //注意与叶子页分裂的差别 
                     分裂N； //M个码值和M个节点指针 
                     前M/2个码值和M/2个节点指针留下； // Old NodeP
                     后M/2个码值和M/2个节点指针移入到新节点N2中， // new NodeP
                     //*nodepointer 父节点 用于N和N2之间的搜索 
                     newchildentry = &（<N2 上最小的码值，指向N2的指针>） 
                     if N. isRoot， 
                     分裂根节点,创建含有<指向N的指针，*nodepointer>的新节点；//新节点为<指向根节点N,N的值>
                     使树的根节点的指针指向新节点 //相当于复制了一份,作为子节点
                    return newchildentry；   
 
if nodepointer IS叶子节点，new NodeP L=nodepointer， //大概 NodeP L = new NodeP(nodepointer);
       if L有空间，//通常情况满足  L的大小为叶子节点可存储的数据项
              在L中放入entry ，设newchildentry为null, 并返回； 
       else，//偶尔，叶子是满的  此时newchildentry 
              分裂叶子结点L成左右两个叶子结点：前L/2个数据项留于L，//Old NodeP
                                           其余的移到新叶子节点L2中； //new NodeP
              newchildentry = &（<L2上最小的码值，指向L2的指针>）； //将第L/2+1个记录的K进位到父结点中
              设置L和L2链接指针； //维护叶子结点之间的链表结构
              return newchildentry； 
endproc

删除

proc delete(parentpointer, nodepointer, entry, oldchildentry) 
//把entry 从根为“nodepointer”的子树中删除； 
//“oldchildentry”开始时是null，除非孩子被删除，否则将一直返回为null 

if nodepointer 是非叶子节点，new NodeP N=nodepointer， 
       找到满足K i≤ entry 的关键值＜K i+1条件的i    //选择子树 
       delete(nodepointer, Pi, entry, oldchildentry);         //递归删除 找到叶子结点
       if oldchildentry ==null，return null；           // 通常的情况，不删除孩子 
       else                       //删除孩子节点 
              从N中移出  oldchildentry，  //接着，检查最小占用情况 
              if  N中有剩余的目录项，//通常情况 
                     oldchildentry=null，return null；  //删除不再继续 
              else，//注意叶子页合并的差别 
                     获得N的一个兄弟S；//利用parentpointer参数查找S 
                    if S有多余的数据项， 
                            通过父节点在N和S之间重新平均分布目录项； 
                            oldchildentry=null，return； 
                    else，合并N和S      //称作合并的节点M 
                            oldchildentry = &（父节点中指向M的当前目录项）； 
                            从父节点拉下分割码，并放在左侧节点上； 
                            把M中的所有目录项移到左侧节点； 
                            抛弃空节点M，return oldchildentry； 

  if nodepointer是叶子节点，new NodeP L=nodepointer
       if  L有剩余的目录项，//通常情况 L剩余数据项满足占有比率
              移出entry； oldchildentry=null； return； 
       else，           //偶尔，叶子的占有率过低 
       获得L的一个兄弟S；//利用父节点parentpointer 参数查找S 
       if  S有多余的目录项 
              通过父节点在L和S之间重新平均分布目录项； 
              //考虑S为左兄弟节点, L找到父节点中的关键字修改,考虑S为有兄弟节点时,S找到父节点对应关键字修改

              在父节点中找到指向右侧节点的目录项；//称为M  S,L靠右的称为M
              用M中新的最小码值代替父节点中的相应目录项中的码值; 
              oldchildentry=null，return； 
       else，合并L和S 成一个节点M //称作被合并的节点M  
              oldchildentry = & （父节点中指向M的当前数据项）； //
              把M中的所有数据项移到左侧节点； //数据项复制到 S,L中靠左的节点
              抛弃空节点M，调整叶子结点之间的指针，return oldchildentry；//维护链表结构
endproc

ennding report

hey girl you may be sad