DFT可以用向量形式表示

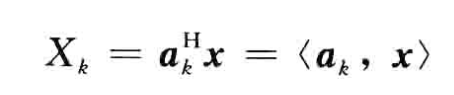
其第k个频率向量为

对DFT中任意两个频率向量做内积

可以得到结果

因此,DFT中各个频率向量是正交的,将频率向量归一化,即可构成正交基
假设我们有一个信号,那么在这组正交基下,这个信号可分解为各个投影向量之和

其中


上式理解为:观测数据向量可分解为N个正交的DFT频率向量之和
此三篇博客旨在理解频率向量、正交以及投影的基础概念,理解谱分解就是在正交基下的投影。后面将开始子空间的谱估计
DFT可以用向量形式表示

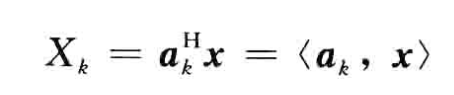
其第k个频率向量为

对DFT中任意两个频率向量做内积

可以得到结果

因此,DFT中各个频率向量是正交的,将频率向量归一化,即可构成正交基
假设我们有一个信号,那么在这组正交基下,这个信号可分解为各个投影向量之和

其中


上式理解为:观测数据向量可分解为N个正交的DFT频率向量之和
此三篇博客旨在理解频率向量、正交以及投影的基础概念,理解谱分解就是在正交基下的投影。后面将开始子空间的谱估计
 3034
3034

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


