维生素C吃多了会上火-个人CSDN博文目录
cs224w(图机器学习)2021冬季课程学习笔记集合
目录
1.思维大纲




2.链路
1.链路预测任务:回顾
任务是根据现有链接预测新链接
在测试时,对节点对(没有现有链接)进行排名,并预测前 𝐾 节点对
关键是为一对节点设计特征
2.链路预测任务的两种表述
- 随机丢失的链接:删除一组随机链接,然后旨在预测它们
- 随着时间的推移链接:给定𝐺[𝑡0,𝑡0′],输出预测在时间𝐺[𝑡1,𝑡1′]出现的边的排序列表L
3.基于相似性进行链路预测
方法:对于每对节点 (x,y) 计算分数 c(x,y)【例如,c(x,y) 可以是 x 和 y 的共同邻居的数量】,按递减分数 c(x,y) 对 (x,y) 进行排序,将前 n 对预测为新链接,查看这些链接中的哪些实际出现在𝐺[𝑡1,𝑡1′]
4.三种 特征化网络中两个节点之间关系的 描述符
a.Distance-based feature
两个节点之间的最短路径距离,然而这并没有捕捉到邻域重叠的程度
b.Local neighborhood overlap
捕获两个节点𝒗𝟏和𝒗𝟐之间共同邻居
Common neighbors:|𝑁 𝑣1 ∩𝑁 𝑣2 |
Jaccard系数
Adamic-Adar 指数
c.Global neighborhood overlap
Local neighborhood overlap,如果两个节点没有任何共同的邻居,度量值始终为零。但是,这两个节点将来可能仍可能连接。
Global neighborhood overlap通过考虑整个图来解决限制。
Katz 指标可以区分不同的邻居节点不同的影响力。Katz 指标给邻居节点赋予不同的权重, 对于短路径赋予较大的权重, 而长路径赋予较小的权重
Auv:矩阵A的Auv的值
Puv(K):节点u和v之间长度为K的路径的数量
Puv(k)=Akuv:点u和v之间长度为K的路径的数量,等于邻接矩阵A的k次幂的Auv的值
Sv1v2=
∑
l
=
1
∞
\sum_{l=1}^{\infty}
∑l=1∞
β
\beta
βl
A
A
Alv1v2
0<𝛽 <1: discount factor
𝛽会给比较长的距离以比较小的权重
Katz矩阵计算:
S
=
β
S=\beta
S=β
A
+
β
A+\beta
A+β2
A
A
A2
+
+
+
β
\beta
β3
A
A
A3
+
+
+
.
.
.
...
...
S
=
S=
S=
∑
i
=
1
∞
\sum_{i=1}^{\infty}
∑i=1∞
β
\beta
βi
A
A
Ai
−
(
I
−
β
-(I-\beta
−(I−β
A
)
A)
A)-1
−
I
-I
−I

3.图特征和图核
目标:我们想要表征整个图结构的特征
背景:kernels
kernels广泛用于传统的 ML 进行图级预测
想法:设计kernels而不是特征向量
内核简介:核函数(Kernels)
图内核:测量两个图之间的相似性
Graphlet Kernel
Weisfeiler-Lehman Kernel
1.graph kernal的关键思想
设计图特征向量𝜙(𝐺)
Bag-of-Words (BoW)
bag-of-words相当于是把文档表示成一个向量,每个元素代表对应word出现的概率,此处讲述的特征抽取方法也将图变成bag-of-something的形式,将图表示成一个向量,每个元素代表对应something出现的概率(这个something可以是node, degree)
2.Graphlet Kernel
a. g g gk:节点为k的其中一个图

b. f f fG = ( g =(g =(g1 , g ,g ,g2 , g ,g ,g3 , . . . , g n ) ,...,gn) ,...,gn) [ g [g [gi ] ∈ ]\in ]∈ G G G
表示在图 G G G中每个 g g gi出现的次数

c.graphlet kernel计算
𝐾 (𝐺,𝐺′) =𝒇𝐺T𝒇𝐺′
问题:如果 𝐺 和 𝐺′ 有不同的大小,这将极大地扭曲值
解决方案:对每个特征向量进行归一化
h
h
hG
=
f
=f
=fG
÷
\div
÷
S
u
m
(
f
Sum(f
Sum(fG
)
)
)
𝐾 (𝐺,𝐺′) =𝒉𝐺T𝒉𝐺′
d.graphlet kernel不足之处
计算量太大了
1.在具有n个节点的图中计算大小为K的graphlet,枚举需要nk次方
C
k
n
C_{k}^{n}
Ckn
≈
\approx
≈
n
n
nk
2.最坏的情况是不可避免的,因为子图同构测试(判断一个图是否是另一个图的子图)是 NP-hard[完全子图问题]
3.Weisfeiler-Lehman Kernel
目标:设计一个高效的图特征描述符𝜙(𝐺)
思路:利用邻域结构迭代,丰富节点词汇
算法:Color refinement
a.Color refinement[颜色细化]
- 为每个节点 𝑣 分配初始颜色 C C C(0) ( v ) (v) (v)
- 迭代地细化节点颜色:
C C C(k+1) ( v ) = (v)= (v)= H A S H ( { C HASH(\{C HASH({C(k) ( v ) , { C (v),\{C (v),{C(k) ( u ) } ) 其中 (u)\})其中 (u)})其中 u ∈ \in ∈ N ( v ) N(v) N(v)其中 HASH 将不同的输入映射到不同的颜色 - 经过𝐾颜色细化步骤, C C C(k+1) ( v ) (v) (v)总结了𝐾-hop邻域的结构
具体例子请参考课程
b.Weisfeiler-Lehman graph feature
进行K次迭代后,用整个迭代过程中颜色出现的次数作为𝜙(𝐺)
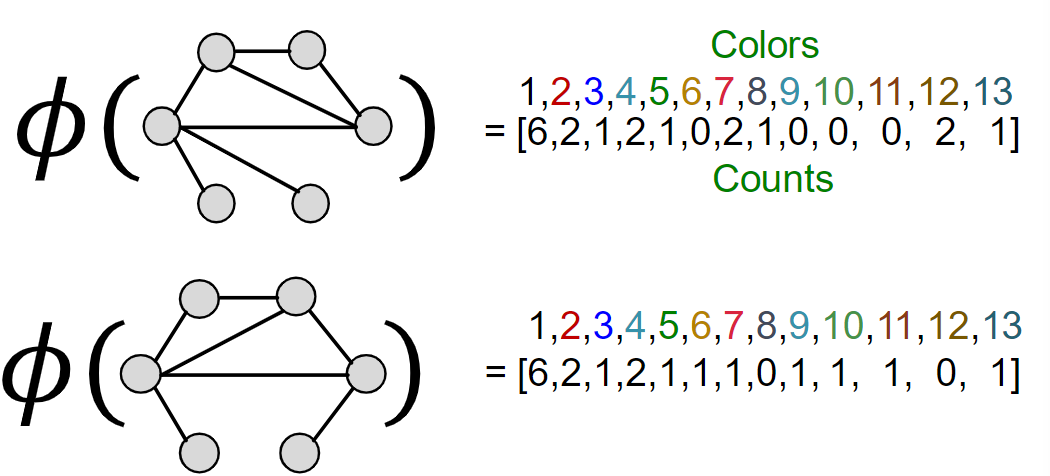
𝐾
(
𝐺
,
𝐺
′
)
=
𝐾(𝐺,𝐺′)=
K(G,G′)=𝜙(𝐺)𝜙(𝐺′)点积
c.Weisfeiler-Lehman Kernel优点
- WL 内核计算效率高,每一步颜色细化的时间复杂度线性的,因为它涉及聚合相邻颜色。
- 在计算内核值时,只需要跟踪两个图中出现的颜色,因此,最多是节点的总数。
- 计算颜色需要线性时间
- 总的来说,时间复杂度是线性的
4.Graphlet Kernel与Weisfeiler-Lehman Kernel比较
a.Graphlet Kernel
图表示是为Bag-of-graphlets
计算成本高
b.Weisfeiler-Lehman Kernel
应用
𝐾
−
s
t
e
p
𝐾-step
K−step颜色细化算法来丰富节点颜色
图表示是为Bag-of-color
计算高效
与图神经网络密切相关
4.总结
传统的机器学习管道
手工制作的特征 + ML 模型
图形数据的手工特征
Node-level:
节点度,节点中心性,聚类系数,graphlet
Link-level:
基于距离的特征,局部邻域重叠,全局邻域重叠
Graph-level::
Graphlet kernel, WL kernel























 2151
2151

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








