树状数组与线段树

一.树状数组

1.lowbit运算

lowbit(x) = x & (-x) 求能整除x的最大2的幂次的数。如6求出来是2。

2.树状数组需要解决的应用

先来看一个问题：

给出一个整数序列A，元素个数为N，接下来查询K次，每次查询将给出一个正整数x，求前x个整数之和

正常方法应该使用离线查询，即定义一个sum数组，sum[i]为前i个元素之和，直接查询sum[i]就行了了
【一般对一个操作多次使用就考虑能不能先把它列出来，不用每次计算】
现在我们将问题改成：

假设在查询的过程中随时可能给第x个整数加上一个整数v，要求在查询中能实时输出前x个整数之和。

现在发现离线查询不好使了，因为每次还需要更新sum[0],sum[1]…sum[i]时间复杂度很高，实时查询的话时间复杂度也不低，所以提出了树状数组。

3.树状数组

树状数组也是一个用来记录和的数组，只不过它存放的不是前i个整数之和，而是在i号位之前lowbit(i)个整数之和，即C[i]的覆盖长度（管辖范围）为lowbit(i)，如图：

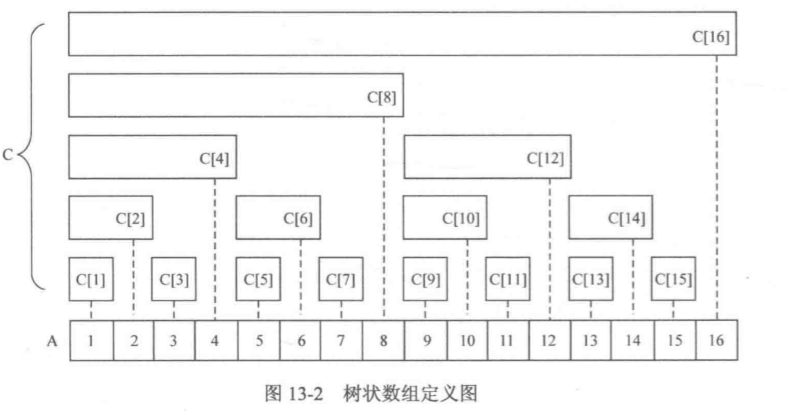
树状数组下标从1开始！！！
那么在这样的定义下，怎么解决下面两个问题来实现应用：
① 设计函数getSum(x)，返回前x个数之和A[i]+…+A[x]。
② 设计函数update(x,v)，实现将第x个数加上一个数v的功能，即A[x]+=v。

---

第一个问题：

我们知道C[x] = A[x-lowbit(x)+1]+…A[x]
于是可以得到

getSum(x) = A[1]+…A[x]
= A[1]+…+A[x-loxbit(x)] + A[x-lowbit(x)+1] +… +A[x]
= getSum(1,x-lowbit(x)) + C[x]

这样就非常容易得到getSum(x)函数：

int getSum(int x)
{
	int sum = 0;
	for(int i =x;i>0;i-=lowbit(i))
		sum += c[i];
	return sum;
}

可以看出getSum函数的时间复杂度为O(logn)。另外，如果要求数组下标在区间[x,y]内的数之和，可以转换成getSum(y)-getSum(x-1)。 ，即树状数组解决的问题是实时求区间和

---

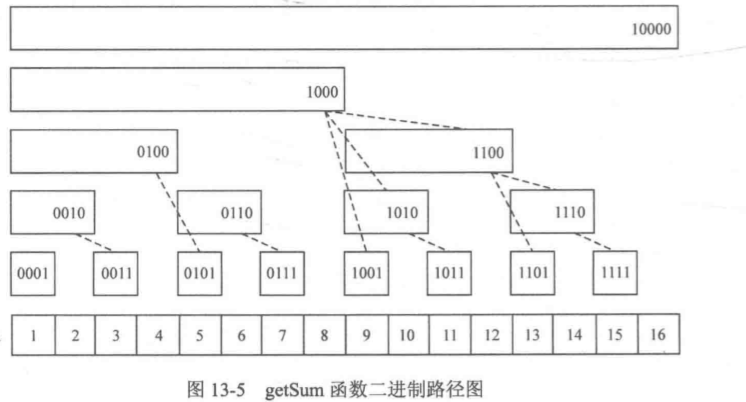
第二个问题：

就是要找到覆盖到A[i]的所有矩形，有图可知，要找到所有覆盖到A[i]的矩形，应该从第i个元素所在的矩形开始，向右找到最近的矩形，知道找完。
那怎么找到最近的矩形呢，有图中的面积关系可以知道，只要加上自己矩形面积的大小就得到了下一个矩形的位置，即

C[x] = C[x] + lowbit(x)

可以容易的得到update函数

void update(int x,int v)
{
	for(int i = x;i<=n;i+=lowbit(i))
	{
		C[i] += v;
	}
}

可以看出时间复杂度也是O(logn)

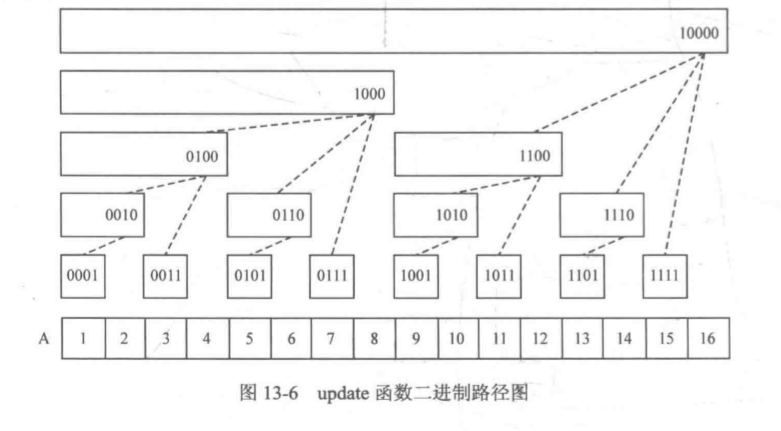
4.树状数组的经典应用——统计序列中在元素左边比该元素小的元素个数

具体问题如下：

给定一个有N个正整数的序列A，对序列中的每个数，求出序列中它左边比它小的数的个数。

先来看使用hash数组的做法，其中hash[x]记录整数x当前出现的次数。接着，从左到右遍历序列A，假设当前访问的是A[i],那么就令hash[A[i]]加1，表示当前整数A[i]的出现次数增加了一次；同时，序列中在A[i]左边比A[i]小的数的个数等于hash[i]+hash[2]…hash[A[i]-1]，这个和需要输出。但是很显然，这两个工作可以通过树状数组的update(A[i],1)和getSum(A[i]-1)
其实质就是将求区间和的问题转换成求散列数组的区间和转换成求普通数组比当前元素小的元素的个数

#define lowbit(i) ((i)&(-i))
int C[100];
int n;
int getSum(int x)
{
	int sum = 0;
	for (int i = x; i > 0; i -= lowbit(i))
		sum += C[i];
	return sum;
}
void update(int x, int v)
{
	for (int i = x; i <= n; i += lowbit(i))
	{
		C[i] += v;
	}
}

int main()
{
	cin >> n;
	for (int i = 1; i <= n; ++i)
	{
		int x;
		cin >> x;
		update(x, 1);
		cout << getSum(x - 1);
	}
	return 0;
}

---

我们再考虑一个问题

如果序列中数组非常散而且有的特别大，那开辟的树状数组不是浪费了空间吗，比如说A为{520,99999999,18,666,88888}。

其实如果只需要考虑到它们之间的大小关系，那么这个序列其实和{2,5,1,3,4}是等价的，同样的，序列{11,111,1,11}与{2,4,1,2}也是等价的。
一般来说，可以设置一个临时的结构体数组，用以存放输入的序列元素的值以及原始序号，而在输入完毕后将数组按val从小到大排序，排序完再按照“计算排名”的方式将“排名”根据原始序号pos存入一个新的数组即可，这种技巧称为离散化。

#define nmax 100
#define lowbit(i) ((i)&(-i))
int C[nmax];
int n;
typedef struct
{
	int index;
	int val;
}Node,NodeArray[nmax];
int getSum(int x)
{
	int sum = 0;
	for (int i = x; i > 0; i -= lowbit(i))
		sum += C[i];
	return sum;
}
void update(int x, int v)
{
	for (int i = x; i <= n; i += lowbit(i))
	{
		C[i] += v;
	}
}

bool cmp(Node a, Node b)
{
	return a.val< b.val;
}

int main()
{
	cin >> n;
	NodeArray node;
	for (int i = 1; i <= n; ++i)
	{
		cin >> node[i].val;
		node[i].index = i;
	}
	//离散化
	sort(node+1, node+1+ n, cmp);
	int tmp[nmax];
	for (int i = 1; i <= n; ++i)
	{
		if (node[i].val == node[i - 1].val)
			tmp[node[i].index] = tmp[node[i - 1].index];
		else
			tmp[node[i].index] = i;
	}
	//计算
	for (int i = 1; i <= n; ++i)
	{
		update(tmp[i], 1);
		cout << getSum(tmp[i]-1);
	}
	return 0;
}

一般来说，离散化只适用于离线查询，因为必须知道所以出现的元素之后才能方便进行离散化。

---

那么，如果给定一个二维整数矩阵A，怎样求A[1][1]~A[x][y]这个子矩阵所有元素之和，以及怎样给单点A[x][y]加上整数v？事实上只需把树状数组推广为二维即可。具体做法是，直接把update函数和getSum函数中的for循环改为两重。
另外，如果想求A[a][b]~A[x][y]这个子矩阵的元素之和，只需计算
getSum(x,y)-getSum(x-1,y)-getSum(x,y-1)+getSum(x-1,y-1)即可

---

另外，如果想单点查询和区间修改的话，就要更改树状数组的定义，由记录区间和变成记录这个区间加了多少，则相应的getSum和update要做改动

int  getSum(int x) {
	int sum = 0;
	for (int i = x; i < nmax; i += lowbit(i)) 
		sum += timeA[i];
	return sum;
}

void update(int x, int v) {
	for (int i = x; i > 0; i -= lowbit(i)) 
		timeA[i] += v;
}

二.线段树

上述介绍的树状数组是线段树的一个子集，由于事先简单比较常用，但是遇到一些更复杂的问题，比如说典型的动态区间求和问题，对整个区间做出操作等，就要使用线段树。

1.什么是线段树

线段树的主要思想是二分，也就是通过二分的方法来查找结点。首先看一下线段树的图表示

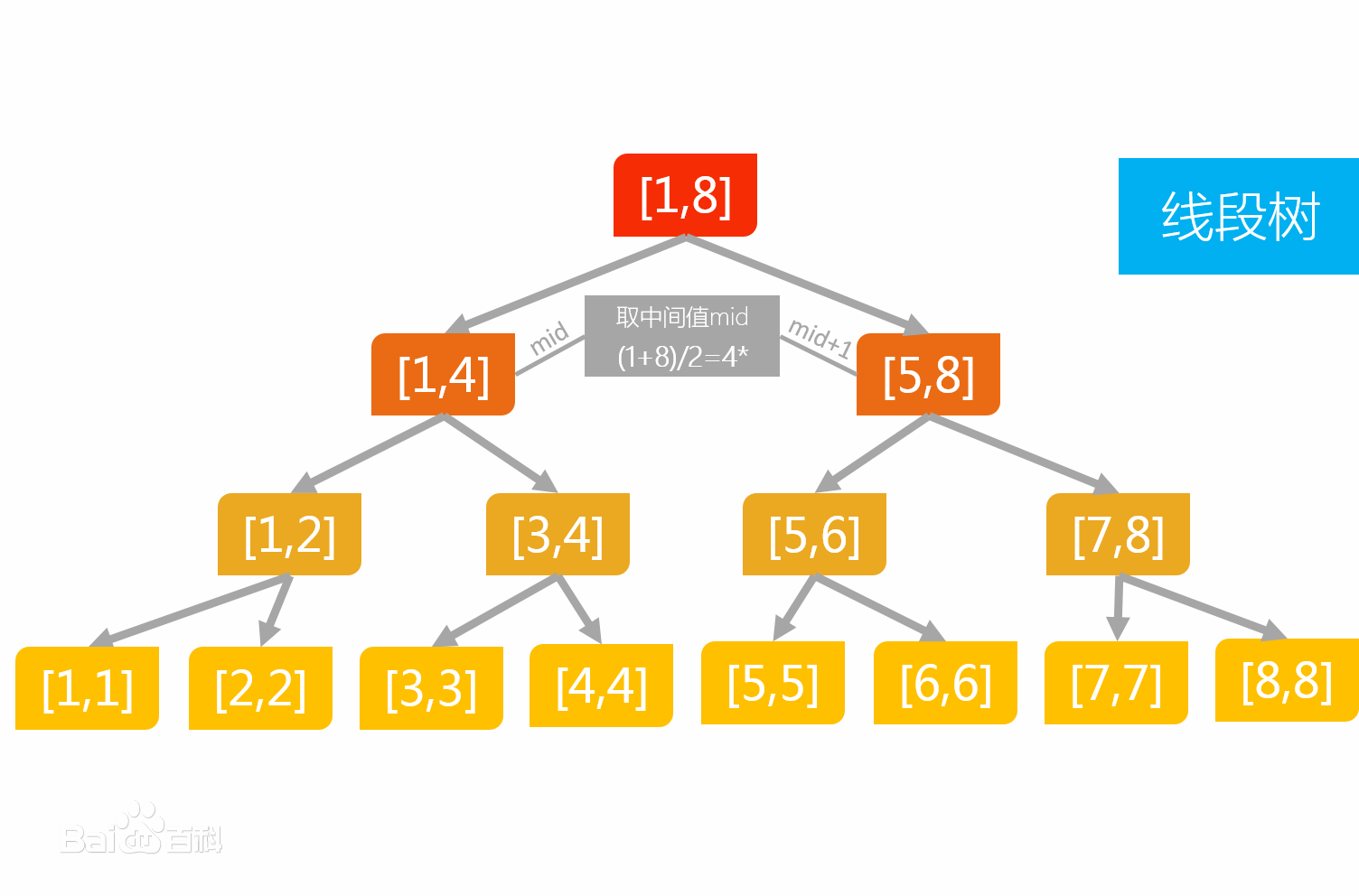
可以看到，非叶节点存储的是数据区间的和，而叶子结点则是数据具体的值

2.线段树之建树

由上述图可知线段树是非常消耗空间的，所以一般在数据量为n的情况下，用4n存储，并且存储方式同完全二叉树

#define nmax 1000
int tree[4 * nmax];
void init() {
	memset(tree, 0, sizeof(tree));
}
void build(int node, int low, int high) {
	if (low == high) {
		cin >> tree[node];
		return;
	}
	int mid = (low + high) / 2;
	build(node * 2, low, mid);
	build(node * 2+1, mid + 1,high);
	tree[node] = tree[node*2] + tree[node*2 + 1];
}

3.线段树操作之单点修改

单点更新非常类似二分查找，通过递归找到更新点的位置，在回溯的时候更新所有节点的值

void update(int n, int index, int low, int high, int node) {
	if (low == high) {
		tree[node]+=n;
		return;
	}
	int mid = (low + high) / 2;
	if (index <= mid)
		update(n, index, low, mid, node*2);
	else
		update(n, index, mid+1, high, node * 2+1);
	tree[node] = tree[node * 2] + tree[node * 2 + 1];
}

4.懒惰标记

在进行区间操作之前，要首先理解线段树的懒惰标记，试想，我们在操作的时候有可能有这样的操作。首先进行区间修改，修改了800次，然后再进行一次查询。这样，如果我们每次都将整个线段树的数据进行更新，实际上是非常慢的，如果我们能用一段空间，来记录修改数据，只有在使用的时候，一次性更新，就非常的方便。

所以这也是懒惰标记的作用**。可以先对修改的数据进行储存，只有在使用的时候才更新线段树。**那么，理论上我们应该建一个跟线段树同样大小的数组，称为懒惰数组，表示了每个节点的懒惰标记。有这样的操作：

1.修改数据的时候，每次递归到某节点，修改数据以后将数据的变化添加到数组中。

2.当使用到这个节点的时候，发现对应的懒惰标记存在，那么就应该更新该节点，以及以下的所有节点的数据，方便使用。

总之，就是不使用的时候就一直在积累，在使用的时候再统一更新。

void push_down(int node,int low,int high){
	if(lz[node]){
		int mid = (low+high)/2;
		lz[node*2] += lz[node];
		lz[node*2+1] += lz[node];
		tree[node*2] + 1LL*(mid-low+1)*lz[node];
		tree[node*2] += 1LL*(high-mid)*lz[node];
		lz[node] = 0;
	}	
}

5.线段树操作之区间更新

void update_range(int node,int l,int r,int low,int high,int add){
	if(l<=low && r>=R){
		lz[node] += 1LL * add;
		tree[node] += 1LL*(R-L+1)*add;
	}
	push_down(node,low,high);
	int mid = (low+right)/2;
	if(l<=mid)
		update_range(node*2,l,r,low,mid,add);
	if(r>=mid)
		update_range(node*2,l,r,mid+1,high,add);
	tree[node] = tree[node*2] + tree[node*2+1];
}

6.线段树操作之区间查找

int query_range(int node,int low,int high,int l,int r){
	if(l<=low && r>=high) 
		return tree[node];
	push_down(node,low,high);
	int mid = (low+high)/2;
	int sum = 0;
	if(mid >= low) 
		sum += query_range(node*2,low,mid,l,r);
	if(mid<high)
		sum += query_range(node*2+1,mid+1,high,l,r);
	return sum;
}