Benders decompostion2 解释+pythoncode(通过subdual求解)

已于 2023-02-06 11:12:39 修改
阅读量865 收藏 1
点赞数 1
文章标签： python 开发语言
于 2023-02-06 10:59:05 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_44149045/article/details/128897858
版权

1.关于benders decompostion的解释，请参考bender1，这里只简诉

  • 原问题

  • 限制性主问题（主）

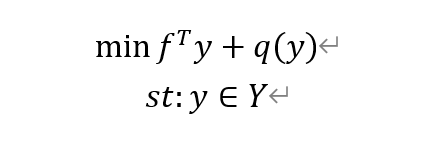
  • 子问题（子）

  • 对偶子问题（sub-dual）

  • 算法流程图

2. python代码

  • 算列解释-参考bender decompostion1


class bender:
    def __init__(self):
        self.y_num=5
        self.x_num=5
        self.fix_cost=[7 for i in range(self.y_num)]
        self.cost=[1,1,1,1,1]
        self.M = [[1,0,0,1,1],[0,1,0,0,1],[0,0,1,1,0]]
        self.b=[8,3,5]
        self.one_Matrix=list(np.identity(5))
        self.y_rhs=[8,3,5,5,3]
        #########关于master problem的参数#######
        self.q_LB=np.inf
        self.iter=0
        self.dual_Matrix=[[1,0,0,1,0,0,0,0],[0,1,0,0,1,0,0,0],[0,0,1,0,0,1,0,0],[1,0,1,0,0,0,1,0],[1,1,0,0,0,0,0,1]]

  • 整体流程：


##########################initialization############
mp=master_pro()
mp.optimize()
mp.display()
print('_++++++++++++++++++++++++_')
y_bar,q_bar=update_y_q(mp)
print('_++++++++++++++++++++++++_')
u,q_star,status=sub_dual(y_bar)
mp._sp_status = status
mp._q_star = q_star
mp._q_bar = q_bar
mp=bender_cut(mp,u)
mp.optimize()
mp.display()
y_bar,q_bar=update_y_q(mp)
# # #############start to loop################
while mp._iter<10:
    u,q_star,status=sub_dual(y_bar)
    print('***********sub_prob_q ',q_star)
    print('subdual_{}_\n_{}'.format(u,q_star))
    mp._sp_status = status
    mp._q_star = q_star
    mp._q_bar = q_bar  # q_LB
    if mp._q_star != mp._q_bar:
        new_mp = bender_cut(mp,u)
        new_mp.optimize()
        new_mp.display()
        y_bar,q_bar = update_y_q(new_mp)
        mp=new_mp
    else:
        break

  • 主问题

###############master model,但未添加cut
def master_pro():
    data = bender()
    # construct master problem
    mp = gp.Model('Master')
    mp._iter=0
    y = {}
    for i in range(data.y_num):
            y[i] = mp.addVar(lb=0,ub=1,vtype=GRB.BINARY, name="y" + str(i+1))
    q = mp.addVar(lb=0,ub=GRB.INFINITY,vtype=GRB.CONTINUOUS, name='q')  # q based on different value

    # set objective function
    obj = LinExpr(0)
    for i in range(data.y_num):
            obj.addTerms(data.fix_cost[i], y[i])
    obj+=q
    mp.setObjective(obj, GRB.MINIMIZE)
    #constraint
    # mp.addConstr(q>=0)
    mp.setParam('LazyConstraints', 1)
    mp._q=q
    mp._y=y
    mp.setParam('OutputFlag', 0)
    return mp

  • 更新y_bar和q_bar

#get y_bar
def update_y_q(model):
    y_bar = []
    q_bar=None
    for v in model.getVars():
        if 'y' in v.varName:
            y_bar.append(v.x)

        else:
            q_bar = v.x
    print('q_bar', q_bar)
    print('y_bar', y_bar)
        # print('jjjjjjjjjjjjjjjjj',y_bar)
    return y_bar,q_bar

  • 创建sub-dual问题，并找到对偶值u

  • extreme ray：当sub-dual unbounded时，用unbdRay，参数看代码块

  • extreme point：当sub-dual optimal时， 直接拿变量值

def sub_dual(y_bar):
    data=bender()
    sp=Model('Sub')
    a={}
    for i in range(3):
        a[i]=sp.addVar(vtype=GRB.CONTINUOUS,name='a'+str(i+1))
    beta={}
    for j in range(5):
        beta[j]=sp.addVar(lb= -1*GRB.INFINITY,ub=0,vtype=GRB.CONTINUOUS,name='beta'+str(j+1))
    #constraint:

    for i in range(5):
        sum=0
        for j in range(3):
            sum+=data.dual_Matrix[i][j]*a[j]
        for k in range(5):
            sum+=data.dual_Matrix[i][3+k]*beta[k]
        sp.addConstr(sum<=1)
        sum=0
    #objective
    OBJ=LinExpr(0)
    for i in range(3):
        OBJ.addTerms(data.b[i],a[i])
    for j in range(5):
        sum_obj=data.y_rhs[j]*y_bar[j]
        OBJ.addTerms(sum_obj,beta[j])
    sp.setObjective(OBJ,GRB.MAXIMIZE)
    sp.setParam('InfUnbdInfo' , 1)
    sp.setParam('OutputFlag', 0)
    sp.optimize()
    q_star=sp.objval
    sp.display()
    if sp.status==GRB.UNBOUNDED:
        u={}
        count=0
        for v in sp.getVars():
            u[count]=v.unbdRay
            count+=1
        print(u)
    elif sp.status==GRB.OPTIMAL:
        u={}
        count=0
        for v in sp.getVars():
            u[count]=v.x
            count += 1
        print(u)

    return u,q_star,sp.status

  • 添加cut

#callback
def bender_cut(model,u):
    print('______________')
    # if model._iter==0:
    #     print('iteration:', model._iter)
    #     model.addConstr(model._q>=0)
    #     model._iter+=1
    #     return model

    if model._iter >=0:
        data=bender()
        if model._sp_status==GRB.OPTIMAL:
            if abs(model._q_star-model._q_bar ) > 1e-6:
                print('~~~~~~~~~~~optimal~~~~~~~~~~~~~~~~~~')
                print('iteration:', model._iter)
                print('model._q_star',model._q_star)
                print('model._q_bar',model._q_bar)
                #add feasibility cut:
                lazy=LinExpr(0)
                sum=0
                for j in range(len(u)):
                    if j<3:
                        sum+=u[j]*data.b[j]
                    else:
                        coef=u[j]*data.y_rhs[j-3]
                        lazy.addTerms(coef,model._y[j-3])
                model.addConstr(lazy+sum<=model._q)###not sure q how to iter
                model._iter += 1
            else:
                model.terminate()

        elif model._sp_status == GRB.UNBOUNDED:
            print('~~~~~~~~~~~infeasible~~~~~~~~~~~~~~~~~~')
            print('iteration:', model._iter)
            lazy = LinExpr(0)
            sum = 0
            for j in range(len(u)):
                if j < 3:
                    sum +=np.dot(u[j],data.b[j])
                else:
                    coef = u[j] * data.y_rhs[j - 3]
                    lazy.addTerms(coef, model._y[j - 3])
            model.addConstr(lazy + sum <= 0)  ###not sure q how to iter
            model._iter += 1
        else:
            model.terminate()

        return model

  • 整体代码

import numpy as np
from gurobipy import *
import gurobipy as gp

class bender:
    def __init__(self):
        self.y_num=5
        self.x_num=5
        self.fix_cost=[7 for i in range(self.y_num)]
        self.cost=[1,1,1,1,1]
        self.M = [[1,0,0,1,1],[0,1,0,0,1],[0,0,1,1,0]]
        self.b=[8,3,5]
        self.one_Matrix=list(np.identity(5))
        self.y_rhs=[8,3,5,5,3]
        #########关于master problem的参数#######
        self.q_LB=np.inf
        self.iter=0
        self.dual_Matrix=[[1,0,0,1,0,0,0,0],[0,1,0,0,1,0,0,0],[0,0,1,0,0,1,0,0],[1,0,1,0,0,0,1,0],[1,1,0,0,0,0,0,1]]

###############master model,但未添加cut
def master_pro():
    data = bender()
    # construct master problem
    mp = gp.Model('Master')
    mp._iter=0
    y = {}
    for i in range(data.y_num):
            y[i] = mp.addVar(lb=0,ub=1,vtype=GRB.BINARY, name="y" + str(i+1))
    q = mp.addVar(lb=0,ub=GRB.INFINITY,vtype=GRB.CONTINUOUS, name='q')  # q based on different value

    # set objective function
    obj = LinExpr(0)
    for i in range(data.y_num):
            obj.addTerms(data.fix_cost[i], y[i])
    obj+=q
    mp.setObjective(obj, GRB.MINIMIZE)
    #constraint
    # mp.addConstr(q>=0)
    mp.setParam('LazyConstraints', 1)
    mp._q=q
    mp._y=y
    mp.setParam('OutputFlag', 0)
    return mp

#callback
def bender_cut(model,u):
    print('______________')
    # if model._iter==0:
    #     print('iteration:', model._iter)
    #     model.addConstr(model._q>=0)
    #     model._iter+=1
    #     return model

    if model._iter >=0:
        data=bender()
        if model._sp_status==GRB.OPTIMAL:
            if abs(model._q_star-model._q_bar ) > 1e-6:
                print('~~~~~~~~~~~optimal~~~~~~~~~~~~~~~~~~')
                print('iteration:', model._iter)
                print('model._q_star',model._q_star)
                print('model._q_bar',model._q_bar)
                #add feasibility cut:
                lazy=LinExpr(0)
                sum=0
                for j in range(len(u)):
                    if j<3:
                        sum+=u[j]*data.b[j]
                    else:
                        coef=u[j]*data.y_rhs[j-3]
                        lazy.addTerms(coef,model._y[j-3])
                model.addConstr(lazy+sum<=model._q)###not sure q how to iter
                model._iter += 1
            else:
                model.terminate()

        elif model._sp_status == GRB.UNBOUNDED:
            print('~~~~~~~~~~~infeasible~~~~~~~~~~~~~~~~~~')
            print('iteration:', model._iter)
            lazy = LinExpr(0)
            sum = 0
            for j in range(len(u)):
                if j < 3:
                    sum +=np.dot(u[j],data.b[j])
                else:
                    coef = u[j] * data.y_rhs[j - 3]
                    lazy.addTerms(coef, model._y[j - 3])
            model.addConstr(lazy + sum <= 0)  ###not sure q how to iter
            model._iter += 1
        else:
            model.terminate()

        return model


#get y_bar
def update_y_q(model):
    y_bar = []
    q_bar=None
    for v in model.getVars():
        if 'y' in v.varName:
            y_bar.append(v.x)

        else:
            q_bar = v.x
    print('q_bar', q_bar)
    print('y_bar', y_bar)
        # print('jjjjjjjjjjjjjjjjj',y_bar)
    return y_bar,q_bar

def sub_dual(y_bar):
    data=bender()
    sp=Model('Sub')
    a={}
    for i in range(3):
        a[i]=sp.addVar(vtype=GRB.CONTINUOUS,name='a'+str(i+1))
    beta={}
    for j in range(5):
        beta[j]=sp.addVar(lb= -1*GRB.INFINITY,ub=0,vtype=GRB.CONTINUOUS,name='beta'+str(j+1))
    #constraint:

    for i in range(5):
        sum=0
        for j in range(3):
            sum+=data.dual_Matrix[i][j]*a[j]
        for k in range(5):
            sum+=data.dual_Matrix[i][3+k]*beta[k]
        sp.addConstr(sum<=1)
        sum=0
    #objective
    OBJ=LinExpr(0)
    for i in range(3):
        OBJ.addTerms(data.b[i],a[i])
    for j in range(5):
        sum_obj=data.y_rhs[j]*y_bar[j]
        OBJ.addTerms(sum_obj,beta[j])
    sp.setObjective(OBJ,GRB.MAXIMIZE)
    sp.setParam('InfUnbdInfo' , 1)
    sp.setParam('OutputFlag', 0)
    sp.optimize()
    q_star=sp.objval
    sp.display()
    if sp.status==GRB.UNBOUNDED:
        u={}
        count=0
        for v in sp.getVars():
            u[count]=v.unbdRay
            count+=1
        print(u)
    elif sp.status==GRB.OPTIMAL:
        u={}
        count=0
        for v in sp.getVars():
            u[count]=v.x
            count += 1
        print(u)

    return u,q_star,sp.status

def dual_varible(model):
    if model.status==GRB.INFEASIBLE:
        u={}
        count=0
        for v in model.getVals():
            u[count]=v.unbdRay
        print(u)
    elif model.status==GRB.OPTIMAL:
        u={}
        count=0
        for v in model.getVars():
            u[count]=v.pi
        return u



##########################initialization############
mp=master_pro()
mp.optimize()
mp.display()
print('_++++++++++++++++++++++++_')
y_bar,q_bar=update_y_q(mp)
print('_++++++++++++++++++++++++_')
u,q_star,status=sub_dual(y_bar)
# u,q_star,status=sub(y_bar)
mp._sp_status = status
mp._q_star = q_star
mp._q_bar = q_bar
mp=bender_cut(mp,u)
# mp=bender_cut_dual(mp,u)
mp.optimize()
mp.display()
y_bar,q_bar=update_y_q(mp)
# # #############start to loop################
while mp._iter<10:
   
    u,q_star,status=sub_dual(y_bar)
    print('***********sub_prob_q ',q_star)
    print('subdual_{}_\n_{}'.format(u,q_star))
    mp._sp_status = status
    mp._q_star = q_star
    mp._q_bar = q_bar  # q_LB
    if mp._q_star != mp._q_bar:
        new_mp = bender_cut(mp,u)
        # new_mp = bender_cut_dual(mp, u)
        new_mp.optimize()
        new_mp.display()
        y_bar,q_bar = update_y_q(new_mp)
        mp=new_mp
    else:
        break

  • 最后结果展示

  • 主函数

  • 子函数

论文代码复现｜并行无人机的调度优化问题PDSTSP
梓潼的优化空间
02-12 6852
本文复现的是论文【1】的第二部分PDSTSP问题的求解：The flying sidekick traveling salesman problem: Optimization of drone-assisted parcel delivery - 百度学术 (baidu.com) 本文的代码复现参考了师兄的这篇帖子： 论文代码复现 | 无人机与卡车联合配送(Python+Gurobi)(The flying sidekick traveling salesman problem)_HsinglukL.
Gurobi如何关闭log输出信息，仅输出最优解信息
向阳小葵花的博客
12-02 6655
Gurobi的log信息十分详细，但有时我们只需要得到最终结果，并不需要观察其过程信息，这时就需要将Gurobi的og输出信息关闭掉。 这只需要使用Model.setParam设置一下model的OutputFlag参数，为0就是关闭，默认为1打开。 具体演示 如上图所示，gurobi有一大串输出的log信息。只需要在声明模型后，加入语句model.setParam('OutputFlag', 0)，再次运行模型。 model = Model('fenbo_model') model.se
手把手教你用Gurobi求解一个数学模型
旸的博客
11-26 2万+
手把手教你用Gurobi求解一个数学模型手把手教你用Gurobi求解一个数学模型带时间窗的车辆路径规划问题(Vrptw)python调用Gurobi求解Vrptw首先我们定义一下需要用到的参数：定义一个读取数据的函数，并对节点之间的距离进行计算：读取数据，并定义一些参数：调用gurobi进行模型的建立与求解：根据式(9)定义决策变量，并加入模型当中：根据式(1)定义目标函数，并加入模型当中：根据式(2)~(8)定义决策变量，并加入模型当中： 手把手教你用Gurobi求解一个数学模型 在接触Gurobi之前，
Benders分解算法详解
热门推荐
qq_42756072的博客
08-01 3万+
前言 最近在学习Benders Decomposition，看了不少的文章博客，但我感觉写的都不是很清楚，细节地方解释的也不够到位，于是就去读了英文论文原文，发现原文写的还是相当清楚的。本文也基于那篇论文，对Benders Decomposition进行总结。 背景 Benders Decomposition由Jacques F. Benders提出，用来求解混合整数规划问题(MIP:Mixed Integer Programming problem)，即同时包含整数和连续变量的极值问题，换句话说就是线性规
运筹系列50：使用JuMP进行Benders分解
kittyzc的博客
08-25 1387
1. Benders分解概述 benders decomposition的处理过程可以参考系列7，总的思路是把变量分为主问题变量和子问题变量，将子问题相关的目标函数和约束转化为对偶问题，子问题变量通过约束的形式不断进入主问题，因此整个问题变为：① 主问题求解 @ 子问题更新极点。benders分解要求子问题一定是线性问题，因此有一定局限性，如果不好处理的话，可以考虑求对偶问题，然后用列生成算法去求解。 有两种使用benders decomposition的方式，一种是使用lazy constraints，见
基于Benders分解算法的两阶段鲁棒优化求解及其MATLAB YALMIP+CPLEX实践
最新发布
05-12
接着，文章展示了如何利用Benders分解将复杂的问题分解为主问题和子问题分别求解，并通过不断的迭代和添加割平面约束逐步逼近最优解。文中还特别提到了一些实际操作中的技巧，如处理子问题不可行的情况以及如何调整...
Matlab 使用Benders分解法求解机组组合问题
10-07
在提供的文件“使用Benders分解法求解机组组合问题”中，应该包含了具体的Matlab代码示例，详细展示了如何设置和执行Benders分解过程。通过学习和理解这段代码，可以深入掌握Benders分解法在Matlab环境下的应用，并...
建模实战|第八期：Benders Decomposition求解设施选址问题(FLP)：理论及python代码实战
扎实耕耘，终有所获
09-10 1044
Benders Decompositions是一种用来解决有特殊结构问题的数学编程技术。它经常被用来解决大规模混合整数规划(mixed integer programming, MIP)问题。其主要思想是，将较复杂的模型分解成为2部分，分别求解2部分都较为容易，通过两部分之间的交互迭代，最终算法得到收敛，得到最优解。Master Problem主问题 - usually harder, MIP problem，一般是关于整数变量y的，是复杂变量的问题。
开源求解器SCIP的python接口学习手册
04-25
SCIP Python 接口学习手册 SCIP（Solving Constraint Integer Programs）是一个开源的数学优化求解器，用于解决混合整数规划问题。Python 是一种流行的编程语言， PySCIPOpt 是 SCIP 的 Python 接口，提供了一个...
pannel添加的子窗体很大_优化│TSP中两种不同消除子环路的方法及callback实现（Python调用Gurobi求解）...
weixin_39839968的博客
11-29 688
@TSP Model 1： `subtour-elimination` 消除子环路TSP整数规划模型Python调用Gurobi实现中的一些小问题TSP Model 2 ： MTZ约束消除子环路MTZ约束消除子环路为什么`MTZ`约束可以消除子环路？`callback`的工作逻辑: 王者荣耀版独家解读使用`callback`的通用步骤`callback`实现`subtour-elimination...
详解 Benders 分解与一个算例的 python 代码
天天向上的专栏
11-15 8535
听说过 benders 分解几年了，一直没有细看，最近论文里面也见到，还是有必要了解一下它的基本思想与用法的。
DW学习－Python基础04（列表）
木易是木易啊的博客
07-27 961
目录1 列表基础 1 列表基础 列表意义：索引对应值，索引从0开始，0代表第一个,-1代表最后一个。 定义：在[]内用逗号分开多个任意类型的值，一个值称为一个元素。 作用：按位置记录多个值，并且可以按照索引取指定位置的值。 取列表里的值：取的是某一个元素。 m=[1.1,"hello",["bingo",10],20] print(m) # [1.1, 'hello', ['bingo', 10], 20] print(m[2]) # ['bingo', 10] print(m[-1]) # 20 pr
大规模线性规划的对偶问题
HsinglukLiu的博客
08-08 2178
大规模线性规划的对偶问题大规模线性规划的对偶问题对偶理论简介SPP的对偶MCNF的对偶 大规模线性规划的对偶问题 对偶理论简介 SPP的对偶 MCNF的对偶
Python调用Gurobi：Assignment Problem(指派问题)简单案例
HsinglukLiu的博客
08-06 4844
Python调用Gurobi：简单案例Python调用Gurobi：简单案例Assignment Problem Python调用Gurobi：简单案例Assignment Problem from gurobipy import * import pandas as pd import numpy as np import random
Gurobi | 迭代中的参数变量/目标函数/约束修改
无运筹 不优化
05-04 5023
文章目录1.目标函数参数修改2.变量初始值赋值 1.目标函数参数修改 有时候会出现在迭代过程中需要修改目标函数参数的情况，例如在利用次梯度求解拉格朗日松弛对偶问题，我们不可能重新生成整个模型。 通过尝试发现以下方法可行，即在迭代中直接修改并重新生成目标函数。 from gurobipy import * m = Model('test') x = m.addVar(vtype=GRB.BINARY, name="x") y = m.addVar(vtype=GRB.BINARY, name="y")
两阶段鲁棒优化 | Bilinear 项的线性化
无运筹 不优化
08-02 3515
Bilinear 项的线性化
python中add_关于操作符：python的__add__ 和 __concat__有什么区别？
weixin_39995280的博客
11-26 751
python的标准操作符列表包括__add__(a, b)和__concat__(a, b)。它们通常都由a + b调用。我的问题是，他们之间有什么区别？有没有一个场景会使用一个而不是另一个？在一个对象上定义两个对象有什么原因吗？这是我在中找到方法的文档。编辑：增加了奇怪的是，这是文件：Finally, sequence types should implement addition (meani...
0 大规模MIP
HsinglukLiu的博客
08-08 985
大规模MIP大规模MIP的精确算法和实现：目录第1部分：CPLEX的Java API详解1. CPLEX简介2. 构建简单的模型3. CPLEX的高级应用第2部分：Gurobi的Python API详解1. Gurobi简介2. 构建简单的模型3. Gurobi的高级应用第3部分： 大规模MIP的常见精确算法及其实现相关概念凸包极射线LP, IP, QP, QCP, QCQP, SOCP的概念经典的MIP问题简介Assignment ProblemSPPTSPVRPMNF常用的高级建模技巧逻辑约束线性化技巧
python调用gurobi求解benders
05-02
要使用Gurobi求解Benders分解模型，首先需要在Python中安装Gurobi Optimizer，并使用Gurobi Python API编写代码。 以下是一个示例代码，展示了如何使用Gurobi Python API求解Benders分解模型： ```python import gurobipy as gp # 定义主问题 master = gp.Model("master") x = master.addVars(2, obj=[2, 3], vtype=gp.GRB.CONTINUOUS, name="x") master.addConstr(x[0] + x[1] <= 4, "c0") master.addConstr(x[0] - x[1] <= 1, "c1") # 定义子问题 subproblem = gp.Model("subproblem") y = subproblem.addVars(2, obj=[1, -1], vtype=gp.GRB.CONTINUOUS, name="y") subproblem.addConstr(y[0] + y[1] <= 2, "d0") # 定义Benders分解模型 benders = gp.Model("benders") benders.setParam('OutputFlag', 0) # 将主问题添加到Benders分解模型中 benders.setObjective(master.getObjective(), gp.GRB.MINIMIZE) benders.addVars(master.getVars(), lb=master.getVars(), ub=master.getVars(), obj=master.getVars()) # 添加子问题约束到Benders分解模型中 benders.addConstrs((y[i] == benders.getVarByName("x[" + str(i) + "]") for i in range(2)), "subproblem_constrs") # 解决Benders分解模型 benders.optimize() # 输出结果 print("Objective value: ", benders.ObjVal) print("x[0]: ", benders.getVarByName("x[0]").X) print("x[1]: ", benders.getVarByName("x[1]").X) ``` 在这个示例代码中，我们首先定义了一个主问题和一个子问题。主问题和子问题都是线性规划问题。然后，我们将主问题添加到Benders分解模型中，并将子问题约束添加到Benders分解模型中。最后，我们使用Benders分解模型求解问题，并输出结果。 需要注意的是，这只是一个简单的示例代码，实际的Benders分解模型可能更加复杂。因此，在实际应用中，需要根据具体问题编写代码。
评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值