引言
这个系列的三篇文章已经全部更新完成了
复数与正交信号完全指南(上)
复数与正交信号完全指南(中)
复数与正交信号完全指南(下)
本文翻译自 Richard Lyons 的 《A Quadrature Signals Tutorial: Complex, But Not Complicated》,这篇文章绘制了大量图片,对信号的复数表示进行图解。出于方便,文中图片将直接使用原文截图。在翻译的间隙中会插入一些本人的注解,用绿色字体表示,以作区分。
正交信号基于复数的概念,对于数字信号处理的新手而言,可能没有其他内容比这些数字及其奇怪的术语(如j-算子、复数、虚数、实数和正交)更让人感到头痛了。如果你对复数的物理意义和 j = − 1 j = \sqrt{-1} j=−1 算子感到困惑的话,不要难过,因为你并不孤单。毕竟,世界上伟大的数学家之一卡尔·高斯称j-算子为“阴影的阴影”(“shadow of shadows”)。本文将为试图为你带来希望,或许以后你就不必再为正交信号感到苦恼了。
正交信号处理在许多科学工程领域中都有应用,正交信号是描述现代数字通信系统的基石。 在本教程中,我们将——
- 先回顾复数的基础知识,并熟悉如何用它们来表示正交信号。
- 接下来,我们将学习负频率的概念,因为这涉及正交信号的代数符号,同时我们还要学习正交处理的语言。
- 此外,我们将使用三维时间和频率域图来赋予正交信号一些物理意义。
- 本教程最后简要介绍了如何通过正交采样生成正交信号。
为什么关心正交信号?
正交信号,也称为复数信号,被广泛用于许多数字信号处理应用中,例如:
- 数字通信系统,
- 雷达系统,
- 无线电测向方案中到达时间差处理,
- 相干脉冲测量系统,
- 天线波束形成应用,
- 单边带调制器,等等
这些应用属于正交处理的类别,它们通过相干检测(相干检测是一种信号解调机制,它利用调制信号的载波和接收到的已调信号相乘,然后通过低通滤波得到调制信号的检测方式)正弦信号的相位来进行更有效的信号处理,从而增强了处理信号的能力。
相干解调的一个案例是毫米波雷达,TI的这篇文章比较好的做了基础介绍,读者可以在完成本文阅读后再看这个案例,其中包括相干解调以及通过相位差进行速度检测。
正交信号是一个二维信号,其在某一时刻的值可以通过一个具有两部分的复数来指定:我们称之为实部和虚部。(尽管“实”和“虚”这两个词是传统的,但由于它们在我们的日常语言中的含义,通信工程师使用“同相”和“正交”这两个术语,稍后再详细讨论)先让我们回顾一下这些复数的数学符号。
复数的发展和表示法
为了建立我们的术语,我们将实数定义为我们在日常生活中使用的数字,例如电压、华氏温度或支票帐户余额。这些一维数字可以是正数,也可以是负数,如图 1(a) 所示。在该图中,我们展示了一个一维轴,单个实数可以由该轴上的点表示。出于传统,我们将该轴称为实轴。

图 1(b) 显示了一个复数 c,它也表示为一个点。然而,复数并不限于位于一维线上,而是可以位于二维平面上的任何位置。该平面称为复平面(一些数学家喜欢将其称为Argand diagram),它使我们能够表示具有实部和虚部的复数。例如,在图 1(b) 中,复数 c = 2.5 + j 2 c = 2.5 + j2 c=2.5+j2 是在复平面上既非实轴也非虚轴上的点。我们通过沿实轴移动 +2.5 个单位并沿虚轴向上移动 +2 个单位来定位点 c。这些实轴和虚轴就像地图上的东西南北一样。我们将从几何的角度来理解一些复数的运算。看一下图 2,我们可以使用直角三角形的三角学来定义表示复数 c 的几种不同方式。

复数 c 可以以多种不同的方式表示,例如:
| 符号名称 | 算数表达 | 说明 |
|---|---|---|
| 矩形形式 | c = a + b j c=a+bj c=a+bj | 用于解释目的。最容易理解(也称笛卡尔形式)。-------- (1) |
| 三角函数形式 | c = M [ c o s ( ϕ ) + j s i n ( ϕ ) ] c = M[cos(\phi) + jsin(\phi)] c=M[cos(ϕ)+jsin(ϕ)] | 通常用于描述通信系统中的正交信号。-------- (2) |
| 极坐标形式 | c = M e j ϕ c = Me^{j\phi} c=Mejϕ | 最令人费解,但却是数学中使用的主要形式(也称为指数形式,有时写为 M e x p ( j ϕ ) Mexp(j\phi) Mexp(jϕ))。-------- (3) |
| 幅度角形式 | c = M ∠ ϕ c=M\angle\phi c=M∠ϕ | 用于描述目的,但在代数方程中使用太麻烦(本质上是方程 Eq. (3). 的简写版本)。-------- (4) |
Eq.(3). 和 (4). 提醒我们,c 也可以被认为是复平面上相量的顶点,如图 2 所示,其幅度为 M,相对于正实轴有着
ϕ
\phi
ϕ 度的方向。请记住,c 是复数,变量 a、b、M 和
ϕ
\phi
ϕ 都是实数。 c 的大小,有时称为 c 的模,为:
M
=
∣
c
∣
=
a
2
+
b
2
(5)
M=|c|=\sqrt{a^{2}+b^{2}} \tag{5}
M=∣c∣=a2+b2(5)

回到正题。相角或幅角
ϕ
\phi
ϕ,是比值
虚部
实部
\frac{虚部}{实部}
实部虚部 的反正切,或:
ϕ
=
t
a
n
−
1
(
b
a
)
(6)
\phi = tan^{-1}(\frac{b}{a})\tag{6}
ϕ=tan−1(ab)(6)
如果把Eq.(3). 设为等于Eq.(2).,即
M
e
j
ϕ
=
M
[
c
o
s
(
ϕ
)
+
j
s
i
n
(
ϕ
)
]
Me^{j\phi} = M[cos(\phi) + jsin(\phi)]
Mejϕ=M[cos(ϕ)+jsin(ϕ)] ,我们就可以得到欧拉公式的表述之一:
e
j
ϕ
=
c
o
s
(
ϕ
)
+
j
s
i
n
(
ϕ
)
(7)
e^{j\phi} = cos(\phi) + jsin(\phi)\tag{7}
ejϕ=cos(ϕ)+jsin(ϕ)(7)
大多是书本中给出的都是欧拉公式的验证,只要分别将两边的自然指数函数和三角函数用泰勒级数展开,即可得出两边相等的结论,本文也不例外。但这并不是推导,只是验证。如果想更深入的理解欧拉公式,这篇文章可能是不错的材料。
读者现在应该会问:"为什么复数可以表示为一个以自然对数 e 为底的虚幂指数表达式呢?这很奇怪,但我们可以像欧拉一样,在图 3 第一行的 e z e^{z} ez 的级数展开定义中,将 j 插入 z 来验证 Eq.(7).。第二行显示了这一替换。接下来,我们对 j 的高阶项求值,得出图中第三行的数列。我们会发现,第三行中的交替项就是余弦函数和正弦函数的级数展开定义。
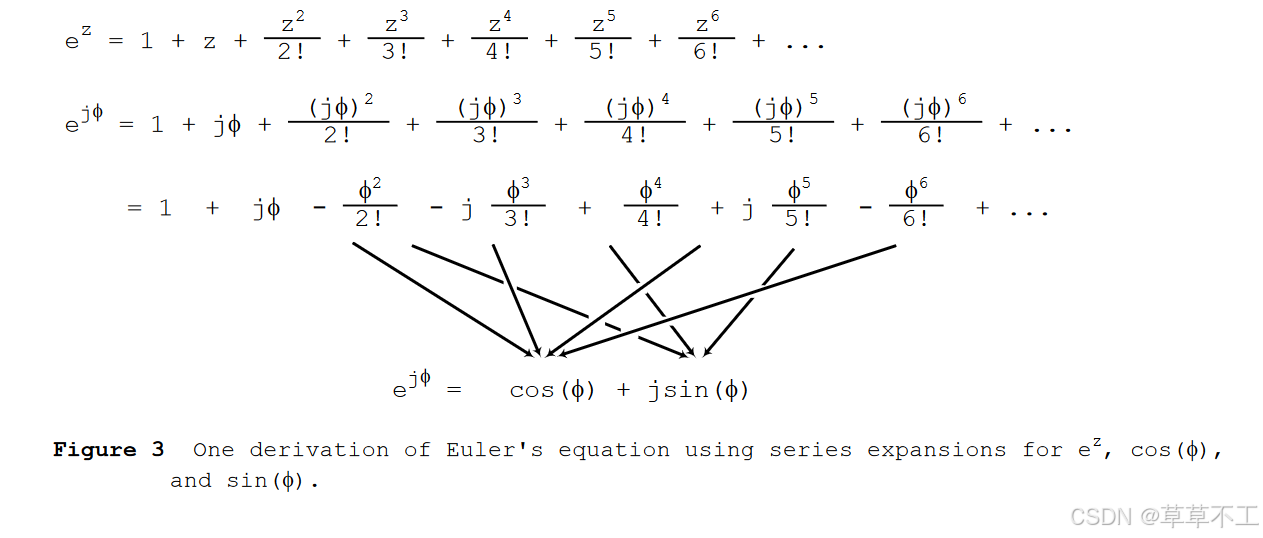
图 3 验证了 Eq.(7). 以及我们使用 Eq.(3). 极性形式对复数的表示:
M
e
j
ϕ
Me^{j\phi}
Mejϕ 。如果将图 3 第一行中的 z 替换为
−
j
ϕ
-j\phi
−jϕ,欧拉恒等式的形式会略有不同,但非常有用:
e
−
j
ϕ
=
c
o
s
(
ϕ
)
−
j
s
i
n
(
ϕ
)
(8)
e^{-j\phi} = cos(\phi) - jsin(\phi)\tag{8}
e−jϕ=cos(ϕ)−jsin(ϕ)(8)
Eq.(7). 和 Eq.(8). 的极值形式使我们受益匪浅,因为:
- 它简化了数学推导和分析——
- 将三角方程转化为简单的指数代数;
- 复数的数学运算遵循与实数完全相同的规则;
- 它使信号的相加仅仅是复数的相加(向量相加);
- 它是最简洁的符号;
- 它表明了数字通信系统是如何实现的,并用数学语言进行了描述;
我们将利用 Eq.(7). 和 Eq.(8). 来了解数字通信应用中使用正交信号的原因和方式。但首先,让我们深吸一口气,进入 "j "算子的 “奇幻地带”。你以前见过 j = − 1 j = \sqrt{-1} j=−1 的定义。换句话说,我们说 j 代表一个数字,当它与自己相乘时,结果是 -1。这个定义给初学者带来了困难,因为我们都知道,任何数字与自己相乘的结果总是正数。
遗憾的是,DSP 教科书往往先定义了符号 j,然后就有理由匆匆忙忙地介绍 j 运算符用于分析正弦信号的各种方法。读者很快就会忘记这个问题: j = − 1 j = \sqrt{-1} j=−1 究竟是什么意思?
其实, − 1 \sqrt{-1} −1 出现在数学舞台上已经有一段时间了,但直到 16 世纪必须用它来解三次方程时,才被认真对待。[1],[2] 数学家们开始勉强接受 − 1 \sqrt{-1} −1 这一抽象概念,而无需将其形象化,因为它的数学性质与正常实数的算术是一致的。
正是欧拉将复数等同于实数正弦和余弦,以及高斯出色地引入复数平面,才最终使 − 1 \sqrt{-1} −1 的概念在十八世纪的欧洲数学家心目中合法化。欧拉超越了实数的范畴,证明了复数与众所周知的实数三角函数正弦和余弦有着一脉相承的关系。正如爱因斯坦证明了质量和能量的等价性一样,欧拉也证明了实数正弦和余弦与复数的等价性。就像现代物理学家不知道电子是什么,但却了解它的特性一样,我们也不用担心 j 是什么,只要了解它的行为就可以了。对于我们来说,j 操作符意味着将复数逆时针旋转 90°,我们来看看为什么。
如图 4 所示,我们将通过研究 j = − 1 j = -1 j=−1 算子的数学性质来熟悉虚数的复平面表示法。

实轴上的任何数字乘以 j 都会得到一个位于虚轴上的虚积。图 4 中的例子表明,如果 +8 由位于正实数轴上的点表示,那么 +8 乘以 j 就会得到一个虚数 +j8,它的位置被逆时针旋转了 90°(从 +8 开始),使其位于正虚轴上。同样,将 +j8 乘以 j,又旋转了 90°,结果 8 位于负实数轴上,因为 j 2 = − 1 j^{2} =-1 j2=−1。将 -8 乘以 j,再旋转 90°,得到位于负虚轴上的-j8。任何用点表示的数字乘以 j,结果都是逆时针旋转 90°(相反,乘以 -j,结果是在复数平面上顺时针旋转 90°)。
如果在 Eq.(7). 中,代入
ϕ
=
π
2
\phi=\frac{\pi}{2}
ϕ=2π,我们可以得到:
e
−
j
π
2
=
c
o
s
(
π
2
)
+
j
s
i
n
(
π
2
)
=
0
+
j
1
=
j
(9)
e^{-j\frac{\pi}{2}} = cos(\frac{\pi}{2}) + jsin(\frac{\pi}{2})=0+j1=j\tag{9}
e−j2π=cos(2π)+jsin(2π)=0+j1=j(9)
这里要记住一点。如果您有一个复数,并由复数平面上的一个点表示,那么将该复数乘以 j 或 e − j π 2 e^{-j\frac{\pi}{2}} e−j2π 将得到一个在复数平面上逆时针旋转 90° 的新复数。不要忘记这一点,因为当你开始阅读正交处理系统的文章时,它将非常有用!
让我们暂停一下,喘口气。如果虚数和复数平面看起来有点神秘,不用担心,每个人一开始都会这样,但用得越多,就越会习惯。(毕竟 j 运算符曾让欧洲的数学家们困惑了几百年)。坦率的说,复数的数学含义不仅令人困惑,其术语也很怪异。用虚数这个词很不吉利,而用复数这个词简直太奇怪了。初见复数,我们会联想到 “复杂的数”,这是令人遗憾的,因为复数的概念其实并不复杂。我们只需知道,上述数学繁琐的过程是为了验证Eq.(2).(3)(7)(8)。现在,我们终于可以来谈谈时域信号了。
用复指数表示实数信号
好了,现在我们把注意力转移到时间函数的复数上。考虑一个幅度为 1 的数字,它的相位角随时间而增大。这个复数就是图 5(a) 所示的 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t 点。(这里的 2 π f 0 2\pi f_{0} 2πf0 项是以弧度/秒为单位的频率,它对应于 f 0 H z f_{0} Hz f0Hz 的频率)。随着时间 t 变大,复数的相位角增大,复数以逆时针方向绕复数平面的原点运行。图 5(a) 的实心点代表了这个复数,它被定格在某个时刻,如果频率 f 0 = 2 H z f_{0} = 2 Hz f0=2Hz,那么这个点每秒将绕圆旋转两圈。我们还可以看到另一个复数 e − j 2 π f 0 t e^{-j2\pi f_{0}t} e−j2πf0t (空心点)以顺时针方向运行,因为随着时间的增加,它的相位角会越来越负。

现在,让我们把两个 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t 和 e − j 2 π f 0 t e^{-j2\pi f_{0}t} e−j2πf0t 复表达式称为正交信号。它们各有正交的实部和虚部 (实部虚部正交称为正交信号) ,都是时间函数。这些 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t 和 e − j 2 π f 0 t e^{-j2\pi f_{0}t} e−j2πf0t 表达式在文献中通常被称为复指数。
我们也可以将这两个正交信号 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t 和 e − j 2 π f 0 t e^{-j2\pi f_{0}t} e−j2πf0t 视为图 5(b) 所示的两个相位旋转方向相反的向量。我们现在要坚持使用这种相位符号,因为它能让我们实现在复平面内表示实正弦的目标。Don’t touch that dial !
为了确保我们理解这些向量的行为,图 6(a) 显示了 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t 向量随着时间变动的三维路径。我们在页面中添加了时间轴,以显示向量的螺旋路径。图 6(b) 显示的是 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t 向量的连续路基。这个 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t 复数,或者说向量,以时间轴为中心,走着像开瓶器一样的螺旋路径。图 6(b) 中还显示了 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t 的实部和虚部的正弦和余弦投影。
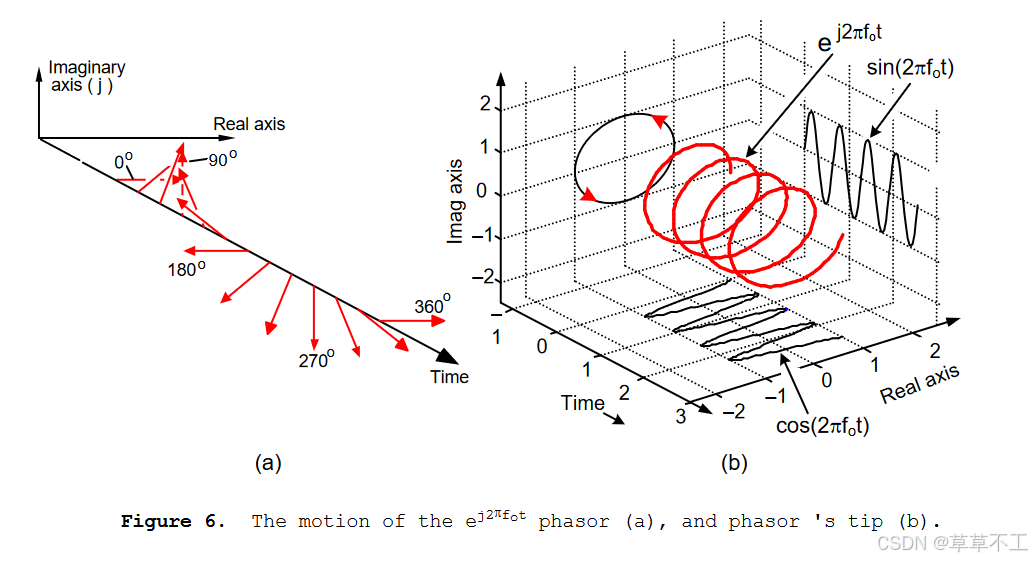
返回图 5(b) 并问自己:“当这两个相量沿相反方向旋转时,它们的矢量和是多少?”想一想…没错,相量的实部总是相加,而它们的虚部总是相消。这意味着这些 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t 和 e − j 2 π f 0 t e^{-j2\pi f_{0}t} e−j2πf0t 向量的总和将始终是纯实数。现代数字通信系统的实现就是基于这个属性!
为了强调这两个复杂正弦曲线的实数和的重要性,我们将绘制另一张图。考虑图 7 中的三维波形,该波形由两个一般幅度的复向量 e j 2 π f 0 t / 2 e^{j2\pi f_{0}t}/2 ej2πf0t/2 和 e − j 2 π f 0 t / 2 e^{-j2\pi f_{0}t}/2 e−j2πf0t/2 之和生成,围绕时间轴以相反方向旋转并沿时间轴移动。

考虑这些向量,现在很清楚为什么余弦波可以等于两个复指数之和:
c
o
s
(
2
π
f
0
t
)
=
e
j
2
π
f
0
t
+
e
−
j
2
π
f
0
t
2
=
e
j
2
π
f
0
t
2
+
e
−
j
2
π
f
0
t
2
(10)
cos(2\pi f_{0}t) = \frac{e^{j2\pi f_{0}t}+e^{-j2\pi f_{0}t}}{2} = \frac{e^{j2\pi f_{0}t}}{2}+\frac{e^{-j2\pi f_{0}t}}{2}\tag{10}
cos(2πf0t)=2ej2πf0t+e−j2πf0t=2ej2πf0t+2e−j2πf0t(10)
Eq.(10). 是一个众所周知的表达式,也被称为欧拉恒等式之一。我们可以通过求解 Eq.(7) (8) ,将
j
s
i
n
(
ϕ
)
jsin(\phi)
jsin(ϕ) 消去,得出这个恒等式。我们可以用同样的方法求得
j
c
o
s
(
ϕ
)
jcos(\phi)
jcos(ϕ),并证明正弦波也是两个复指数的和:
s
i
n
(
2
π
f
0
t
)
=
e
j
2
π
f
0
t
−
e
−
j
2
π
f
0
t
2
j
=
j
e
−
j
2
π
f
0
t
2
−
j
e
j
2
π
f
0
t
2
(11)
sin(2\pi f_{0}t) = \frac{e^{j2\pi f_{0}t}-e^{-j2\pi f_{0}t}}{2j} = \frac{je^{-j2\pi f_{0}t}}{2}-\frac{je^{j2\pi f_{0}t}}{2}\tag{11}
sin(2πf0t)=2jej2πf0t−e−j2πf0t=2je−j2πf0t−2jej2πf0t(11)
仔细看看Eq.(10) (11). 。它们是余弦波和正弦波使用复数符号的标准表达式。为了防止读者像那些复杂的向量一样晕头转向,我们要明白从图 5 到图 7 的唯一目的是验证 Eq.(10) (11) 中给出的余弦和正弦波的复数达式。 这两个式子,加上此前的 Eq.(7) (8). 是正交信号处理的罗塞塔石碑。

我们现在可以轻松地在实正弦函数和复指数之间来回转换。强调一下,我们正在学习如何把那些可以通过同轴电缆传输或数字化并存储在计算机内存中的实信号用复数来表示。的确,复数的各个组成部分都是实数,但我们以特殊的方式处理这些部分——我们以正交方式处理它们。
文章的上半段就先翻译到这里,下半段会从频域的角度出发,并辅以许多频率域的图形,作为这个系列的「中」篇。本文虽然一直在说正交,但缺少了对两个实信号的正交性本身的讨论,只是讲了 e j 2 π f 0 t e^{j2\pi f_{0}t} ej2πf0t的实部虚部是正交的,我们会在这个系列的「下」篇中讲讲正交性本身的定义。翻译错误之处欢迎指正!

























 2309
2309

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








