线性代数
行列式
行列式概念的引进
对角线法则:
- 二阶的快捷方法(ad-bc)
- 三阶的快捷方法
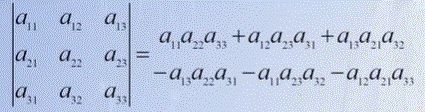
n阶行列式
D=ai1Ai1+ai2Ai2+……+ainAin
D=a1jA1j+a2jA2j+……+anjAnj
特殊行列式的计算
对角行列式/下三角行列式/上三角行列式=对角线元素的乘积
行列式的性质
- 行列式=转置的行列式
- 互换两行,行列式变号。
- 若行列式中有两行元素完全相同,则行列式为0.
- aj1Ai1+aj2Ai2+……+ajnAin=D(i=j)
aj1Ai1+aj2Ai2+……+ajnAin=0(i≠j) - 用数k乘行列式某一行中所有元素,等于用k乘此行列式
- 行列式某一行元素加上另一行对应元素的k倍,行列式的值不变。
- 若某行列式某一行元素是两数之和,则行列式可拆成两个行列式之和。
- 若某行列式某一行元素是m个元素之和,则行列式可写成m个行列式之和。
行列式的计算
简便求解:化0,降阶,求解。
克莱姆法则
克莱姆法则表达:若系数行列式不等于零,则方程组有解且解唯一,解的表达式为D(j)/D
- 定理1: x ( j ) = D ( j ) D x(j)=\frac{D(j)}{D} x(j)=DD(j)
- 定理2:若方程组的系数行列式不为零,则方程组有唯一解。
- 若齐次方程组的系数行列式不为零,则方程组有唯一零解。
范德蒙行列式
条件:元素按升幂排列,幂指数成等差数列
D=π(a(i)-a(j))=(a2-a1)(a3-a1)……(an-a1)(a3-a2)(a4-a2)……(an-a2)……*(an-an-1)
逆序数与行列式
奇排列:逆序数=奇数
偶排列:逆序数=偶数
对换:在一个排列中,任意对调两个元素,其余元素不变,即得到一个新排列,这样一种变换成为对换。
对换性质:
- 任意一个排列经一次对换后改变奇偶性。
- 在n个元素的全排列中,奇偶排列各站一半,为n!/2
结论:


这个例子妙啊:

行列式展开定理
D=ai1Ai1+ai2Ai2+……+ainAin
D=a1jA1j+a2jA2j+……+anjAnj
矩阵
矩阵是什么
懂的都懂 →_→
单:matrix 复:matrices(奇怪的知识增加了!))
几种特殊的矩阵
- 方阵 square matrix
- 零矩阵
- 对角矩阵(必是方阵)
- 单位矩阵:元素全为1的对角阵
- 数量阵:元素全为K的对角阵
- 三角阵(非零元素在右上或非零元素在左下)
- 梯形阵(0元素在右上或0元素在左下)
矩阵的运算
线性运算
- 负矩阵:每个元素取相反数
- 数乘:A中的每个元素*K
- AB≠BA
- 存在AB=AC,但B≠C
- 矩阵乘法中有非零的零因子
转置
(
A
T
)
T
=
A
(A^T)^T=A
(AT)T=A
(
A
+
B
)
T
=
A
T
+
B
T
(A+B)^T=A^T+B^T
(A+B)T=AT+BT
(
k
A
)
T
=
k
A
T
(kA)^T=kA^T
(kA)T=kAT
(
A
B
)
T
=
B
T
A
T
(AB)^T=B^TA^T
(AB)T=BTAT
- 对称阵
若一个矩阵,它的转置和它本身相等,则该矩阵叫做对称阵。 - 反对称阵
A T = − A A^T=-A AT=−A
方阵的行列式
- 非奇异方阵:方阵的行列式不为0.
- 奇异方阵:方阵的行列式为0.
- ∣ k A ∣ = k n ∗ ∣ A ∣ |kA|=k^{n}*|A| ∣kA∣=kn∗∣A∣
- |AB|=|A||B|
伴随矩阵

- AA*=A*A=|A|E
矩阵的初等变换
(1)对换矩阵中第i,j两行(列)的位置
(2)用非零常数k乘第i行(列)
(3)将矩阵的第j行(列)乘常数k后加到第i行(列)对应元素上
矩阵的秩
- 秩的定义:矩阵A的所有不等于0的子式的最高阶数成为矩阵A的秩。
- 若两个矩阵有相同的秩,则这两个矩阵有相同的标准型。
- 若两个矩阵等价,则他们的秩相同。
- 满秩矩阵:若方阵A的秩与其阶数相等,则称A为满秩矩阵,否则称为降秩矩阵。
- 设A为满秩矩阵,则A的标准形为同阶单位阵E,即A等价于E。
- 若方阵A的行列式|A|≠0,则称A为非奇异矩阵;若|A|=0,则称A为奇异矩阵。
- 满秩矩阵-----非奇异矩阵,降秩矩阵----奇异矩阵
初等矩阵
- 初等矩阵:对单位阵进行一次初等变换后得到的矩阵称为初等矩阵。
- 行变换相当于左乘初等矩阵,列变换相当于右乘初等矩阵
- 等价:
A满秩-----A等价于E----A非奇异----A=P1P2……Pm;(P为初等矩阵) - 推论:矩阵A与矩阵B等价的充要条件是存在m阶及n阶满秩矩阵P、Q,使B=PAQ
- 推论:若P、Q为满秩矩阵,则r(A)=r(PA)=r(PAQ)=r(AQ)
例题
逆矩阵的定义与可逆条件
-
逆矩阵:对n阶方阵A,若有n阶矩阵B使得AB=BA=E,则称B为A的逆矩阵,称A为可逆的。
-
逆阵唯一。
-
定理:n阶方阵A可逆的充要条件:|A|≠0.
-
公式: A ( − 1 ) = 1 ∣ A ∣ A ∗ A^{(-1)} =\frac{1}{|A|}A^* A(−1)=∣A∣1A∗
-
因为 ∣ A A − 1 ∣ = ∣ A ∣ ∣ A − 1 ∣ = ∣ E ∣ = 1 |AA^{-1}|=|A||A^{-1}|=|E|=1 ∣AA−1∣=∣A∣∣A−1∣=∣E∣=1
所以 ∣ A − 1 ∣ = ∣ A ∣ − 1 |A^{-1}|=|A|^{-1} ∣A−1∣=∣A∣−1 -
A 可逆=A非奇异=A满秩
-
逆矩阵的性质
(1)A可逆,则 ∣ A − 1 = 1 ∣ A ∣ |A^{-1}=\frac{1}{|A|} ∣A−1=∣A∣1
(2)A可逆,则 A − 1 A^{-1} A−1可逆, ( A − 1 ) − 1 = A (A^{-1})^{-1}=A (A−1)−1=A
(3)AB=E,则 B = A − 1 B=A^{-1} B=A−1
(4) ( A T ) − 1 = ( A − 1 ) T (A^T)^{-1}=(A^{-1})^T (AT)−1=(A−1)T
(5) ( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
(6) ( k A ) − 1 = 1 k A − 1 ( k ≠ 0 ) (kA)^{-1}=\frac{1}{k}A^{-1} (k\ne0) (kA)−1=k1A−1(k=0) -
初等矩阵的性质:
E − 1 ( i , j ) = E ( i , j ) E^{-1}(i,j)=E(i,j) E−1(i,j)=E(i,j)
e − 1 ( i ( k ) ) = E ( i ( 1 k ) ) e^{-1}(i(k))=E(i(\frac{1}{k})) e−1(i(k))=E(i(k1))
E − 1 ( i , j ( k ) ) = E ( i , j ( − k ) ) E^{-1}(i,j(k))=E(i,j(-k)) E−1(i,j(k))=E(i,j(−k))
(即初等矩阵的逆矩阵仍为同类型的初等矩阵) -
逆阵的求法2----初等变换法

-
逆矩阵的求法3----定义法
猜一个矩阵B,验证AB=E,则B是A的逆矩阵 -
逆矩阵的求法4----用定义证明已给的矩阵是逆矩阵
分块矩阵
- 定义:将矩阵用若干纵横直线分成若干个小块,每一小块成为矩阵的子块(或字阵),以子块为元素形成的矩阵称为分块矩阵。
- 分块矩阵的运算
线性运算——加法和数乘
乘法运算——符合乘法要求
转置运算——大块小块一起转 - 特殊的分块矩阵
准对角阵:
A可逆—— ∀ \forall ∀Ai可逆

|A|=|A1||A2|……|As|
r(A)=r(A1)+r(A2)+……+r(As)
其他运算:


分块三角阵

分块斜对角阵


求解矩阵方程
- AX=B

- XA=B

- AXB=C
向量
n维向量及其线性运算
- 线性组合:设向量b,a1,a2,…,am,若存在一组数k1,k2,…,km使b=k1a1+k2a2+…+kmam则称向量b可由向量a1,a2,…,am线性表示,或称b是a的线性组合。
- 向量组的等价:若向量组I中每个向量都可由向量组II线性表示,则称向量组I可由向量组II线性表示;若I与II可互相线性表示,则称向量组I与II等价。
向量组的线性相关性
- 线性相关性:设向量组a,若存在一组不全为0的数k,使k1a1+k2a2+…+kmam=0,则称向量组a线性无关。
- 注意:
(1)若向量组只有一个向量时:若为零向量,则它线性相关,否则线性无关。
(2)两个向量线性相关的充要条件是对应分量成比例。
(3)任一含有零向量的向量组线性相关。
相关性的判定定理
- 定理1:向量组a线性相关的充要条件是其中至少有一个向量可由其余m-1个向量线性表示。
- 定理2:设向量组a1,a2,…,am线性无关,而向量组β线性相关,则β可由a线性表示且表示式唯一。
- 定理3:在一个向量组中,若有一个部分向量组线性相关,则整个向量组也必定线性相关。反之不对。
- 定理4:m个n维向量线性相关的充要条件是这m*n的矩阵的秩<m
- 推论:当m>n,m个n维向量线性相关
- 任意m个n维向量线性无关的充要条件是由它们构成的矩阵的秩=m
- 任意n个n维向量线性无关的充要条件是由它们构成的方针的行列式不等于零,或r(A)=n;
- 定理5:线性无关的向量组,添加分量后仍旧线性无关。
向量组的极大无关组与秩的定义
-
极大无关组:设向量T的部分向量组满足:
i)组内线性无关
ii)T中任一向量可由该部分向量组表示
iii)T中任一向量加入该部分向量组后变得线性相关。 -
注意:
i)线性无关向量组的极大无关组就是其本身。
ii)向量组与其极大无关组等价
iii)同一个向量组的极大无关组不唯一,但它们是等价的。 -
极大无关组的性质:
-
定理1:设有两个n维向量,a(r )和b(s),若向量组a线性无关,且可由向量组b线性表示,则r≤s.
-
推论:若向量组a( r)可由向量组b(s)线性表示,且r>s,则向量组a(r )线性相关。
-
推论2:任意两个线性无关的等价向量组所含向量的个数相等。
-
向量组的秩:向量组A的极大无关组所含向量的个数,称为向量组的秩。
-
推论:
**等价的向量组有相同的秩。
有相同秩的向量组不一定等价。
矩阵等价则矩阵的秩相同。
矩阵的秩相同则矩阵等价。
**
向量组的极大无关组与秩的求法
- 矩阵的行秩与列秩相等,为矩阵的秩。
- 向量组的秩与该向量组所构成的矩阵的秩相等。
- 极大无关组的求法:
列摆行变换法

例:
- 推论:r(A*B)≤min{r(A),r(B)}
向量空间
- 运算的封闭性:设V是n维向量的非空集合,称V对于向量加法及数乘两种运算封闭。
- 设V是n维向量的非空集合,如果V对于向量加法及数乘两种运算封闭,则称集合V为n维向量空间,简称为向量空间。
- 子空间:设W,V是向量空间,若W ⊂ \subset ⊂V,则称W是V的子空间。
- 向量空间的基:若n维向量空间V中的向量组a1,a2,…,ar满足线性无关且V中的向量均可由a1,a2,…,ar线性表示,则称a1,a2,…,ar是V的一个基。
- 基中所含向量个数r成为向量空间的维数。
- 设a1,a2,…,ar是向量空间V的基,b ∈ \in ∈V且b=k1a1+k2a2+…+kr*ar,则称系数k1,k2,…,kr为b在基a1,a2,…,ar下的坐标。
向量组的正交性
- 向量的内积:设有向量a=(a1,a2,…,an),b=(b1,b2,…,bn),则a1b1+a2b2+…+an*bn称为向量a与b的内积,记为(a,b)。
- (a,b)=(a, b T b^T bT)
- (a,b)=(b,a)
- (ka,b)=k(a,b)=(a,kb)
- (a+b,c)=(a,c)+(b,c)
- (a,a)= ∣ a ∣ 2 |a|^2 ∣a∣2
- 向量的正交性:若(a,b)=0,则称这两个向量正交。
- 若m个n维非零向量两两正交,则称向量组为正交向量组,简称正交组。
- 定理:正交向量组中的向量都线性无关。
- 向量组的正交规范化

- 正交矩阵:若n阶方阵A满足 A T A^T AT*A=E,则称A为n阶正交矩阵。
- 若A为n阶正交矩阵,则|A|=±1
- 若A为n阶正交矩阵,则 A T A^T AT与 A − 1 A^{-1} A−1也是正交矩阵。
- 定理:矩阵A为正交矩阵
≡
\equiv
≡A的行(列)向量组为单位正交向量组
证明:




























 1614
1614

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








