数理知识-求导篇-基础求导知识

数理知识-求导篇-基础求导知识

---

前言

机器学习及深度学习领域的数理推导总会用到很多求导的理论知识，出现的频率非常高。因此汇总一些求导的知识非常重要。

一、导数的定义

导数（Derivative），也叫导函数值。又名微商，是微积分中的重要基础概念。当函数y=f（x）的自变量x在一点x0上产生一个增量Δx时，函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在，a即为在x0处的导数，记作f’（x0）或df（x0）/dx。

导数是函数的局部性质。一个函数在某一点的导数描述了这个函数在这一点附近的变化率。如果函数的自变量和取值都是实数的话，函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。导数的本质是通过极限的概念对函数进行局部的线性逼近。例如在运动学中，物体的位移对于时间的导数就是物体的瞬时速度。

不是所有的函数都有导数，一个函数也不一定在所有的点上都有导数。若某函数在某一点导数存在，则称其在这一点可导，否则称为不可导。然而，可导的函数一定连续；不连续的函数一定不可导。

对于可导的函数f(x)，x↦f’(x)也是一个函数，称作f(x)的导函数（简称导数）。寻找已知的函数在某点的导数或其导函数的过程称为求导。实质上，求导就是一个求极限的过程，导数的四则运算法则也来源于极限的四则运算法则。反之，已知导函数也可以反过来求原来的函数，即不定积分。

微积分基本定理说明了求原函数与积分是等价的。求导和积分是一对互逆的操作，它们都是微积分学中最为基础的概念。[1]

二、基本初等函数的导数

三、复杂导数的运算

1、导数的四则运算：

2、原函数与反函数导数关系（由三角函数导数推反三角函数的）：

y=f（x）的反函数是x=g（y），则有y’=1/x’。

3、复合函数的导数的求导方法：

复合函数对自变量的导数，等于已知函数对中间变量的导数，乘以中间变量对自变量的导数（称为链式法则）。

4、变限积分的求导法则：

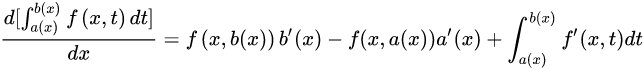
（a（x）,b（x）为子函数）

四、矩阵求导的拓展

数理知识-矩阵篇-矩阵/向量求导

可参考

[1]百度百科：导数的基本概念