矢量场的旋度----环量和旋度

1、环量

如果矢量场是：

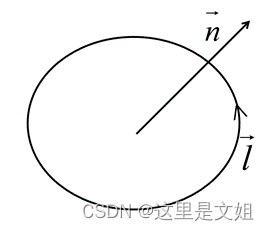
取有向的闭合曲线 ，闭合曲线所限定的曲面的正法线方向符合右手螺旋定则。

环量定义：

空间中可以有无穷多个曲面共同构成，也可以由无穷多个有限曲线一个叠加一个构成。所以我们只需要研究任意一个环路上面的情况就足以反应这个场。但是这只是一种整体的概念，我们就同一个环路来说，他的大小几何形状不变，但是我们要注意他的空间的方位不一样，所以对A的积分值也是不一样的。

举例：如果我们的河流里面有我们的流速场，不妨说在这个地方有个漩涡就是我们的流线。如果沿着这个流线对速度进行积分的话，环量不等于0。那么如果环量不等于0，我们就可以推断这个地方肯定有漩涡。如果我们的积分环路和这个流速方向垂直的话，环量等于0。

因此我们可以看到环量具有工程概念，如果我们在某一点的领域，沿某一个环路对矢量进行积分，结果不等于0，我们可以初步判定这个地方有没有漩涡。但是漩涡会围着一个轴转，我们想知道轴在哪里？当我们积分的路径和这个轴所垂直的平面在一个平面的时候，积分最大。所以轴和积分路径的发现方向垂直时，环量最大。因此我们关心的问题是，同样一个环路，不同的方向n什么时候环量最大。这样就引入了我们所谓的旋度。

2、旋度

，某一点单位面积内的环量，即环量密度

在直角坐标系中可以写出：

n方向的单位矢量：

我们取一个矢量：

那么环量密度等于： ，n方向的环量密度就是这个v矢量在这个方向的投影。如果n和v的方向一致得到最大的环量密度。v的方向就是环量密度最大的方向。就是漩涡所在平面垂直的轴的方向。我们把这个矢量就称作他在这一点的旋度。

旋度定义公式：

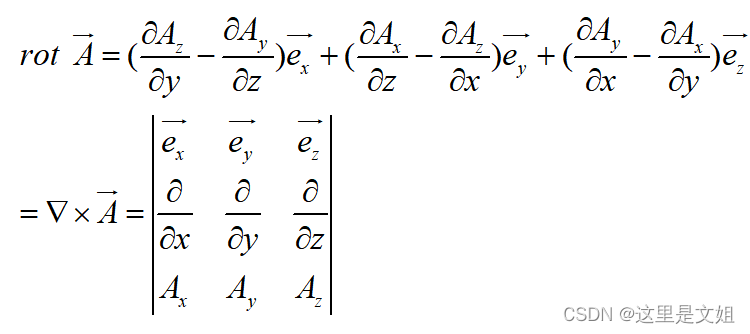
前言知识

场的概念---数量场（标量场）和矢量场介绍理解-CSDN博客

数量场（标量场）的方向导数及梯度推导、哈密顿算符定义-CSDN博客

矢量场的散度----通量和散度概念讲解-CSDN博客