活动地址:CSDN21天学习挑战赛
1 简介
牛顿法也叫牛顿迭代法,它是一种求根算法,也可以求函数的极小值。它的基本思想是在现有极小点估计值附近对f(x)做二阶泰勒展开,找到下一个极小点,继续迭代的过程。
2 牛顿法原理
输入:目标函数f(x),函数梯度为,计算精度
输出:f(x)的零点
(1)选出初始值,k=0;
(2)计算和梯度
;
(3)带入迭代公式进行参数更新:
推导该迭代公式
设第k次迭代点为
,过该点做曲线的切线,斜率则为
,进而可得到切线方程为:
接着求该曲线与x轴的交点坐标:
则交点的横坐标为新的迭代点的横坐标,整理得:
确定迭代次数或者精度;
(4)如果,停止迭代,令
=
,输出结果;否则继续迭代。
实验部分:雷神之锤代码计算
#include<iostream>
using namespace std;
//计算 1/((x)^(1/2))
float Q_rsqrt( float number ) {
long i;
float x2, y;
const float threeHalfs = 1.5f;
x2 = number * 0.5f;
y = number;
i = * ( long * ) &y; // evil floating point bit level hacking
i = 0x5f3759df - ( i >> 1 ); // What the fuck?
y = * ( float * ) &i;
y = y * ( threeHalfs - ( x2 * y * y ) ); // 1st iteration
// y = y * ( threeHalfs - ( x2 * y * y ) ); // 2nd iteration, this can be removed
return y;
}
int main() {
float x1=4;
float x2=2;
float x3=25;
printf("%f",Q_rsqrt(x3));
return 0;
}2.1 Hessen矩阵
Hessen矩阵存储了二阶可导的多元函数的二阶导数,Hessen矩阵可用于多元函数的泰勒展开,一般用H表示 Hessen矩阵。

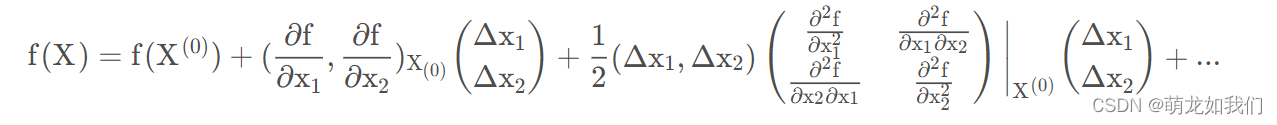
上式可简写为:
其中
为求导后在第k个迭代点的梯度向量;
表示第k次迭代时的Hessen矩阵
当f(x)去到最值时,f'(x)=0,令此时的x=k+1(其中意思相同)
整理后得到x的迭代公式:
2.2 拟牛顿法条件
对(2)式子操作:
记,
,则:
记代入上式得:
即 该式为拟牛顿法条件。
从这里可以看出此时牛顿法需要 计算矩阵的逆,计算会很麻烦,甚至不存在逆矩阵,这样就需要拟牛顿法了。
3 拟牛顿法
拟牛顿法的思想是找到矩阵的逆的替代者,主要有DFP和DFGS方法。
参考
(43条消息) 泰勒展开与黑塞矩阵(Hessian Matrix)_老实人小李的博客-CSDN博客_泰勒展开式的矩阵形式






















 400
400











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








