高斯消元法

线性方程组的求解

其实高斯消元我们在学习线性代数求解线性方程组的时候学习过，首先简单复习一下矩阵初等变换

矩阵初等变换：

(1) 交换矩阵的两行或两列（对调$i,j$两行记为$r_i<->r_j$）

(2) 以一个非零数$k$乘矩阵的某一行（列）所有元素（第$i$行乘以$k$记为 $r_i\ast k$ ）

(3) 把矩阵的某一行（列）所有元素乘以一个数$k$后加到另一行（列）对应的元素(第j行乘以k加到第i行记为 $r_i+k\ast r_j$)

对于下列$n$元一次线性方程组:

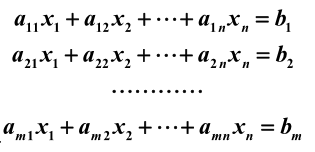
我们用$系数矩阵\ast 未知数矩阵=常数矩阵$来表示上述线性方程组:

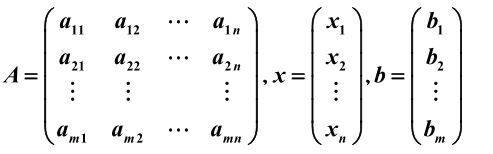
然后我们称矩阵$(A,b)$为该方程组的增广矩阵:

消元法解线性方程组过程实际上是对方程组未知数的系数和常数项作有限制的运算，未知变量并未参与运算。因此，将解线性方程组的消元运算移植到矩阵变换中就是对线性方程组的增广矩阵进行三种初等变换并化简为行阶梯矩阵或者行最简形矩阵

在线性代数的学习中，我们是通过矩阵的秩来判断线性方程组是否有解，但是如果写成程序，就需要分以下几种情况讨论解：

① 无解
当方程中出现$(0,0,\dots ,0,a)$的形式，且$a!=0$时；或者某一列全为$0$；说明是无解的

② 唯一解
如果行阶梯矩阵形成了严格的上（下）三角阵，或者可以化为$n$阶行最简矩阵，那么就有唯一解

③ 无穷解
存在无穷解即代表至少有一行元素全为$0$（包括第$n+1$行），那么如果有$k$行就代表有$k$个自由变元

高斯消元法

高斯消元法就是利用矩阵初等变换，将增广矩阵变换为行阶梯矩阵，进而通过逐层回带求出解。总的来说主要进行以下步骤（以下三角行阶梯矩阵为例）：

• 消元第一步：每次考虑$a[i][i]$，然后从第$i$列第$i$行以下中找出该列最大的元素，并将那一行和该行互换位置。之所以找最大的，是因为下面要用该数做除法，而除数越小误差越大（不太懂记住算了）

• 消元第二步：如果上面找到的最大值仍为$0$证明无解，直接返回

• 消元第三步：第$i$列从第$j=i+1$行开始，先除以$a[i][i]$并保存结果，接着该行都减去该行乘以上述结果，以达到将第$j$行第$i$列消为$0$的目的。重复上述三步$n$次即可

• 消元第四步：由于我们上述化的是下三角型行阶梯矩阵，那么最后一行只有一个变量，倒数第二行有两个变量…以此类推，那么之间回带求出结果保存在$a[i][n+1]$位置上

const double esp = 1e-8;
double a[1005][1005];
int n;

bool gauss() {
    for (int i = 1; i < n; i++) {
        int temp = i;
        for (int j = i + 1; j <= n; j++)
            if (fabs(a[j][i]) > fabs(a[temp][i])) temp = j;
        //如果当前列的最大值仍然为0，无解
        if (fabs(a[temp][i]) < esp) return false;
        //与最大主元所在行交换
        if (temp != i) {
            for (int j = i; j <= n + 1; j++)
                swap(a[i][j], a[temp][j]);
        }
        double p;
        for (int j = i + 1; j <= n; j++) {//消元
            p = a[j][i] / a[i][i];
            for (int k = i; k <= n + 1; k++)
                a[j][k] -= a[i][k] * p;
        }
    }
    //回代求解
    for (int i = n; i >= 1; i--) {
        for (int j = i + 1; j <= n; j++)
            a[i][n + 1] -= a[i][j] * a[j][n + 1];
        a[i][n + 1] /= a[i][i];
    }
    return true;
}

高斯消元判断解的情况

常规的高斯消元只适用于快速求出有解的情况，但是对于区分无穷解和无解以及在无穷解下有多少个自由变元比较难搞，因此需要对高斯消元作出适当改进：

一般的高斯消元都是考虑主对角线的每个位置$(i,i)$，如果有解那么行列的下标永远是相同的，但是如果出现了无穷解，即代表某行为$0,0,0,...,0$，此时我们应该将它暂时放置，行不变但是列继续下移，直到能在下面找到$a[r][c]!=0$，那么将全为$0$的这行交换到下面，重复这个操作，最后就能保证所有的自由变元的行都在矩阵的下方，例如：

$\left[\begin{array}{ccccc}1& 2& -3& 0& 1\\ 0& 0& 0& 0& 0\\ 0& 0& 1& 3& 4\\ 0& 0& 0& 1& 6\end{array}\right]⟹\left[\begin{array}{ccccc}1& 2& -3& 0& 1\\ 0& 0& 1& 3& 4\\ 0& 0& 0& 1& 6\\ 0& 0& 0& 0& 0\end{array}\right]$

显然若记录行的向量最后没有到达$n+1$代表出现了无穷解或者无解，若某行为$0,0,0,...,0,1$则代表无解；若某行为$0,0,0,...,0$则代表有无穷解，设此时列的下标为$i$，那么自由变元的个数就为$n-i+1$。

洛谷P2455

int n;
double a[105][105];

int guass() {
    int r = 1;
    for (int c = 1; c <= n; c++) {
        int temp = r;
        for (int i = r + 1; i <= n; i++) {
            if (fabs(a[i][c]) > fabs(a[temp][c])) temp = i;  //每行第一个非零元素越大误差越小
        }
        if (fabs(a[temp][c]) < eps) continue;  //这步是实现行列异步的关键
        for (int j = c; j <= n + 1; j++) swap(a[r][j], a[temp][j]);
        for (int j = n + 1; j >= c; j--) a[r][j] /= a[r][c];
        for (int i = r + 1; i <= n; i++) {
            for (int j = n + 1; j >= c; j--)
                if (fabs(a[i][c]) >= eps) {
                    a[i][j] -= a[i][c] * a[r][j];
                }
        }
        r++;
    }
    if (r <= n) {
        for (int i = 1; i <= n; i++) {
            bool ok = 0;
            for (int j = 1; j <= n; j++)
                if (fabs(a[i][j]) > eps) ok = 1;
            if (ok) continue;
            if (fabs(a[i][n + 1]) >= eps) return -1; //无解
            else return 0;   //无穷解
        }
    }
    //有唯一解，回代求解
    for (int i = n; i >= 1; i--) {
        for (int j = i + 1; j <= n; j++)
            a[i][n + 1] -= a[i][j] * a[j][n + 1];
        a[i][n + 1] /= a[i][i];
    }
    return 1;
}

高斯·约旦消元法

传送门