文章目录
- Structured Support Vector Machine
- Unified Framework(统一框架:两步走,三问题)
- Example Task: Object Detection(示例任务:目标检测)
- Outline(大纲)
- Separable case(可分情形)
- Non-separable case(不可分情形)
- Considering Errors(考虑误差)
- Regularization(正则化)
- Structured SVM(结构化支持向量机)
- Cutting Plane Algorithm for Structured SVM(切割平面算法)
- Multi-class and binary SVM(多类别与二元支持向量机)
- Beyond Structured SVM(open question)(下一步支持向量机(开放问题))
Structured Support Vector Machine
结构化学习要解决的问题,即需要找到一个强有力的函数 f
f
:
X
→
Y
f : X \rightarrow Y
f:X→Y
- 输入和输出都是具有结构化的对象;
- 对象可以为:sequence(序列),list(列表),tree(树结构),bounding box(包围框),等等
其中,X是一种对象的空间表示,Y是另一种对象的空间表示。
Unified Framework(统一框架:两步走,三问题)
two steps(两步)

第一步:训练
-
寻找一个函数 F
F : X × Y → R \mathrm{F} : X \times Y \rightarrow \mathrm{R} F:X×Y→R -
F(x, y): 用来评估对象x和y的兼容性 or 合理性
第二步:推理 or 测试
- 给定一个对象 x,求得:
y ~ = arg max y ∈ Y F ( x , y ) \tilde{y}=\arg \max _{y \in Y} F(x, y) y~=argy∈YmaxF(x,y)
即给定任意一个x,穷举所有的y,将(x, y)带入F,找出最适当的y作为系统的输出。
three problems(三问题)
-
Q1: Evaluation(评估)
- What: F(x, y) 的形式
-
Q2: Inference(推理)
- How: 如何解决 “arg max” 问题
y ~ = arg max y ∈ Y F ( x , y ) \tilde{y}=\arg \max _{y \in Y} F(x, y) y~=argy∈YmaxF(x,y)
即转换为最优化的求解问题。
- How: 如何解决 “arg max” 问题
-
Q3: Training(训练)
- 给定训练数据,如何求解 F(x, y)?
Example Task: Object Detection(示例任务:目标检测)
Evaluation
对 F ( x , y ) F(x,y) F(x,y)做一些假设,可以让之后的任务变得容易一点,这里假设 F ( x , y ) F(x,y) F(x,y)是线性的。

x x x是一张图片, y y y是一个bounding box。也就是 F ( x , y ) F(x,y) F(x,y)可以写成一个weight( w w w),跟一个特征向量 ϕ ( ) ϕ() ϕ()的内积。 w w w是Q3里通过训练数据学习出来的,而 ϕ ( ) ϕ() ϕ()是人工定的。
开放问题: F ( x , y ) F(x,y) F(x,y)可以是非线性的吗?
你可能知道说 F ( x , y ) F(x,y) F(x,y)如果是线性的话,其实是很弱的,做不了什么太厉害的事情,必须要依赖一个复杂的抽特征的方式来得到一个好的结果。但这可能不是我们想要的,我们希望机器能做更复杂的事而不是有太多人的知识介入在里面。关于 F ( x , y ) F(x,y) F(x,y)非线性的研究还很少,因为 F ( x , y ) F(x,y) F(x,y)不是线性的话,等会要讨论的都不成立了。所以我们之后,多数情况都是假设 F ( x , y ) F(x,y) F(x,y)是线性的。
Inference
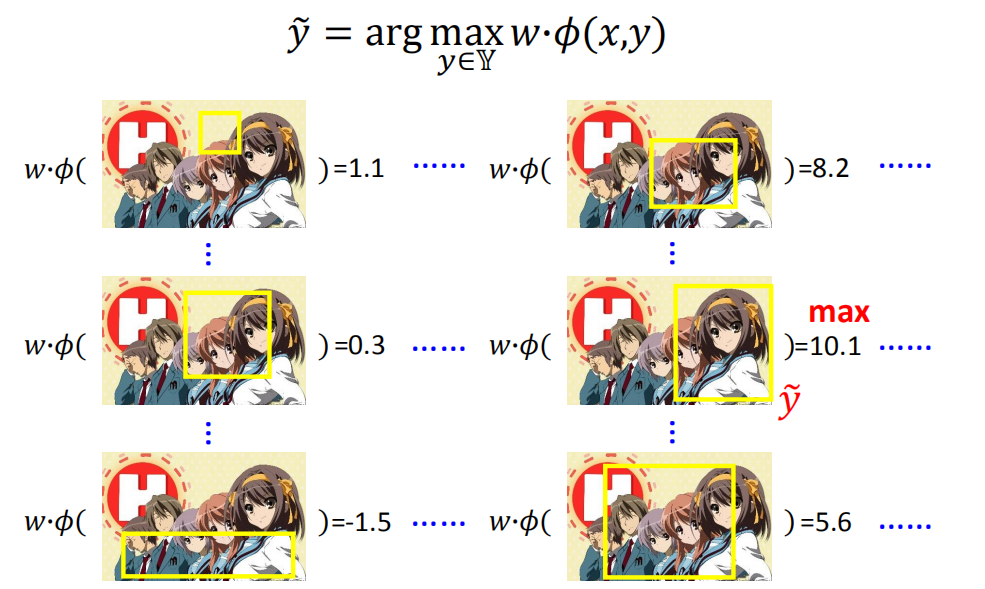
给你一个xx,你要去穷举所有可能的y,看哪一个y可以让你的评估函数( w ⋅ ϕ ( x , y ) w⋅ϕ(x,y) w⋅ϕ(x,y))最大,那么需要一个演算法有效的做这件事情。
y
~
=
arg
max
y
∈
Y
w
⋅
ϕ
(
x
,
y
)
\tilde{y}=\arg \max _{y \in \mathbb{Y}} w \cdot \phi(x, y)
y~=argy∈Ymaxw⋅ϕ(x,y)
以目标检测为例,就要穷举所有可能的bounding box,对每个bounding box都要算一个分数(
w
⋅
ϕ
(
)
w⋅ϕ()
w⋅ϕ())。比如上图右边中间的bounding box得到的分数最大,那就把这个bounding box作为结果
y
^
\hat{y}
y^。你可能觉得穷举听起来是一个很花时间的东西,事实上我们有比较有效率的方法去做穷举(需要自己去想)。

- 目标检测(取决于ϕ(x, y))
- Branch & Bound algorithm(分支定界法)
- Selective Search(选择性搜索)
- 序列标记(会在下一章着重复现,其取决于 ϕ ( x , y ) \phi(x,y) ϕ(x,y))
- Viterbi Algorithm(维特比译码算法)
- 遗传算法(基因演算)
使用什么算法取决于你的task,如果你有不同的task,就要想不同的算法。甚至同一个task,特征 ϕ ( x , y ) \phi(x,y) ϕ(x,y)定义不同,也需要不同的算法。
你可以想象这个统一框架是有用的,虽然没有教你问题具体怎么解决,给你一个结构化学习的问题,如果你不知道这个统一框架,那你就不知道从何解起,而统一框架给了你一个思路。
如果你不知道Q2怎么解,可以使用经典算法,可以解决很多的问题,不过有时候找到的不一定是准确的结果。
开放问题:如果我们没有办法找到一个准确的结果,也就是arg max只能有一个近似的结果,那么这对我们的结果影响有多大?
在以下课程里,我们都假设Q2已经解决了。
Training
训练数据:
{
(
x
1
,
y
^
1
)
,
(
x
2
,
y
^
2
)
…
,
(
x
N
,
y
^
N
)
}
\left\{\left(x^{1}, \hat{y}^{1}\right),\left(x^{2}, \hat{y}^{2}\right) \ldots,\left(x^{\mathrm{N}}, \hat{y}^{\mathrm{N}}\right)\right\}
{(x1,y^1),(x2,y^2)…,(xN,y^N)}

我们希望找到一个 F ( x , y ) F(x,y) F(x,y) ,使得 F ( x 1 , y 1 ) F(x^1,y^1) F(x1,y1)必须比其他所有的 F ( x 1 , y ) F(x^1,y) F(x1,y) 的值大,同理 F ( x 2 , y 2 ) F(x^2,y^2) F(x2,y2)必须比其他所有的 F ( x 2 , y ) F(x^2,y) F(x2,y)的值大,以此类推…。
在之后的课程里面,我们集中在Q3,假设已经知道怎么抽 ϕ ( x , y ) ϕ(x,y) ϕ(x,y),Q2里已经解决了如何算 y ~ \tilde{y} y~ 。
Outline(大纲)

Separable case(可分情形)
也就是SVM里面提到过的,数据是线性可分的,也就是说存在一个权重向量
x
^
\hat{x}
x^使得:
w
^
⋅
ϕ
(
x
1
,
y
^
1
)
≥
w
^
⋅
ϕ
(
x
1
,
y
)
+
δ
w
^
⋅
ϕ
(
x
2
,
y
^
2
)
≥
w
^
⋅
ϕ
(
x
2
,
y
)
+
δ
\begin{aligned} \hat{w} \cdot \phi\left(x^{1}, \hat{y}^{1}\right) & \geq \hat{w} \cdot \phi\left(x^{1}, y\right)+\delta \\ \hat{w} \cdot \phi\left(x^{2}, \hat{y}^{2}\right) & \geq \hat{w} \cdot \phi\left(x^{2}, y\right)+\delta \end{aligned}
w^⋅ϕ(x1,y^1)w^⋅ϕ(x2,y^2)≥w^⋅ϕ(x1,y)+δ≥w^⋅ϕ(x2,y)+δ
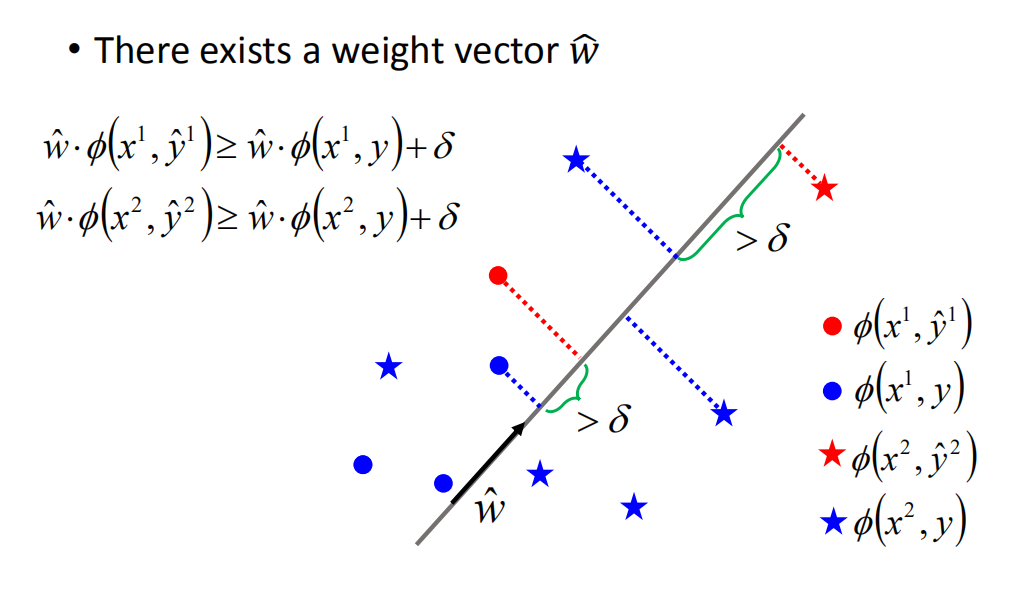
其中,红色代表正确的特征点(feature point),蓝色代表错误的特征点(feature point),可分性可以理解为,我们需要找到一个权值向量,其作用是与 ϕ(x, y) 做内积(inner product) ,能够将正确的point比蓝色的point的值均大于一个 δ \delta δ。
Structured Perceptron(结构化感知机)

-
输入:训练数据集
{ ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) … , ( x N , y ^ N ) } \left\{\left(x^{1}, \hat{y}^{1}\right),\left(x^{2}, \hat{y}^{2}\right) \ldots,\left(x^{\mathrm{N}}, \hat{y}^{\mathrm{N}}\right)\right\} {(x1,y^1),(x2,y^2)…,(xN,y^N)} -
输出:权值向量w
-
算法:
-
初始化 w = 0 w=0 w=0
-
do
-
对于每一个数据样本 ( x n , y ^ n ) (x^n,\hat{y}^n) (xn,y^n)(按照顺序或者随便取都可以):
-
找一个 y ~ n \tilde{y}^n y~n让 a r g max y ∈ Y w ⋅ ϕ ( x n , y ) arg \max\limits_{y∈Y}w·\phi(x^n,y) argy∈Ymaxw⋅ϕ(xn,y)的值最大(Q2,假设已经解决):
y ~ n = a r g max y ∈ Y w ⋅ ϕ ( x n , y ) \tilde{y}^n=arg \max\limits_{y∈Y}w·\phi(x^n,y) y~n=argy∈Ymaxw⋅ϕ(xn,y) -
如果 y ~ n \tilde{y}^n y~n和正确的值 y ^ n \hat{y}^n y^n 不一样,那就更新 w w w:
w → w + ϕ ( x n , y ^ n ) − ϕ ( x n , y ~ n ) w \rightarrow w+\phi(x^n,\hat{y}^n)-\phi(x^n,\tilde{y}^n) w→w+ϕ(xn,y^n)−ϕ(xn,y~n)
更新方式为 w w w + 正确 y ^ n \hat{y}^n y^n 形成的特征向量 ϕ ( x n , y ^ n ) \phi(x^n,\hat{y}^n) ϕ(xn,y^n) - 当前最大的特征向量 ϕ ( x n , y ~ n ) \phi(x^n,\tilde{y}^n) ϕ(xn,y~n),就是让 w w w跟正确的
向量靠近得近一点,跟错误的向量远离一点
-
-
-
看完所有数据之后, w w w都没有更新的话,也就是说对所有数据来说, a r g max arg \max argmax得到的结果都是各自的 y ^ \hat{y} y^的话,这个 w w w就是我们要的
-
这个算法很简单,问题就是我们不知道到底要花多久才会收敛。
更新次数
结论

在argmaxargmax中的 y y y非常多,真的能很轻易的找到红点,跟蓝色点分开吗?
结论是可以的,在可分情形下,在可分情形下,为了得到 w ^ \hat{w} w^,我们最多只需更新 ( R / δ ) 2 (R / \delta)^{2} (R/δ)2次。其中:
- δ \delta δ 为间隔(使得误分的点和正确的点能够线性分离),
- R为 ϕ ( x , y ) \phi(x, y) ϕ(x,y) 与 ϕ ( x , y ′ ) \phi(x, y′) ϕ(x,y′)的最大距离(即特征之间最大的距离)
所以算法需要的信息,与y的空间大小无关!不管蓝色的点有多少个,都不会影响我们需要更新的次数。
证明
证明只需要更新 ( R / δ ) 2 (R/δ)^2 (R/δ)2次

每次发现一笔错误的时候,就会更新一次w。如果你找出来的arg max是 y ^ \hat{y} y^ 就不会被更新,只有 y ~ ≠ y ^ \tilde{y} ≠ \hat{y} y~=y^时才会被更新。
上图
w
0
=
0
→
w
1
→
w
2
→
…
…
→
w
k
→
w
k
+
1
→
…
…
w^{0}=0 \rightarrow w^{1} \rightarrow w^{2} \rightarrow \ldots \ldots \rightarrow w^{k} \rightarrow w^{k+1} \rightarrow \ldots \ldots
w0=0→w1→w2→……→wk→wk+1→……是w更新的演化过程,我们检查
w
k
,
w
k
−
1
w^k,w^{k-1}
wk,wk−1之间的关系,一定会有:
w
k
=
w
k
−
1
+
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
~
n
)
)
(1)
w^{k}=w^{k-1}+\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, \widetilde{y}^{n}\right)) \tag{1}
wk=wk−1+ϕ(xn,y^n)−ϕ(xn,y
n))(1)
提醒一下:
这里考虑的是可分情形。
- 也就是说存在 w ^ \hat{w} w^
- 在所有的数据(任意n)上
- 使得正确的 y ^ \hat{y} y^的值 ≥ 所有非正确y的值 + δ δ δ
- 如上图最下方所示
不失一般性的可以假设 w ^ \hat{w} w^ 的长度为1,如果我们可以找到一个w让我们的数据可分离,那么对w做标准化,让它的长度变为1,还是一样可以让数据可分离。

正式开始证明:
首先看一件事情,看
w
^
\hat{w}
w^和
w
k
w^k
wk之间的关系,如果去计算它们之间的夹角
β
k
\beta_k
βk,会发现当k越来越大时,夹角
β
k
\beta_k
βk越来越小。可以算
c
o
s
β
k
cos\beta_k
cosβk来观察夹角大小:
cos
ρ
k
=
w
^
∥
w
^
∥
⋅
w
k
∥
w
k
∥
\cos \rho_{k}=\frac{\hat{w}}{\|\hat{w}\|} \cdot \frac{w^{k}}{\left\|w^{k}\right\|}
cosρk=∥w^∥w^⋅∥wk∥wk
假定存在一个权值向量 w ^ \hat{w} w^使得
∀
n
\forall n
∀n,所有的样本:
∀
y
∈
Y
−
{
y
^
n
}
\forall y \in Y-\left\{\hat{y}^{n}\right\}
∀y∈Y−{y^n},对于一个样本的所有不正确的标记;
w
^
⋅
ϕ
(
x
n
,
y
^
n
)
≥
w
^
⋅
ϕ
(
x
n
,
y
)
+
δ
\hat{w} \cdot \phi\left(x^{n}, \hat{y}^{n}\right) \geq \hat{w} \cdot \phi\left(x^{n}, y\right)+\delta
w^⋅ϕ(xn,y^n)≥w^⋅ϕ(xn,y)+δ
不失一般性,假设
∥
w
^
∥
=
1
\|\widehat{w}\|=1
∥w
∥=1
w
^
⋅
w
k
=
w
^
⋅
(
w
k
−
1
+
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
~
n
)
)
=
w
^
⋅
w
k
−
1
+
w
^
⋅
ϕ
(
x
n
,
y
^
n
)
−
w
^
⋅
ϕ
(
x
n
,
y
~
n
)
(2)
\begin{aligned} \hat{w} \cdot w^{k} &=\hat{w} \cdot\left(w^{k-1}+\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, \widetilde{y}^{n}\right)\right) \\ &=\hat{w} \cdot w^{k-1}+\hat{w} \cdot \phi\left(x^{n}, \hat{y}^{n}\right)-\hat{w} \cdot \phi\left(x^{n}, \widetilde{y}^{n}\right) \end{aligned} \tag{2}
w^⋅wk=w^⋅(wk−1+ϕ(xn,y^n)−ϕ(xn,y
n))=w^⋅wk−1+w^⋅ϕ(xn,y^n)−w^⋅ϕ(xn,y
n)(2)
在可分情形下,有
w
^
⋅
ϕ
(
x
n
,
y
^
n
)
−
w
^
⋅
ϕ
(
x
n
,
y
~
n
)
≥
δ
(3)
\hat{w} \cdot \phi\left(x^{n}, \hat{y}^{n}\right)-\hat{w} \cdot \phi\left(x^{n}, \widetilde{y}^{n}\right)\geq \delta \tag{3}
w^⋅ϕ(xn,y^n)−w^⋅ϕ(xn,y
n)≥δ(3)
从而由公式(2)和公式(3)可以得到:
w
^
⋅
w
k
≥
w
^
⋅
w
k
−
1
+
δ
\hat{w} \cdot w^{k} \geq \hat{w} \cdot w^{k-1}+\delta
w^⋅wk≥w^⋅wk−1+δ
进一步推导:
w
^
⋅
w
1
≥
δ
w
^
⋅
w
2
≥
2
δ
.
.
.
.
.
.
w
^
⋅
w
k
≥
k
δ
\hat{w} \cdot w^{1} \geq \delta\\\hat{w} \cdot w^{2} \geq 2\delta \\......\\\hat{w} \cdot w^{k} \geq k\delta
w^⋅w1≥δw^⋅w2≥2δ......w^⋅wk≥kδ
最后我们可以得到:
w
^
⋅
w
k
≥
k
δ
\hat{w} \cdot w^{k} \geq k\delta
w^⋅wk≥kδ
也就是说
c
o
s
β
k
cos \beta_k
cosβk的分子是随着k的增大而增大的,但是光分子变大并不能说明夹角变小,例如:

分子变大,很可能是造成向量的长度变长,这个时候的夹角并没有变化!

因此我们还要看
c
o
s
β
k
cos \beta_k
cosβk的分母 。分母中,
∣
∣
w
^
∣
∣
=
1
||\hat{w}||=1
∣∣w^∣∣=1,所以只要考虑
∣
∣
w
k
∣
∣
||w^k||
∣∣wk∣∣就可以,如果
∣
∣
w
k
∣
∣
||w^k||
∣∣wk∣∣不变,且分子变大,那么夹角就能证明是变小的拉。根据公式(1):
∥
w
k
∥
2
=
∥
w
k
−
1
+
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
~
n
)
∣
2
=
∥
w
k
−
1
∥
2
+
∥
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
~
n
)
∥
2
+
2
w
k
−
1
⋅
(
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
~
n
)
)
(4)
\begin{aligned} \left\|w^{k}\right\|^{2} & =\| w^{k-1}+\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left.\left(x^{n}, \widetilde{y}^{n}\right)\right|^{2}\\ & =\left\|w^{k-1}\right\|^{2}+\left\|\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, \widetilde{y}^{n}\right)\right\|^{2}+2 w^{k-1} \cdot\left(\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, \widetilde{y}^{n}\right)\right) \end{aligned} \tag{4}
∥∥wk∥∥2=∥wk−1+ϕ(xn,y^n)−ϕ(xn,y
n)∣2=∥∥wk−1∥∥2+∥ϕ(xn,y^n)−ϕ(xn,y
n)∥2+2wk−1⋅(ϕ(xn,y^n)−ϕ(xn,y
n))(4)
其中,
∥
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
~
n
)
2
∣
∣
>
0
\| \phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, \widetilde{y}^{n}\right)^{2}|| \gt 0
∥ϕ(xn,y^n)−ϕ(xn,y
n)2∣∣>0
这个没什么问题,就相当于是距离,肯定是大于0的,主要是后面那一项;
2
w
k
−
1
⋅
(
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
~
n
)
)
<
0
2 w^{k-1} \cdot\left(\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, \widetilde{y}^{n}\right)\right)\lt0
2wk−1⋅(ϕ(xn,y^n)−ϕ(xn,y
n))<0
这里是因为算法中规定,只有
ϕ
(
x
n
,
y
^
n
)
\phi\left(x^{n}, \hat{y}^{n}\right)
ϕ(xn,y^n)小于
ϕ
(
x
n
,
y
~
n
)
\phi\left(x^{n}, \widetilde{y}^{n}\right)
ϕ(xn,y
n)才会有更新动作,这里既然是出于更新中,所以这项小于0。
假设两个特征
ϕ
(
x
n
,
y
^
n
)
\phi\left(x^{n}, \hat{y}^{n}\right)
ϕ(xn,y^n)和
ϕ
(
x
n
,
y
~
n
)
\phi\left(x^{n}, \widetilde{y}^{n}\right)
ϕ(xn,y
n) 的最大距离是
R
R
R,公式(4)可以写为:
∥
w
k
∥
2
≤
∥
w
k
−
1
∥
2
+
R
2
\left\|w^{k}\right\|^{2} \leq\left\|w^{k-1}\right\|^{2}+\mathrm{R}^{2}
∥∥wk∥∥2≤∥∥wk−1∥∥2+R2
我们假设任意两个特征向量之间的距离小于R,并且
w
w
w的初始值
w
0
=
0
w^0=0
w0=0,则有:
∥
w
1
∥
2
≤
∥
w
0
∥
2
+
R
2
=
R
2
∥
w
2
∥
2
≤
∥
w
1
∥
2
+
R
2
≤
2
R
2
.
.
.
.
.
.
∥
w
k
∥
2
≤
k
R
2
\left\|w^{1}\right\|^{2} \leq\left\|w^{0}\right\|^{2}+\mathrm{R}^{2}=\mathrm{R}^{2}\\ \left\|w^{2}\right\|^{2} \leq\left\|w^{1}\right\|^{2}+\mathrm{R}^{2}\leq2\mathrm{R}^{2}\\ ......\\ \left\|w^{k}\right\|^{2} \leq k\mathrm{R}^{2}
∥∥w1∥∥2≤∥∥w0∥∥2+R2=R2∥∥w2∥∥2≤∥∥w1∥∥2+R2≤2R2......∥∥wk∥∥2≤kR2
最后我们可以得到:
∥
w
k
∥
2
≤
k
R
2
\left\|w^{k}\right\|^{2} \leq k\mathrm{R}^{2}
∥∥wk∥∥2≤kR2
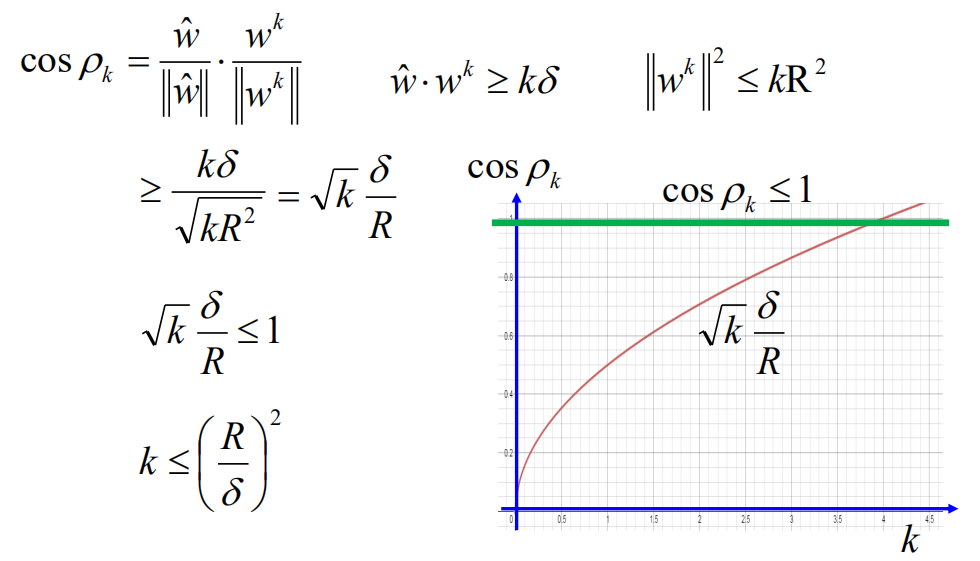
我们上面推导出了两个结论:
w
^
⋅
w
k
≥
k
δ
∥
w
k
∥
2
≤
k
R
2
\hat{w} \cdot w^{k} \geq k \delta \qquad \left\|w^{k}\right\|^{2} \leq k \mathrm{R}^{2}
w^⋅wk≥kδ∥∥wk∥∥2≤kR2
则带入
cos
ρ
k
\cos \rho_{k}
cosρk的式子中,可以得到:
cos
ρ
k
=
w
^
∥
w
^
∥
⋅
w
k
∥
w
k
∥
≥
k
δ
k
R
2
=
k
δ
R
≤
1
\cos \rho_{k}=\frac{\hat{w}}{\|\hat{w}\|} \cdot \frac{w^{k}}{\left\|w^{k}\right\|} \geq \frac{k \delta}{\sqrt{k R^{2}}}=\sqrt{k} \frac{\delta}{R} \leq 1
cosρk=∥w^∥w^⋅∥wk∥wk≥kR2kδ=kRδ≤1
即:
k
≤
(
R
δ
)
2
k \leq\left(\frac{R}{\delta}\right)^{2}
k≤(δR)2
就得到我们的结论最多更新
(
R
δ
)
2
\left(\frac{R}{\delta}\right)^{2}
(δR)2 次
How to make training fast?(如何快速训练?)
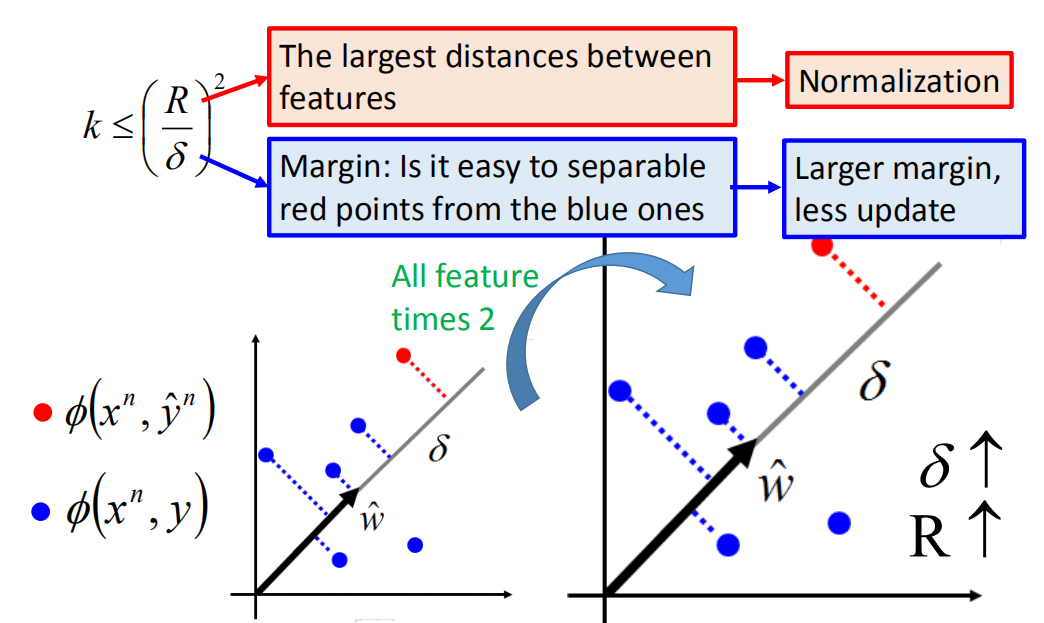
从 k ≤ ( R δ ) 2 k \leq\left(\frac{R}{\delta}\right)^{2} k≤(δR)2我们发现,如果 δ δ δ越大,那么更新次数越少,你可能为了让训练快一点,会想个方法让 δ δ δ增加。你会想说找一组好的特征,可以让红色的圈圈跟蓝色的圈圈分得比较开,你让所有的特征乘以2,相当于上图最下方的图放大2倍,这样 ϕ \phi ϕ就直接增加了2倍。但是这样并不会让学习变快,因为R同时也增加了2倍。所以单纯放大是没用的,要真的去挪动点的位置。
Non-separable case(不可分情形)
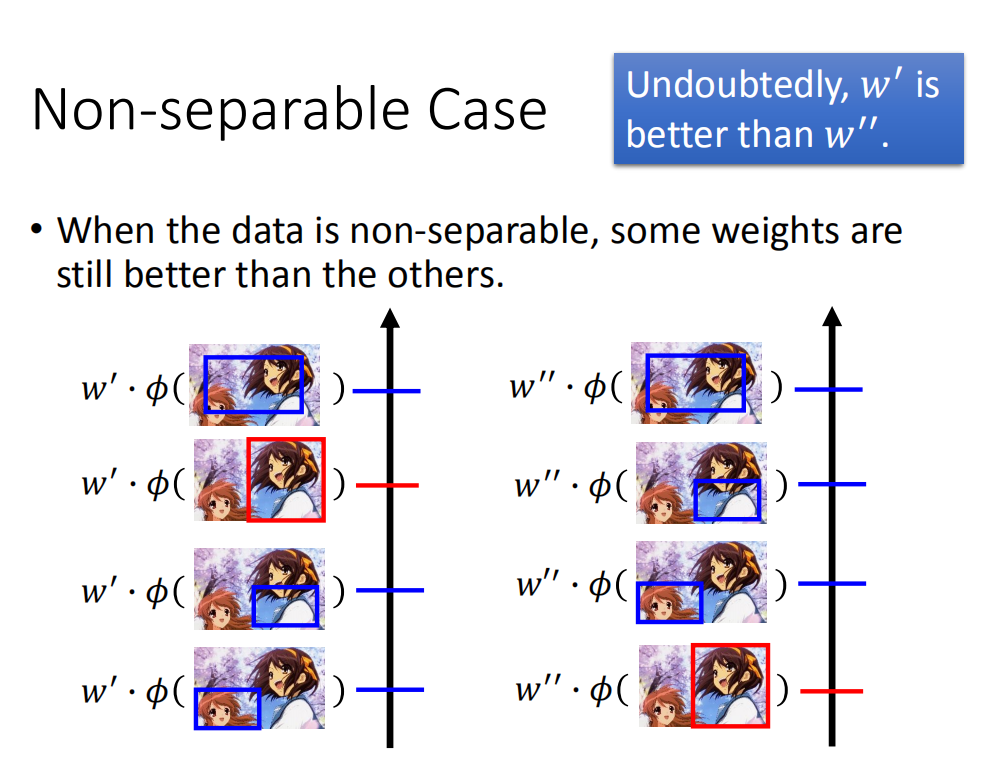
不可分情形要考虑的是,虽然没有任何一个向量可以让正确答案和错误答案被正确分开,但是在这些向量里面,我们还是可以区分出好坏,鉴别出高下。
比如有一个 w ′ w′ w′,可以把正确答案排在第二名,有另外一个 w ′ ′ w′′ w′′,把正确答案排在最后一名。虽然 w ′ , w ′ ′ w',w'' w′,w′′都没有办法让正确答案高过所有其他答案,但是 w ′ w′ w′明显更好。所以在不可分情形下, 还是可以定义一些评估方法来看 w w w是好是坏。
Defining Cost Function(定义成本函数)
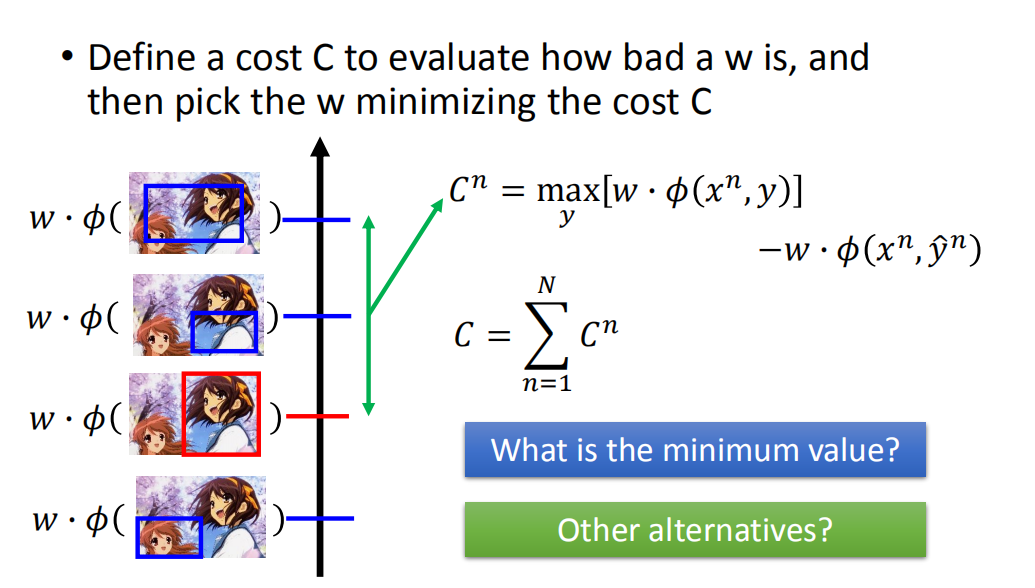
定义一个成本函数C来评估w的效果有多差,然后选择w,从而最小化成本函数C。
关于
C
n
C^n
Cn,就是第n笔数据
x
n
x^n
xn 的cost,意思是:给定的w,在所有的y里面,找到使得
w
⋅
ϕ
(
x
n
,
y
)
w ⋅ ϕ ( x^n , y )
w⋅ϕ(xn,y)最大的值:
max
y
w
⋅
ϕ
(
x
n
,
y
)
\max\limits_{y}w\cdot \phi(x^n,y)
ymaxw⋅ϕ(xn,y)
然后减去正确
y
^
n
\hat{y}^n
y^n的
w
⋅
ϕ
(
x
n
,
y
^
n
)
w\cdot\phi(x^n,\hat{y}^n)
w⋅ϕ(xn,y^n)的值:
C
n
=
max
y
w
⋅
ϕ
(
x
n
,
y
)
−
w
⋅
ϕ
(
x
n
,
y
^
n
)
C^n =\max\limits_{y}w\cdot \phi(x^n,y)-w\cdot\phi(x^n,\hat{y}^n)
Cn=ymaxw⋅ϕ(xn,y)−w⋅ϕ(xn,y^n)
这里
C
n
C^n
Cn 最小值是0;因为它的值不可能是负的,如果max就是正确的,相减最小为0。
为什么是减去正确 y ^ n \hat{y}^n y^n的 w ⋅ ϕ ( x n , y ^ n ) w\cdot\phi(x^n,\hat{y}^n) w⋅ϕ(xn,y^n)的值,因为之前上节课的假设中我们已经假定这个值我们会算,所以顺其自然的用这个值了,如果你要用最正确的前三个值也可以,但是你不会求这三个值,会很麻烦。
把所有的cost累加起来就是
C
C
C:
C
=
∑
n
=
1
N
C
n
C = \sum_{n=1}^N C^n
C=n=1∑NCn
(Stochastic) Gradient Descent((随机)梯度下降法)

虽然cost函数中有一个max操作,是不可导的,但是还是可以梯度下降的,例如之前激活函数ReLU虽然在0点不可导,还不是可以反向传播。
目标是:Find
w
w
w minimizing the cost C :
C
=
∑
n
=
1
N
C
n
C
n
=
max
y
w
⋅
ϕ
(
x
n
,
y
)
−
w
⋅
ϕ
(
x
n
,
y
^
n
)
C= \sum_{n=1}^NC^n \\ C^n =\max\limits_{y}w\cdot \phi(x^n,y)-w\cdot\phi(x^n,\hat{y}^n)
C=n=1∑NCnCn=ymaxw⋅ϕ(xn,y)−w⋅ϕ(xn,y^n)
-
当w不同时,y也会发生改变(在w的二维空间下,被max切割后的效果);
-
求解C的梯度 ▽ C n \bigtriangledown C^n ▽Cn,只需要求解 ϕ \phi ϕ 之间的差值即可:
▽ C n = ϕ ( x n , y ) − ϕ ( x n , y ^ n ) \bigtriangledown C^n = \phi(x^n,y) - \phi(x^n,\hat{y}^n) ▽Cn=ϕ(xn,y)−ϕ(xn,y^n) -
最后利用SGD(随机梯度下降法)更新参数w。
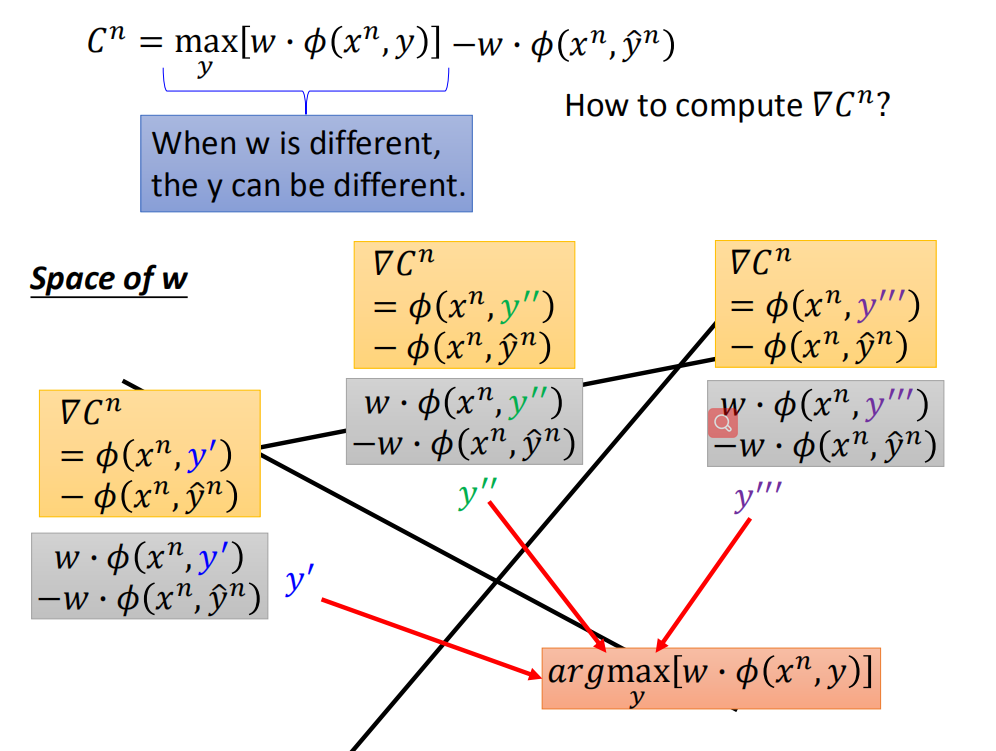
想象上图最下方是w形成的空间,被max切割成好几块。这里是二维平面,那么w就是二维的向量。
- 当 w w w在最左边区域的时候 max y w ⋅ ϕ ( x n , y ) \max\limits_{y}w\cdot \phi(x^n,y) ymaxw⋅ϕ(xn,y)的取值是 y ′ y' y′
- 当 w w w在最中间区域的时候 max y w ⋅ ϕ ( x n , y ) \max\limits_{y}w\cdot \phi(x^n,y) ymaxw⋅ϕ(xn,y)的取值是 y ′ ′ y'' y′′
- 当 w w w在最右边区域的时候 max y w ⋅ ϕ ( x n , y ) \max\limits_{y}w\cdot \phi(x^n,y) ymaxw⋅ϕ(xn,y)的取值是 y ′ ′ ′ y''' y′′′
因此在每个区域中的 C n C^n Cn也可以很好算出来:
- 当 w w w在最左边区域的时候 C n = max y w ⋅ ϕ ( x n , y ′ ) − w ⋅ ϕ ( x n , y ^ n ) C^n =\max\limits_{y}w\cdot \phi(x^n,y')-w\cdot\phi(x^n,\hat{y}^n) Cn=ymaxw⋅ϕ(xn,y′)−w⋅ϕ(xn,y^n)
- 当 w w w在最中间区域的时候 C n = max y w ⋅ ϕ ( x n , y ′ ′ ) − w ⋅ ϕ ( x n , y ^ n ) C^n =\max\limits_{y}w\cdot \phi(x^n,y'')-w\cdot\phi(x^n,\hat{y}^n) Cn=ymaxw⋅ϕ(xn,y′′)−w⋅ϕ(xn,y^n)
- 当 w w w在最右边区域的时候 C n = max y w ⋅ ϕ ( x n , y ′ ′ ′ ) − w ⋅ ϕ ( x n , y ^ n ) C^n =\max\limits_{y}w\cdot \phi(x^n,y''')-w\cdot\phi(x^n,\hat{y}^n) Cn=ymaxw⋅ϕ(xn,y′′′)−w⋅ϕ(xn,y^n)
这三个区域中的边界部分不可以微分,但是在中间的区域都是可以微分的,因此,三个区域对 w w w进行微分后求梯度 ▽ C n \bigtriangledown C^n ▽Cn变成:
- 当 w w w在最左边区域的时候 ▽ C n = ϕ ( x n , y ′ ) − ϕ ( x n , y ^ n ) \bigtriangledown C^n = \phi(x^n,y') - \phi(x^n,\hat{y}^n) ▽Cn=ϕ(xn,y′)−ϕ(xn,y^n)
- 当 w w w在最中间区域的时候 ▽ C n = ϕ ( x n , y ′ ′ ) − ϕ ( x n , y ^ n ) \bigtriangledown C^n = \phi(x^n,y'') - \phi(x^n,\hat{y}^n) ▽Cn=ϕ(xn,y′′)−ϕ(xn,y^n)
- 当 w w w在最右边区域的时候 ▽ C n = ϕ ( x n , y ′ ′ ′ ) − ϕ ( x n , y ^ n ) \bigtriangledown C^n = \phi(x^n,y''') - \phi(x^n,\hat{y}^n) ▽Cn=ϕ(xn,y′′′)−ϕ(xn,y^n)
那么整个算法的流程如下图所示:
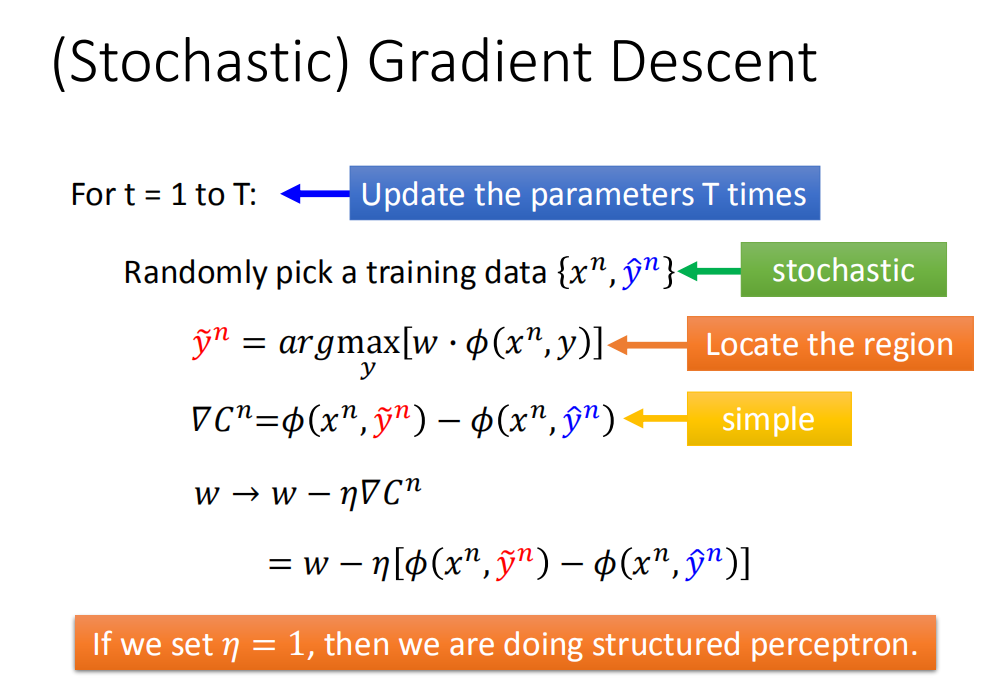
-
For t=1 to T:
-
每次都随机抽取一个样本 { x n , y ^ n } \{x^n,\hat{y}^n\} {xn,y^n}:
-
首先要知道落在哪个区域里面(当前w下),算出来是在 y ~ n \tilde{y}^n y~n区域里面:
y ~ n = a r g max y [ w ⋅ ϕ ( x n , y ) ] \tilde{y}^n = arg \max\limits_{y}[w\cdot \phi(x^n,y)] y~n=argymax[w⋅ϕ(xn,y)] -
计算梯度:
▽ C n = ϕ ( x n , y ~ n ) − ϕ ( x n , y ^ n ) \bigtriangledown C^n = \phi(x^n,\tilde{y}^n) - \phi(x^n,\hat{y}^n) ▽Cn=ϕ(xn,y~n)−ϕ(xn,y^n) -
更新w:
w → w − η ▽ C n = w − η [ ϕ ( x n , y ~ n ) − ϕ ( x n , y ^ n ) ] w \rightarrow w - \eta\bigtriangledown C^n = w-\eta[\phi(x^n,\tilde{y}^n) - \phi(x^n,\hat{y}^n)] w→w−η▽Cn=w−η[ϕ(xn,y~n)−ϕ(xn,y^n)]
-
-
这里也注意两点:
- 当学习率设为1时,就转换为经典的结构化感知机;
- 当设置不同的学习率,将会产生不同的模型。
Considering Errors(考虑误差)
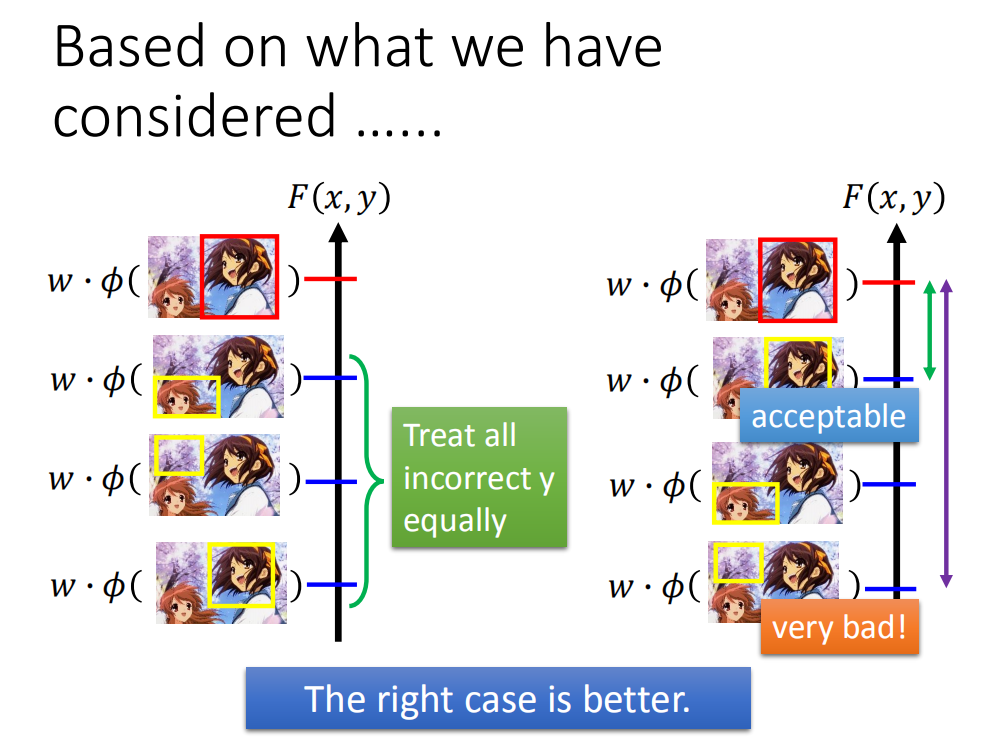
要修改下我们的误差函数,在之前的误差函数里,对我们来说所有错误都是一视同仁的,事实上错误并不是同等地位的。
在结构化学习的例子里面,output有很多的可能,有一些output跟正确的很接近。比如上图右边,正确的是红色框框,如果output是第二个框框(也是框在凉宫春日脸上),你对这个结果也是可以接受的,但是框在下面两个框框上你就不能接受了。所以不同的错误之间还是有差别的(错误有不同的等级),我们应该把这件事考虑进去。比如框在樱花树上,那结果是非常差的,我会希望它的分数特别低,而框在凉宫春日脸上(有些地方没框好),其实结果也是可以接受的,希望跟正确的分数比较接近。如果有另外一个w,不仅能把正确的放在第一位,还可以让那些可以接受的结果分数比较高,错的很离谱的结果分数很低,那显然这个w更好。这样的ww还有一个好处,得到的结果是比较安全的,假如testing跟trainging数据是有一些差距的,就算第一名不是正确的,也可以保证和正确的不会有太大偏差。
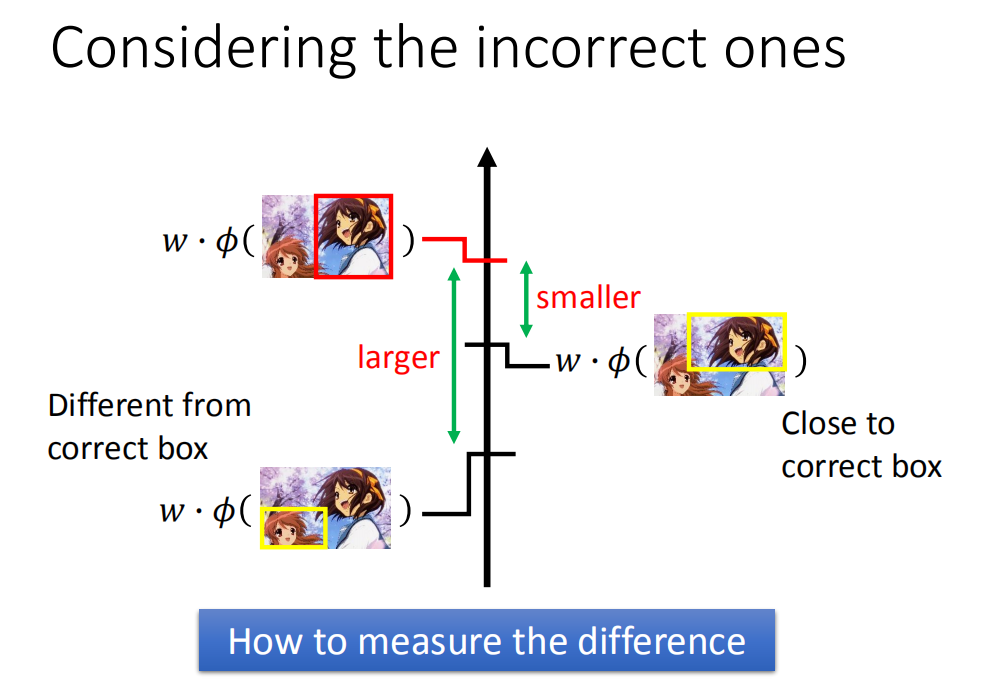
怎么把不同误差不同等级考虑到误差函数里呢?
一个可能的想法说,如上图红色框框是正确的,两个黄色框框是错误的,但是第二个错误的框框和正确的很像,会希望分数差距比较小。反之有个框框(上图第三个)错得很离谱,会希望分数和正确的分数差距比较大。
Defining Error Function(定义误差函数)
现在的问题就变成,如何考虑Error,或者说如何来衡量计算结果与正确结果之间的差距(difference)?
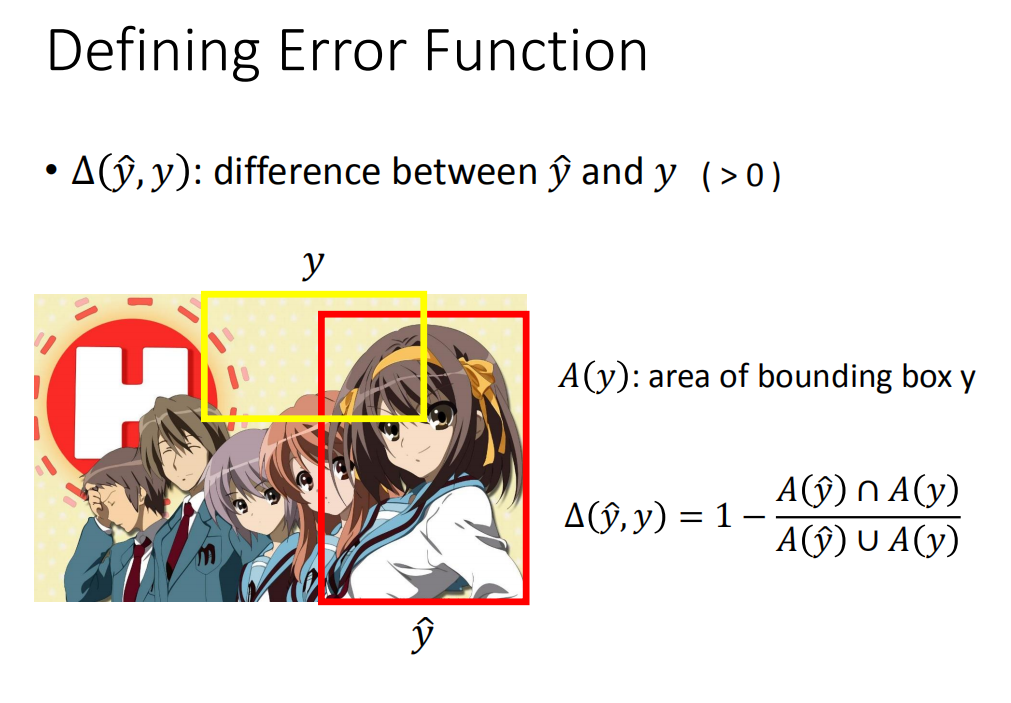
这件事情其实也是取决task的,不同task你要想办法自己定义。
我们的定义
△
(
y
^
,
y
)
\triangle(\hat{y},y)
△(y^,y)为误差的函数,至于到底什么样子要自己定义。以下讨论我们假设
△
\triangle
△是一个正值,如果是自己对自己,那么
△
\triangle
△就是0,常见的做法把
△
\triangle
△定义成上图右下方所示:
△
(
y
^
,
y
)
=
1
−
A
(
y
^
)
∩
A
(
y
)
A
(
y
^
)
∪
A
(
y
)
\triangle(\hat{y},y) = 1 - \frac{A(\hat{y})∩A(y)}{A(\hat{y})∪A(y)}
△(y^,y)=1−A(y^)∪A(y)A(y^)∩A(y)
A
(
y
)
A(y)
A(y)代表
y
y
y框框的面积,如果两个框框的面积交集很小,那么
△
\triangle
△就接近1,交集很大,
△
\triangle
△接近0。
Another Cost Function(其它的成本函数)
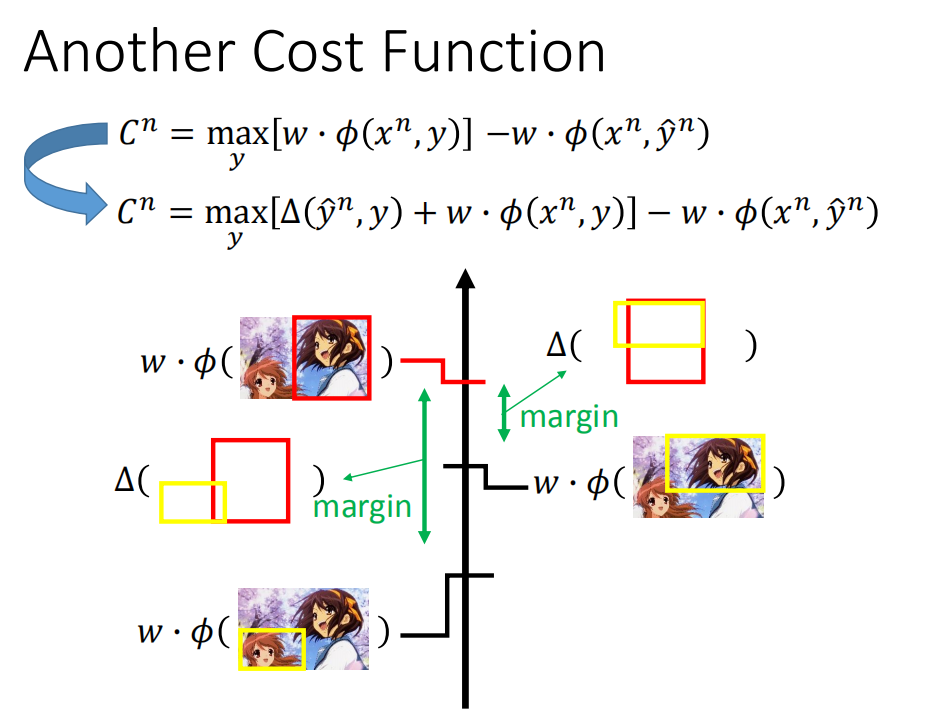
有了 △ \triangle △ 之后,怎么修改成本函数?
本来的成本函数
C
N
C^N
CN计算时,是取分数最高的y
C
n
=
max
y
[
w
⋅
ϕ
(
x
n
,
y
)
]
−
w
⋅
ϕ
(
x
n
,
y
^
n
)
\begin{array}{l}{C^{n}=\max _{y}\left[w \cdot \phi\left(x^{n}, y\right)\right]-w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)}\end{array}
Cn=maxy[w⋅ϕ(xn,y)]−w⋅ϕ(xn,y^n)
现在不是取分数最大,而是要分数
+
△
+\triangle
+△最大,
△
\triangle
△也可以叫做Margin:
C
n
=
max
y
[
Δ
(
y
^
n
,
y
)
+
w
⋅
ϕ
(
x
n
,
y
)
]
−
w
⋅
ϕ
(
x
n
,
y
^
n
)
{C^{n}=\max _{y}\left[\Delta\left(\hat{y}^{n}, y\right)+w \cdot \phi\left(x^{n}, y\right)\right]-w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)}
Cn=ymax[Δ(y^n,y)+w⋅ϕ(xn,y)]−w⋅ϕ(xn,y^n)
思想就是:如果max中找出来的 y 的
△
\triangle
△值很大,那么为了使
C
n
C^n
Cn越小,就会希望
w
⋅
ϕ
(
x
n
,
y
)
w\cdotϕ(x^n,y)
w⋅ϕ(xn,y)越小(跟正确答案的分数差的越远),反之如果有个y 跟正确框框很像的话(
△
\triangle
△值很小),分数就会更接近正确的分数。加上
△
\triangle
△让错误的框框分数离正确的越远,而让可以接受的框框分数变化比错误的远小,这样就拉大了两者之间跟正确分数的差距,就让错误的更错,稍微正确的没有那么错。
Gradient Descent(梯度下降)

为了和之前没有考虑Error的梯度求解区分开来,之前用的是 y ~ \tilde{y} y~,这里用 y ˉ \bar{y} yˉ,具体过程如下:
-
For t=1 to T:
-
每次都随机抽取一个样本 { x n , y ^ n } \{x^n,\hat{y}^n\} {xn,y^n}:
-
首先要知道落在哪个区域里面(当前w下),算出来是在 y ~ n \tilde{y}^n y~n区域里面:
y ˉ n = a r g max y [ △ ( y ^ n , y ) + w ⋅ ϕ ( x n , y ) ] \bar{y}^n = arg \max\limits_{y}[\triangle(\hat{y}^n,y)+w\cdot \phi(x^n,y)] yˉn=argymax[△(y^n,y)+w⋅ϕ(xn,y)] -
计算梯度:
▽ C n = ϕ ( x n , y ˉ n ) − ϕ ( x n , y ^ n ) \bigtriangledown C^n = \phi(x^n,\bar{y}^n) - \phi(x^n,\hat{y}^n) ▽Cn=ϕ(xn,yˉn)−ϕ(xn,y^n) -
更新w:
w → w − η ▽ C n = w − η [ ϕ ( x n , y ˉ n ) − ϕ ( x n , y ^ n ) ] w \rightarrow w - \eta\bigtriangledown C^n = w-\eta[\phi(x^n,\bar{y}^n) - \phi(x^n,\hat{y}^n)] w→w−η▽Cn=w−η[ϕ(xn,yˉn)−ϕ(xn,y^n)]
-
-
Another Viewpoint(其他观点)

之前的成本函数有另外一个观点用来解释。之前的成本函数 C n C^n Cn 是你在训练数据上的误差的上界,当你去最小化有间隔的成本函数时,你是在最小化训练数据的误差上界,虽然最小化训练误差上界不代表误差一定会减小,但是也是有可能会跟着变小的。
假设不正确的函数如上图右上方所示,拿 y ~ \tilde{y} y~ 当做output,希望最小化的成本函数是 C ′ C′ C′( y ^ , y ~ \hat{y},\tilde{y} y^,y~ 差距之和),那我们希望找到一个w,让 C ′ C′ C′越小越好。但是最小化 C ′ C′ C′并没有那么容易,因为 △ \triangle △ 可以是任何函数,想想看就算一个函数在某些地方不可微,总体上也还是可以使用梯度下降的,但是如果 △ \triangle △比那些某些地方不可微的函数还要复杂,比如阶梯状函数,那么梯度下降就完全没用了。
这样 C n C^n Cn就派上用场了, C n C^n Cn是 C ′ C′ C′的上界,那么就找w来最小化 C n C^n Cn,进而间接去最小化 C ′ C′ C′。
那么如何证明 C C C是误差函数之和 C ′ C' C′的上界呢?

我们要证明的就是:
△
(
y
^
n
,
y
~
n
)
≤
C
n
\triangle (\hat{y}^n,\tilde{y}^n) \le C^n
△(y^n,y~n)≤Cn
证明开始:
由于:
w
⋅
ϕ
(
x
m
,
y
~
n
)
−
w
⋅
ϕ
(
x
n
,
y
^
n
)
≥
0
w\cdot \phi(x^m,\tilde{y}^n) - w\cdot\phi(x^n,\hat{y}^n) \ge 0
w⋅ϕ(xm,y~n)−w⋅ϕ(xn,y^n)≥0
我们可以得到下列不等式:
△
(
y
^
n
,
y
~
n
)
≤
△
(
y
^
n
,
y
~
n
)
+
[
w
⋅
ϕ
(
x
m
,
y
~
n
)
−
w
⋅
ϕ
(
x
n
,
y
^
n
)
]
\triangle (\hat{y}^n,\tilde{y}^n) \le \triangle (\hat{y}^n,\tilde{y}^n) +[w\cdot \phi(x^m,\tilde{y}^n) - w\cdot\phi(x^n,\hat{y}^n)]
△(y^n,y~n)≤△(y^n,y~n)+[w⋅ϕ(xm,y~n)−w⋅ϕ(xn,y^n)]
运用结合律,可以得到:
More Cost Functions(更多成本函数的证明)

Δ ( y ^ n , y ~ n ) ≤ C n \Delta\left(\hat{y}^{n}, \tilde{y}^{n}\right) \leq C^{n} Δ(y^n,y~n)≤Cn
-
Margin Rescaling(间隔调整),就是我们上面的解决方案:
C n = max y [ Δ ( y ^ n , y ) + w ⋅ ϕ ( x n , y ) ] − w ⋅ ϕ ( x n , y ^ n ) C^{n}=\max _{y}\left[\Delta\left(\hat{y}^{n}, y\right)+w \cdot \phi\left(x^{n}, y\right)\right]-w \cdot \phi\left(x^{n}, \hat{y}^{n}\right) Cn=ymax[Δ(y^n,y)+w⋅ϕ(xn,y)]−w⋅ϕ(xn,y^n) -
Slack Variable Rescaling(松弛变量调整):
C n = max y Δ ( y ^ n , y ) [ 1 + w ⋅ ϕ ( x n , y ) − w ⋅ ϕ ( x n , y ^ n ) ] C^{n}=\max _{y} \Delta\left(\hat{y}^{n}, y\right)\left[1+w \cdot \phi\left(x^{n}, y\right)-w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)\right] Cn=ymaxΔ(y^n,y)[1+w⋅ϕ(xn,y)−w⋅ϕ(xn,y^n)]这个方法的大概思想是:y 与 y ^ \hat{y} y^的差距很大, Δ \Delta Δ 也就很大,乘起来之后结果会把差距放大;反之,y 与 y ^ \hat{y} y^的差距很小, Δ \Delta Δ 也就很小,乘起来之后结果也会很小。
另外之前那种用的加法,有缺陷,没有考虑到w 和 Δ \Delta Δ的大小(因为 Δ \Delta Δ自己定义的),例如一个是0.001,一个是1000,那么加法对这个权重上没有考虑清楚,用乘法的话就是自带normalization效果,所以这个方法有它的道理。
Regularization(正则化)
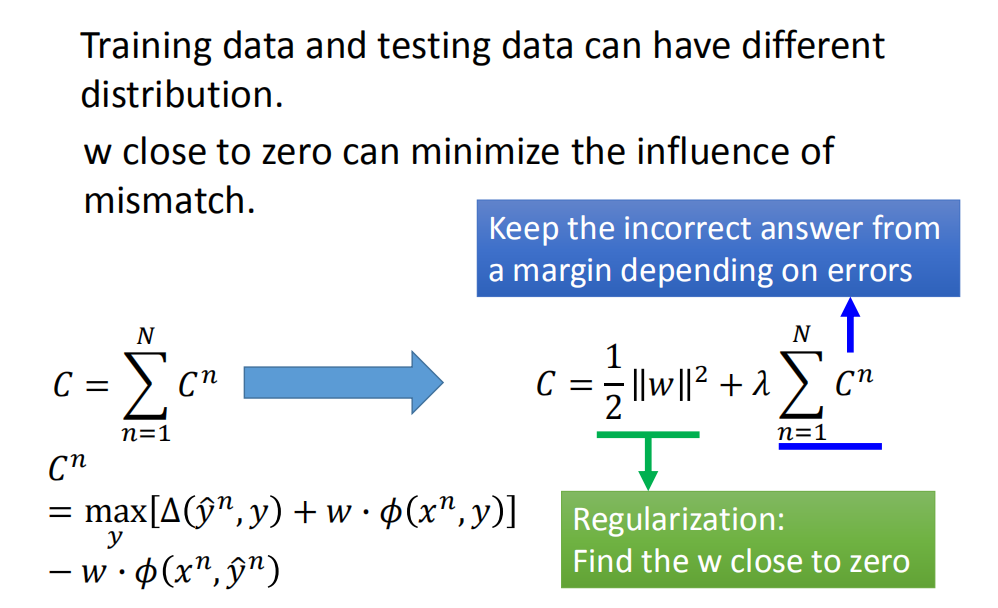
-
训练数据和测试数据可以有不同的分布;
-
如果w与0比较接近,那么我们就可以最小化误差匹配的影响;我们把w接近于0这件事加到成本函数里。也就是说在原来的成本函数里加上w的L2正则。
-
即在原来的基础上,加上一个正则项 1 2 ∥ w ∥ 2 \frac{1}{2}\|w\|^{2} 21∥w∥2,λ为权衡参数;
C = ∑ n = 1 N C n ⇒ C = λ ∑ n = 1 N C n + 1 2 ∥ w ∥ 2 C=\sum_{n=1}^{N} C^{n} \Rightarrow \quad C=\lambda \sum_{n=1}^{N} C^{n}+\frac{1}{2}\|w\|^{2} C=n=1∑NCn⇒C=λn=1∑NCn+21∥w∥2

-
For t=1 to T:
-
每次都随机抽取一个样本 { x n , y ^ n } \{x^n,\hat{y}^n\} {xn,y^n}:
-
首先要知道落在哪个区域里面(当前w下),算出来是在 y ~ n \tilde{y}^n y~n区域里面:
y ˉ n = a r g max y [ △ ( y ^ n , y ) + w ⋅ ϕ ( x n , y ) ] \bar{y}^n = arg \max\limits_{y}[\triangle(\hat{y}^n,y)+w\cdot \phi(x^n,y)] yˉn=argymax[△(y^n,y)+w⋅ϕ(xn,y)] -
计算梯度:
▽ C n = ϕ ( x n , y ˉ n ) − ϕ ( x n , y ^ n ) + w \bigtriangledown C^n = \phi(x^n,\bar{y}^n) - \phi(x^n,\hat{y}^n)+w ▽Cn=ϕ(xn,yˉn)−ϕ(xn,y^n)+w -
更新w:
w → w − η ▽ C n = w − η [ ϕ ( x n , y ˉ n ) − ϕ ( x n , y ^ n ) ] − η w = ( 1 − η ) w − η [ ϕ ( x n , y ˉ n ) − ϕ ( x n , y ^ n ) ] \begin{aligned} w \rightarrow w - \eta\bigtriangledown C^n &= w-\eta[\phi(x^n,\bar{y}^n) - \phi(x^n,\hat{y}^n)]-\eta w \\ &=(1-\eta)w-\eta[\phi(x^n,\bar{y}^n)-\phi(x^n,\hat{y}^n)] \end{aligned} w→w−η▽Cn=w−η[ϕ(xn,yˉn)−ϕ(xn,y^n)]−ηw=(1−η)w−η[ϕ(xn,yˉn)−ϕ(xn,y^n)]
-
-
Structured SVM(结构化支持向量机)
概念介绍
SVM 即支持向量机,常用于二分类模型。它主要的思想是:
-
它是特征空间上间隔最大的线性分类器;
-
对于线性不可分的情况,通过非线性映射算法将低维空间的线性不可分的样本映射到高维特征空间,高维特征空间能够进行线性分析。
什么是结构化?
我们在结构化的介绍中也已经介绍过了!其实机器学习中,如果按照输出空间不同可以分为:
-
二元分类 (binary classification)
-
多元分类 (multiclass classification)
-
回归问题 (regression)
-
结构化预测 (structured prediction)
其中前面三类都是我们常见且经常用的,第四种结构化预测重点体现在结构化上,前面三类的输出都是标签类别或者回归值之类的单变量,而结构化预测输出是一种结构化的数据结构,比如输入一句话,输出是一颗语法树。此外,结构还可以是图结构、序列结构等。
特点:
输入输出都是一种带有结构的对象- 对象:sequence,list,tree,bounding box
结构化 SVM:
结构化 SVM间互相存在依赖关系的结构数据,对传统 SVM 进行了改进,可以说结构化 SVM 是在传统 SVM 的基础上扩展出来的。结构化 SVM 使用时主要涉及学习和推理两个过程,与大多数机器学习算法一样,学习其实就是确定模型的参数的过程,而推理就是根据学习到的模型对给定的输入进行预测的过程,这一点我们在前面也已经介绍了很多了!
公式的三种描述
描述一:
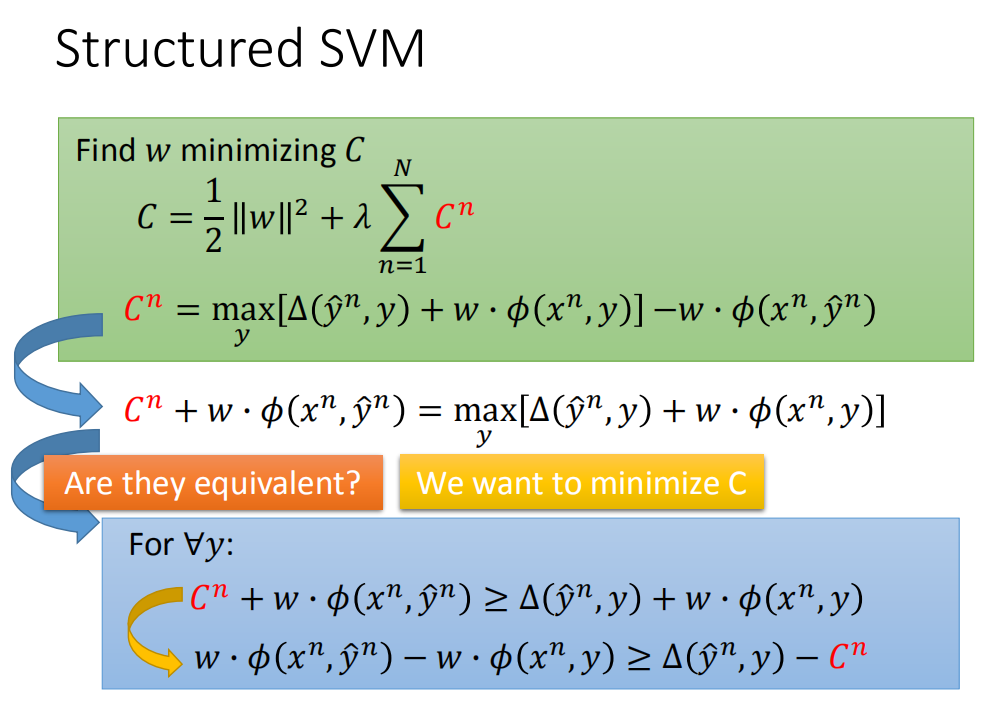
求得w使得C最小化,使得:
C
=
λ
∑
n
=
1
N
C
n
+
1
2
∥
w
∥
2
C=\lambda \sum_{n=1}^{N} C^{n}+\frac{1}{2}\|w\|^{2}
C=λn=1∑NCn+21∥w∥2
其中:
C
n
=
max
y
[
Δ
(
y
^
n
,
y
)
+
w
⋅
ϕ
(
x
n
,
y
)
]
−
w
⋅
ϕ
(
x
n
,
y
^
n
)
C^{n}=\max _{y}\left[\Delta\left(\hat{y}^{n}, y\right)+w \cdot \phi\left(x^{n}, y\right)\right]-w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)
Cn=ymax[Δ(y^n,y)+w⋅ϕ(xn,y)]−w⋅ϕ(xn,y^n)
移项可以得到:
C
n
+
w
⋅
ϕ
(
x
n
,
y
^
n
)
=
max
y
[
Δ
(
y
^
n
,
y
)
+
w
⋅
ϕ
(
x
n
,
y
)
]
(1)
\\C^{n}+w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)=\max _{y}\left[\Delta\left(\hat{y}^{n}, y\right)+w \cdot \phi\left(x^{n}, y\right)\right] \tag{1}
Cn+w⋅ϕ(xn,y^n)=ymax[Δ(y^n,y)+w⋅ϕ(xn,y)](1)
将 max 去掉,我们将式子转换成:
F
o
r
∀
y
:
C
n
+
w
⋅
ϕ
(
x
n
,
y
^
n
)
≥
Δ
(
y
^
n
,
y
)
+
w
⋅
ϕ
(
x
n
,
y
)
(2)
For\ \forall{y} : \ \ {C^{n}+w \cdot \phi\left(x^{n}, \hat{y}^{n}\right) \geq \Delta\left(\hat{y}^{n}, y\right)+w \cdot \phi\left(x^{n}, y\right)} \tag{2}
For ∀y: Cn+w⋅ϕ(xn,y^n)≥Δ(y^n,y)+w⋅ϕ(xn,y)(2)
这里有一个问题:(1)和(2)式是等价的吗?
我们假设:
f
(
x
)
=
max
y
(
y
)
(a)
f(x) = \max\limits_y (y) \tag{a}
f(x)=ymax(y)(a)
如果
y
=
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
y={1,2,3,4,5,6,7,8,9}
y=1,2,3,4,5,6,7,8,9,那么
f
(
x
)
=
9
f(x) = 9
f(x)=9
如果我们直接写成:
f
(
x
)
>
∀
y
(b)
f(x) > \forall y \tag{b}
f(x)>∀y(b)
显然(a)和(b)不等价,因为在(b)中,f ( x ) 可以等于10,11,12,etc。
但是如果我们加上一个约束: m i n i m i z e f ( x ) minimize \ f(x) minimize f(x)
这个时候(a)和(b)就等价了!
根据式子(2)进行一项,可以进一步得到;
w
⋅
ϕ
(
x
n
,
y
^
n
)
−
w
⋅
ϕ
(
x
n
,
y
)
≥
Δ
(
y
^
n
,
y
)
−
C
n
{w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)-w \cdot \phi\left(x^{n}, y\right) \geq \Delta\left(\hat{y}^{n}, y\right)-C^{n}}
w⋅ϕ(xn,y^n)−w⋅ϕ(xn,y)≥Δ(y^n,y)−Cn
描述二:
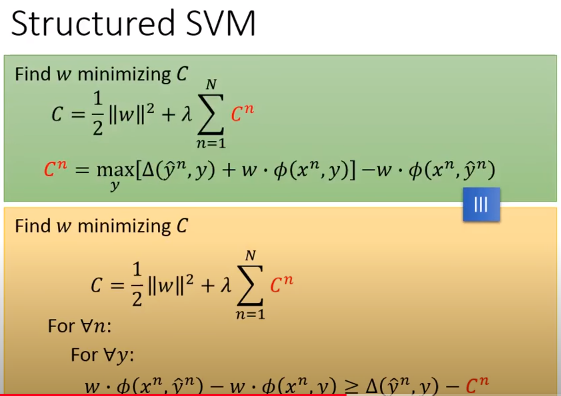
也就是说:
找到
w
w
w去最小化
C
C
C:
C
=
1
2
∣
∣
w
∣
∣
2
+
λ
∑
n
=
1
N
C
n
C = \frac{1}{2}||w||^2 + \lambda \sum_{n=1}^N C^n
C=21∣∣w∣∣2+λn=1∑NCn
对于每一个n的每一个y,即:
F
o
r
∀
n
:
F
o
r
∀
y
:
w
⋅
ϕ
(
x
n
,
y
^
n
)
−
w
⋅
ϕ
(
x
n
,
y
)
≥
Δ
(
y
^
n
,
y
)
−
C
n
\begin{aligned} &For\ \forall n: \\ &\ \ \ \ \ For \ \forall y: \\ &\ \ \ \ \ \ \ {w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)-w \cdot \phi\left(x^{n}, y\right) \geq \Delta\left(\hat{y}^{n}, y\right)-C^{n}} \end{aligned}
For ∀n: For ∀y: w⋅ϕ(xn,y^n)−w⋅ϕ(xn,y)≥Δ(y^n,y)−Cn
描述三:
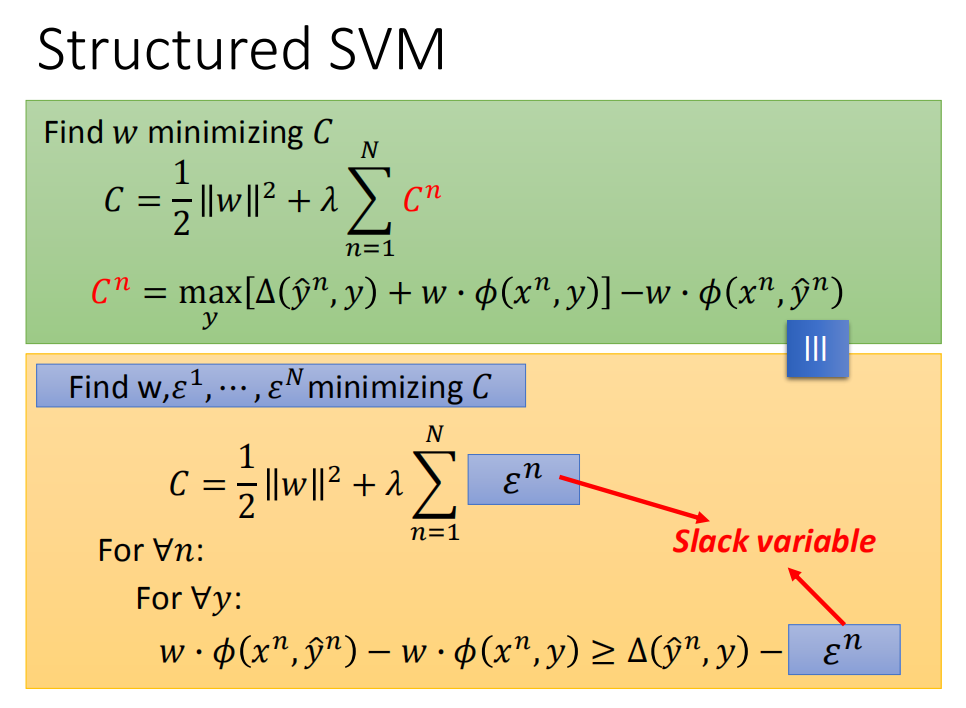
到这里,通常是把C 换成 ϵ \epsilon ϵ(slack variable,中文名:松弛因子),描述2等价于:
找到
w
,
ϵ
1
,
⋯
,
ϵ
N
w,\epsilon^1,\cdots,\epsilon^N
w,ϵ1,⋯,ϵN去最小化
C
C
C:
C
=
1
2
∣
∣
w
∣
∣
2
+
λ
∑
n
=
1
N
ϵ
n
(1)
C = \frac{1}{2}||w||^2 + \lambda \sum_{n=1}^N \epsilon^n \tag{1}
C=21∣∣w∣∣2+λn=1∑Nϵn(1)
对于每一个n的每一个y,即:
F
o
r
∀
n
:
F
o
r
∀
y
:
w
⋅
ϕ
(
x
n
,
y
^
n
)
−
w
⋅
ϕ
(
x
n
,
y
)
≥
Δ
(
y
^
n
,
y
)
−
ϵ
n
(2)
\begin{aligned} &For\ \forall n: \\ &\ \ \ \ \ For \ \forall y: \\ &\ \ \ \ \ \ \ {w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)-w \cdot \phi\left(x^{n}, y\right) \geq \Delta\left(\hat{y}^{n}, y\right)-\epsilon^{n}} \end{aligned} \tag{2}
For ∀n: For ∀y: w⋅ϕ(xn,y^n)−w⋅ϕ(xn,y)≥Δ(y^n,y)−ϵn(2)

对于描述3中的公式(2),如果
y
=
y
^
n
y = \hat{y}^n
y=y^n,有:
w
⋅
(
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
^
n
)
)
=
0
Δ
(
y
^
n
,
y
^
n
)
=
0
w \cdot (\phi(x^n,\hat{y}^n)-\phi(x^n,\hat{y}^n)) = 0 \\ \Delta(\hat{y}^n,\hat{y}^n) = 0
w⋅(ϕ(xn,y^n)−ϕ(xn,y^n))=0Δ(y^n,y^n)=0
进一步进行化简可以得到:
ϵ
n
≥
0
\epsilon^n \ge 0
ϵn≥0
描述3中的公式(2)就等价于:
F
o
r
∀
y
≠
y
^
n
:
w
⋅
ϕ
(
x
n
,
y
^
n
)
−
w
⋅
ϕ
(
x
n
,
y
)
≥
Δ
(
y
^
n
,
y
)
−
ϵ
n
,
ϵ
n
≥
0
\begin{aligned} & For \ \forall y \ne \hat{y}^n: \\ & \ \ \ {w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)-w \cdot \phi\left(x^{n}, y\right) \geq \Delta\left(\hat{y}^{n}, y\right)-\epsilon^{n}}, \ \ \ \epsilon^n \ge 0 \end{aligned}
For ∀y=y^n: w⋅ϕ(xn,y^n)−w⋅ϕ(xn,y)≥Δ(y^n,y)−ϵn, ϵn≥0
Intuition Explanation(直观解释)
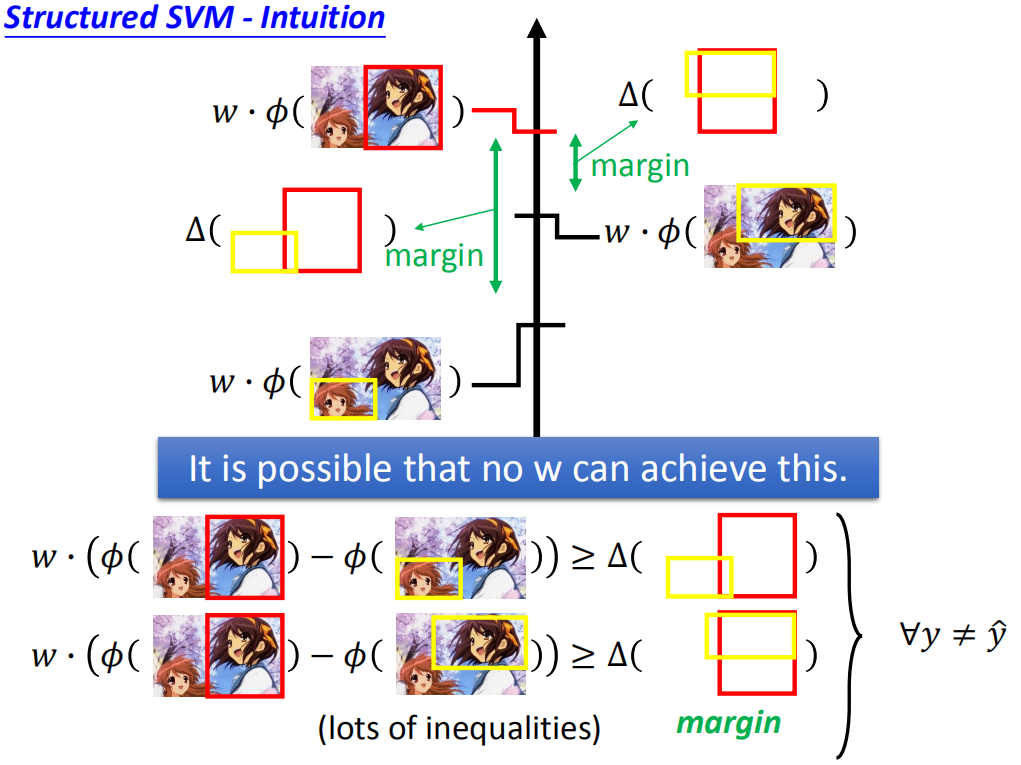
黄框与红框差距越大,它们之间的margin也就是 Δ \Delta Δ也就越大,因此我们要找的参数w要满足下面的条件:

当然黄色的框框不止这两个,还有很多很多个,就是除了正确的红框之外的任意位置都可以有黄框,写成数学表达就是: ∀ y ≠ y ^ \forall y \neq \widehat y ∀y=y ,所以上面的不等式也是有无穷多个。
这样我们就很难找到一个参数w使得所有的不等式都成立。
因此我们想办法把margin变小一点,不用 Δ \Delta Δ来作为margin,而是用: Δ − ε \Delta-\varepsilon Δ−ε来作为margin(注意,使得margin变小是要减去一个正数才可以,否则减去负数就变大了。所以这里默认 ε ≥ 0 \varepsilon\geq0 ε≥0,如果 ε ≤ 0 \varepsilon\leq0 ε≤0会是使得上面的不等式约束更加严格。):
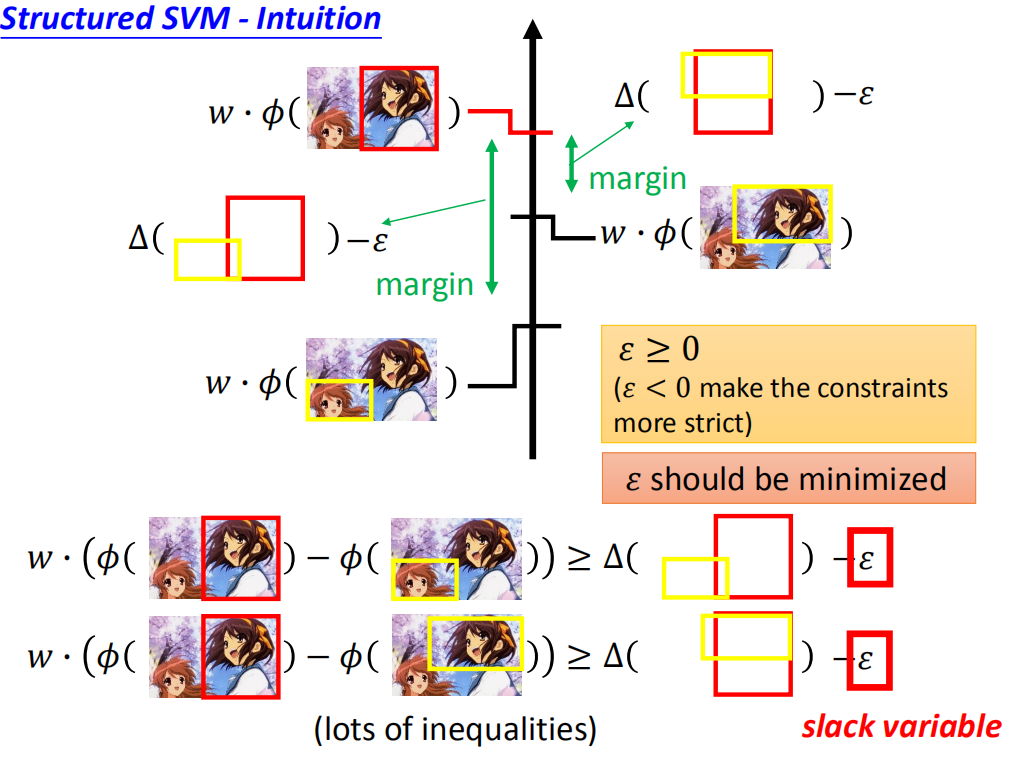
上图中的绿色margin长度应该变小就更加逼真了。。。
由于 ε \varepsilon ε的作用是放宽约束,所以起了一个名字叫松弛因子。我们当然不会希望约束放得太宽,否则margin就失去存在的意义了(例如: ε → ∞ \varepsilon\to\infty ε→∞,margin 就变成了负值,随便一个参数w就能满足条件),因此,我们还加上了一个条件就是 ε \varepsilon ε要最小化。
就好比妹子想找高富帅,这个条件没法找到,她也不会找一个矮矬穷,会想办法找一个高富,高帅,富帅。
下面举例:
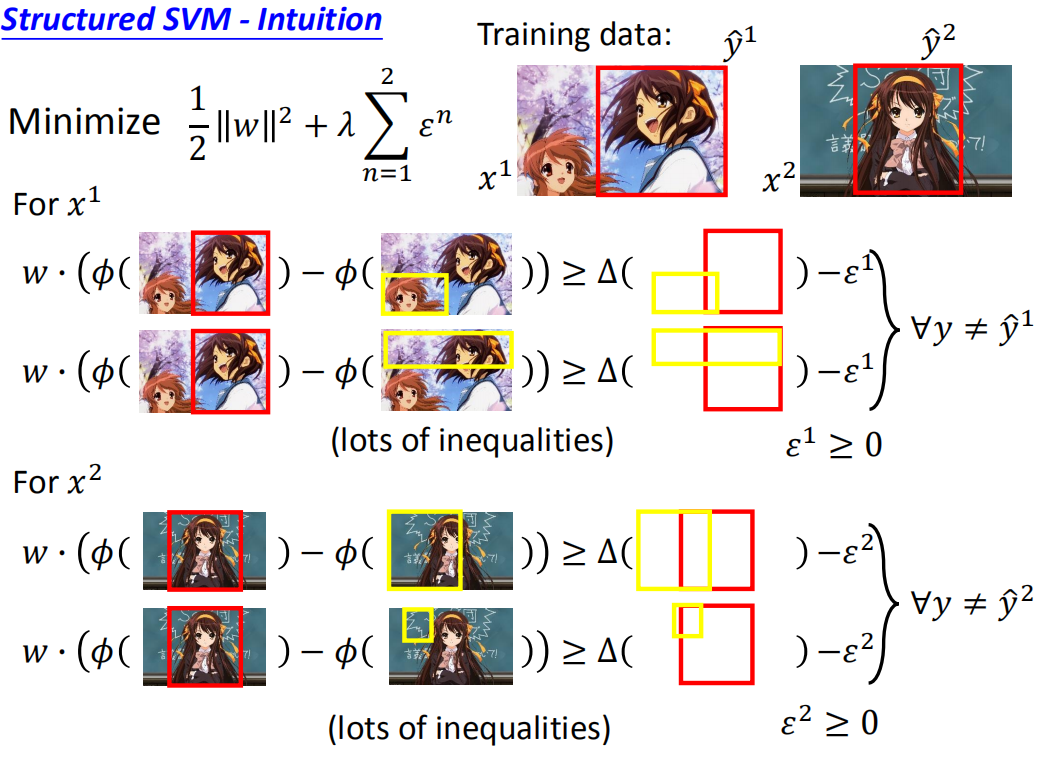
假设,我们现在有两个训练数据:
(
x
1
,
y
^
1
)
和
(
x
2
,
y
^
2
)
\left(x^{1}, \hat{y}^{1}\right) 和 \left(x^{2},\hat{y}^2\right)
(x1,y^1)和(x2,y^2)
对于
x
1
x^{1}
x1而言,我们希望正确的减去错误的,要求大于它们之间的
Δ
\Delta
Δ减去
ε
1
\varepsilon^{1}
ε1,同时满足:
∀
y
≠
y
^
1
且
ε
1
≥
0
\forall y \neq \hat{y}^{1} 且 \varepsilon^{1} \geq 0
∀y=y^1且ε1≥0
同理,对于
x
2
x^{2}
x2而言,一样采用以上方式,我们希望正确的减去错误的,要求大于它们之间的
Δ
\Delta
Δ减去
ε
1
\varepsilon^{1}
ε1,同时满足:
∀
y
≠
y
^
2
且
ε
2
≥
0
\forall y \neq \hat{y}^{2} 且 \varepsilon^{2} \geq 0
∀y=y^2且ε2≥0
在满足以上这些不等式的前提之下,我们希望
1
2
∣
∣
w
∣
∣
2
+
λ
∑
n
=
1
2
ε
n
\frac{1}{2} ||w||^2 + \lambda \sum_{n=1}^{2} \varepsilon^{n}
21∣∣w∣∣2+λn=1∑2εn
是最小的!

换一种说法就是:
找到
w
,
ε
1
,
⋯
,
ε
N
w, \varepsilon^{1}, \cdots, \varepsilon^{N}
w,ε1,⋯,εN,最小化
C
C
C ,其中:
C
=
1
2
∣
∣
w
∣
∣
2
+
λ
∑
n
=
1
2
ε
n
C=\frac{1}{2} ||w||^2 + \lambda \sum_{n=1}^{2} \varepsilon^{n}
C=21∣∣w∣∣2+λn=1∑2εn
在最小化目标函数同时,要求我们满足以下的限制:
对所有的训练样本,以及所有不是正确答案的标记,我们希望,正确答案的分数减去其它标记的分数大于等于正确标记与其它标记之间的差距再减去一个
ε
n
\varepsilon^{n}
εn,同时满足其大于等于0,即
F
o
r
∀
n
:
F
o
r
∀
y
≠
y
^
n
:
w
⋅
(
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
)
)
≥
Δ
(
y
^
n
,
y
)
−
ε
n
,
ε
n
≥
0
\begin{aligned} & For \ \forall n :\\ & \ \ \ \ For \ \forall y \neq \hat{y}^{n}:\\ & \ \ \ \ \ \ \ \ \ w \cdot\left(\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, y\right)\right) \geq \Delta\left(\hat{y}^{n}, y\right)-\varepsilon^{n}, \varepsilon^{n} \geq 0 \end{aligned}
For ∀n: For ∀y=y^n: w⋅(ϕ(xn,y^n)−ϕ(xn,y))≥Δ(y^n,y)−εn,εn≥0
- 可以利用SVM包中的solver来解决以上的问题;
- 是一个二次规划(Quadratic Programming QP)的问题;
- 约束条件过多,需要通过切割平面算法(Cutting Plane Algorithm)解决受限的问题。
Cutting Plane Algorithm for Structured SVM(切割平面算法)
无约束条件的问题求解
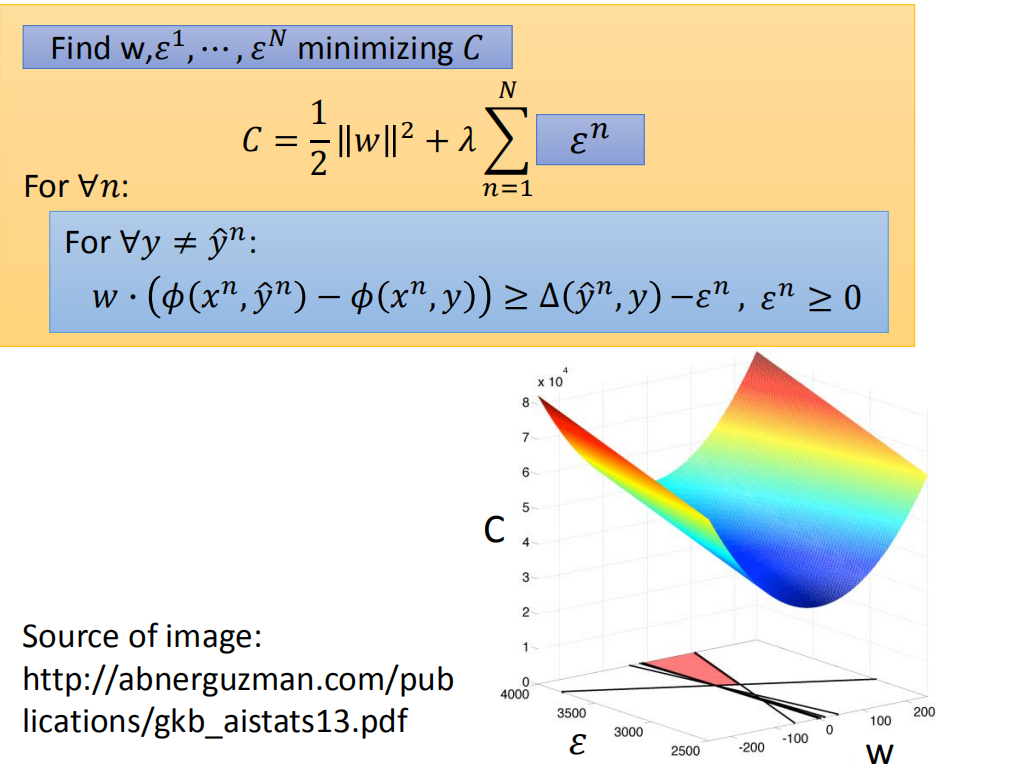
👉 DivMCuts: Faster Training of Structural SVMs with Diverse M-Best Cutting-Planes
假设我们先不考虑限制的部分,只考虑最小化部分,来看一下解的是什么样的问题。
我们只看要最小化的部分,有w和ϵ ,现在假设w只有一维,训练数据只有一笔。在没有约束条件下,最小化就很容易,看起来就像上图右下方图示。
问题是这里有些约束,这些约束是做什么事情?
有约束条件的问题求解
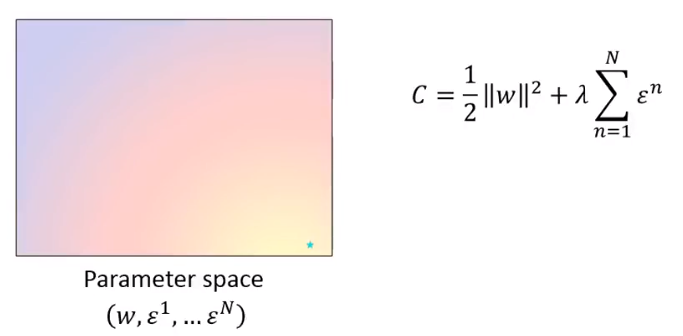
在w和
ε
i
ε^i
εi组成的参数空间中(本来是高维的,这里用二维的平面来做个样例),颜色表示Cost C的值:
C
=
1
2
∥
w
∥
2
+
λ
∑
n
=
1
N
ε
n
C=\frac{1}{2}\|w\|^{2}+\lambda \sum_{n=1}^{N} \varepsilon^{n}
C=21∥w∥2+λn=1∑Nεn
在没有限制的情况下,绿的点对应的是最小值。也就是还没有引入任何约束的时候的Cost C的最小值。
我们现在把之前推导出来的约束加上:
F
o
r
∀
n
:
F
o
r
∀
y
≠
y
^
n
:
w
⋅
(
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
)
)
≥
Δ
(
y
^
n
,
y
)
−
ε
n
,
ε
n
≥
0
\begin{aligned} & For \ \forall n :\\ & \ \ \ \ For \ \forall y \neq \hat{y}^{n}:\\ & \ \ \ \ \ \ \ \ \ w \cdot\left(\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, y\right)\right) \geq \Delta\left(\hat{y}^{n}, y\right)-\varepsilon^{n}, \varepsilon^{n} \geq 0 \end{aligned}
For ∀n: For ∀y=y^n: w⋅(ϕ(xn,y^n)−ϕ(xn,y))≥Δ(y^n,y)−εn,εn≥0
图像变成了:
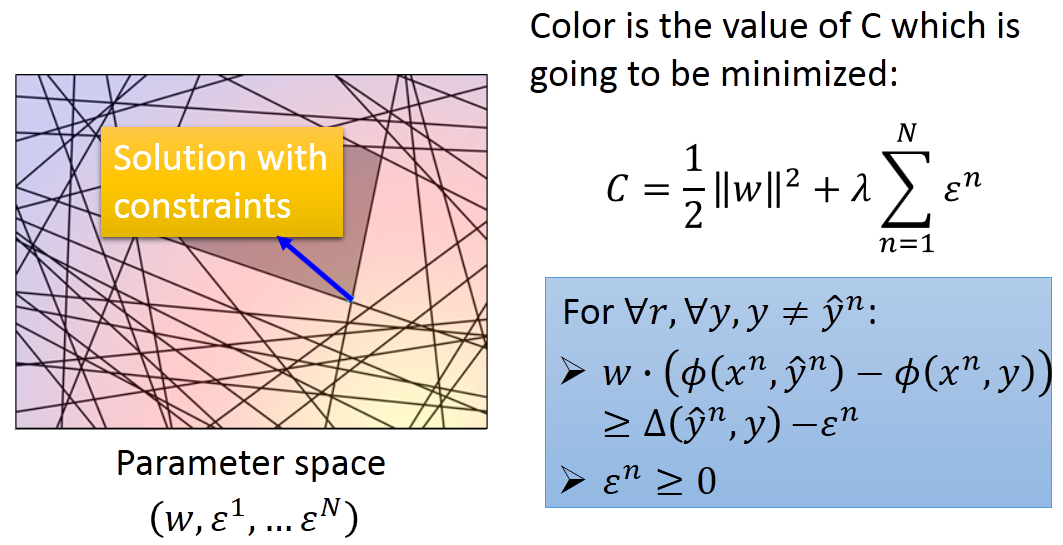
在有限制的情况下,只有中间阴影部分是符合约束条件的,因此需要在该区域内(How如何确定多边形的形状?)寻找最小值。
Cutting Plane Algorithm(算法)
我们观察约束可以看到,虽然约束很多,但是很多约束实际上是冗余的,真正起到决定Cost最小值的是下图中的两条红线,其他约束去掉也不会影响结果:
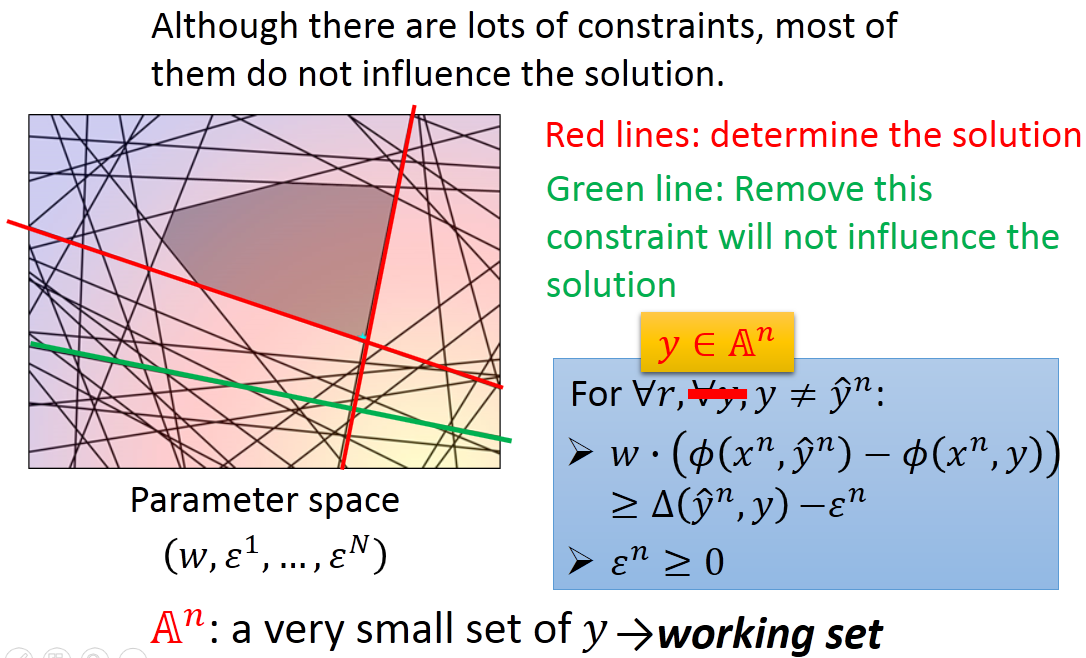
绿线(冗元)表示移除此约束不会影响问题的求解,删除冗元线条,原本是穷举
y
≠
y
^
n
y \neq \hat{y}^{n}
y=y^n,而现在我们需要移除那些不起作用的线条,保留有用的线条,这些有影响的线条集可以理解为Working Set,用
A
n
\mathbb{A}^{n}
An表示(利用迭代法寻找Working Set)。
那么我们的约束条件就变成了;
F
o
r
∀
n
:
F
o
r
y
∈
A
n
,
y
≠
y
^
n
:
w
⋅
(
ϕ
(
x
n
,
y
^
n
)
−
ϕ
(
x
n
,
y
)
)
≥
Δ
(
y
^
n
,
y
)
−
ε
n
,
ε
n
≥
0
\begin{aligned} & For \ \forall n :\\ & \ \ \ \ For \ y ∈A^n, y \neq \hat{y}^{n}:\\ & \ \ \ \ \ \ \ \ \ w \cdot\left(\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, y\right)\right) \geq \Delta\left(\hat{y}^{n}, y\right)-\varepsilon^{n}, \varepsilon^{n} \geq 0 \end{aligned}
For ∀n: For y∈An,y=y^n: w⋅(ϕ(xn,y^n)−ϕ(xn,y))≥Δ(y^n,y)−εn,εn≥0
如果Working set比较小,那么Cost最小值就是有可能解出来的,下面来看如何确定Working set,用的是一个迭代的算法:
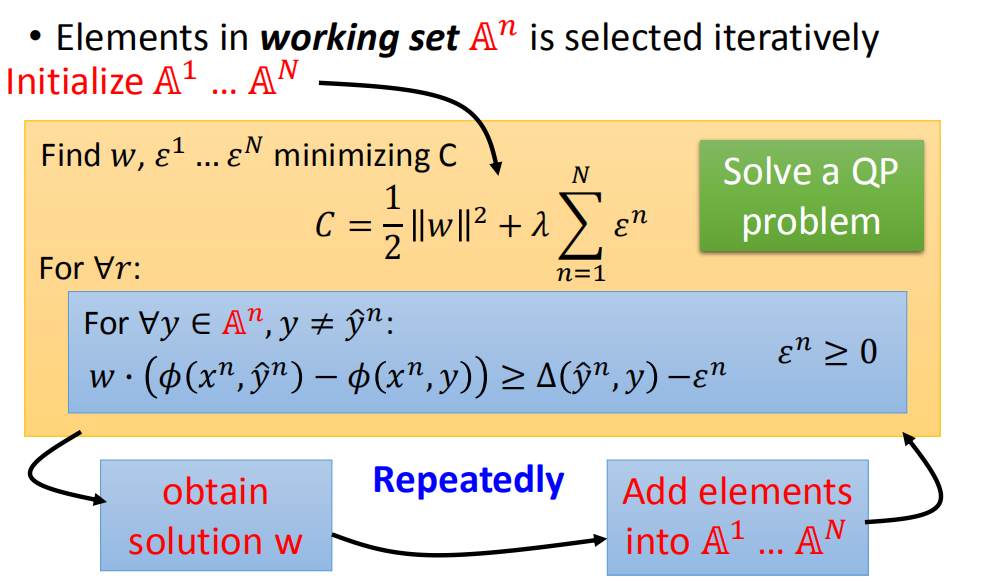
Quadratic Program (QP):凸优化的二次规划问题。
原本解决QP问题,需要考虑所有可能的标记y,但如果给定一组Working Set,我们仅需考虑作用集里的标记y即可;然后再解决QP问题就相对简单多了。
- 对每一个example都初始化它的working set ,初始化 A n : A 1 , A 2 , ⋯ , A N A^n:A^1,A^2,\cdots,A^N An:A1,A2,⋯,AN
- 接下来根据初始化的Working Set,去解这个project programming,本来要考虑所有的y,但是给定一组Working Set后,只要考虑Working Set中的y就可以了。
- 假设根据Working Set解出一个w后,再用这个w去找一些新的成员加到Working Set里
- Working Set变化后再去接project programming,又得到一个不一样的w…不断循环下去,直到w不再变化为止!
下面是图解这个算法如何运作的:
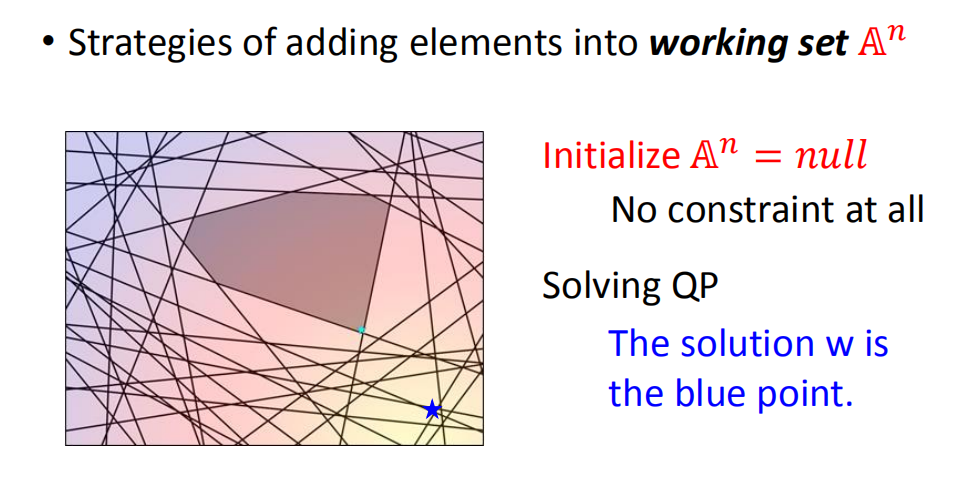
初始化working set A n A^n An,最开始是不考虑约束的,因此 A n = n u l l A^n = null An=null。在没有约束的情况下,求解QP的结果就是w是蓝色这个点。
看看蓝色的点是没有办法满足哪些约束。例如下图中的红色约束:
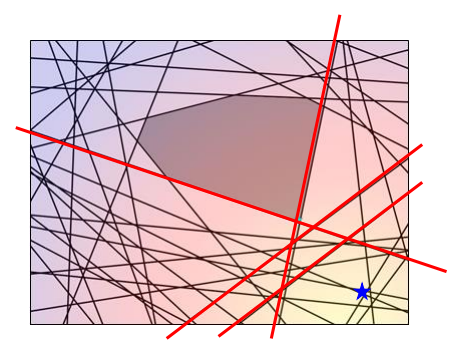
虽然蓝点不满足很多约束,但我们现在只找出没有满足的最“严重的”那一个,这个选择标准后面再解释(应该是按垂直距离)即可:
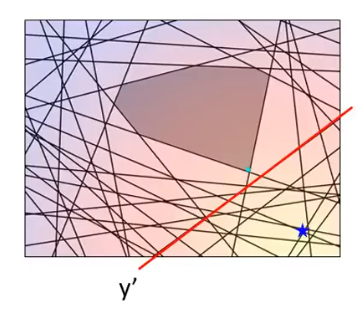
那么我们就把找出来的这个约束记为:
y
′
y'
y′,然后把
y
′
y'
y′加入到working set 中:
A
n
=
A
n
∪
{
y
′
}
=
{
y
′
}
A^n = A^n ∪ \{y'\} = \{y'\}
An=An∪{y′}={y′}
新的working set不再是空的了,里面有东西了,根据新的working set,我们重新算最小值:
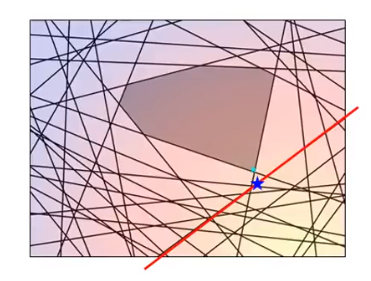
然后再看这个蓝色星星不满足哪些约束:
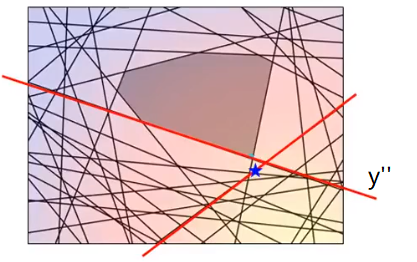
我们把找出来的这个约束记为:
y
′
′
y''
y′′,然后把
y
′
′
y''
y′′加入到working set 中:
A
n
=
A
n
∪
{
y
′
′
}
=
{
y
′
,
y
′
′
}
A^n = A^n ∪ \{y''\} = \{y',y''\}
An=An∪{y′′}={y′,y′′}
下面又重复迭代,根据新的working set计算最小值:
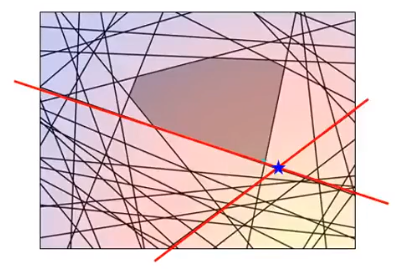
然后再看这个蓝色星星不满足哪些约束:
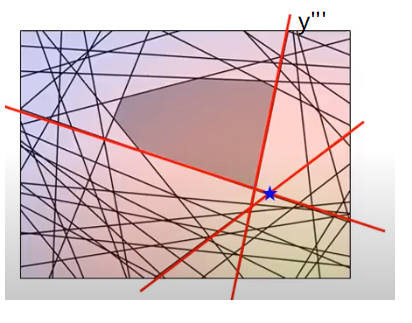
我们把找出来的这个约束记为:
y
′
′
′
y'''
y′′′,然后把
y
′
′
′
y'''
y′′′加入到working set 中:
A
n
=
A
n
∪
{
y
′
′
′
}
=
{
y
′
,
y
′
′
,
y
′
′
′
}
A^n = A^n ∪ \{y'''\} = \{y',y'',y'''\}
An=An∪{y′′′}={y′,y′′,y′′′}
下面又重复迭代,根据新的working set计算最小值:
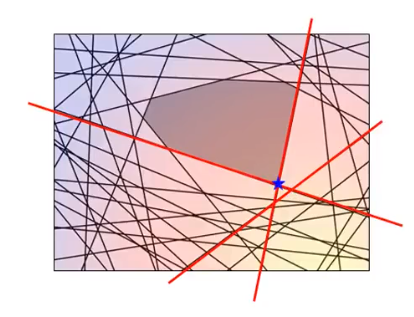
至此,完毕!
Find the most violated one(向有效集中添加元素的策略)
上面挖了个坑,如何找到最小值相对应最不满足的约束条件是什么?现在来填:

常规约束条件:
C
o
n
s
t
r
a
i
n
t
:
w
⋅
(
ϕ
(
x
,
y
^
)
−
ϕ
(
x
,
y
)
)
≥
Δ
(
y
^
,
y
)
−
ε
Constraint: \ \ \ \ \ w \cdot(\phi(x, \hat{y})-\phi(x, y)) \geq \Delta(\hat{y}, y)-\varepsilon
Constraint: w⋅(ϕ(x,y^)−ϕ(x,y))≥Δ(y^,y)−ε
而violated constraint刚好相反:
V
i
o
l
a
t
e
a
C
o
n
t
r
a
i
n
t
:
w
′
⋅
(
ϕ
(
x
,
y
^
)
−
ϕ
(
x
,
y
)
)
<
Δ
(
y
^
,
y
)
−
ε
′
Violate \ a \ Contraint: \ \ \ \ \ w^{\prime} \cdot(\phi(x, \hat{y})-\phi(x, y))<\Delta(\hat{y}, y)-\varepsilon^{\prime}
Violate a Contraint: w′⋅(ϕ(x,y^)−ϕ(x,y))<Δ(y^,y)−ε′
在多数的violated constraints中,我们选定一个标准来衡量violation的程度(偏差越多,violated的越严重):
D
e
g
r
e
e
o
f
V
i
o
l
a
t
i
o
n
:
Δ
(
y
^
,
y
)
−
ε
′
−
w
′
⋅
(
ϕ
(
x
,
y
^
)
−
ϕ
(
x
,
y
)
)
Degree \ of \ Violation: \ \ \ \ \ \Delta(\hat{y}, y)-\varepsilon^{\prime}-w^{\prime} \cdot(\phi(x, \hat{y})-\phi(x, y))
Degree of Violation: Δ(y^,y)−ε′−w′⋅(ϕ(x,y^)−ϕ(x,y))
又因为ε′与
w
′
⋅
ϕ
(
x
,
y
^
)
w^{\prime} \cdot \phi(x, \hat{y})
w′⋅ϕ(x,y^) 是固定值,不影响评价标准,所以上面式子中的这两项可以去掉,从而得到:
D
e
g
r
e
e
o
f
V
i
o
l
a
t
i
o
n
:
Δ
(
y
^
,
y
)
+
w
′
⋅
ϕ
(
x
,
y
)
Degree \ of \ Violation: \ \ \ \ \ \Delta(\hat{y}, y)+w^{\prime} \cdot \phi(x, y)
Degree of Violation: Δ(y^,y)+w′⋅ϕ(x,y)
有了评价标准后,最不满足的就是最大值那个拉:
T
h
e
m
o
s
t
v
i
o
l
a
t
e
d
o
n
e
:
arg
max
y
[
Δ
(
y
^
,
y
)
+
w
⋅
ϕ
(
x
,
y
)
]
The\ most\ violated\ one: \ \ \ \ \arg \max _{y}[\Delta(\hat{y}, y)+w \cdot \phi(x, y)]
The most violated one: argymax[Δ(y^,y)+w⋅ϕ(x,y)]
算法总结


-
给定训练数据集
{ ( x 1 , y ^ 1 ) , ( x 2 , y ^ 2 ) , ⋯ , ( x N , y ^ N ) } \left\{\left(x^{1}, \hat{y}^{1}\right),\left(x^{2}, \hat{y}^{2}\right), \cdots,\left(x^{N}, \hat{y}^{N}\right)\right\} {(x1,y^1),(x2,y^2),⋯,(xN,y^N)} -
每一个pair都有一个Working Set,且初始设定为
A 1 ← null, A 2 ← null, ⋯ , A N ← n u l l \mathbb{A}^{1} \leftarrow \text { null, } \mathbb{A}^{2} \leftarrow \text { null, } \cdots, \mathbb{A}^{N} \leftarrow null A1← null, A2← null, ⋯,AN←null
-
重复以下过程
-
根据已经有的Working set,解一个w
-
根据现在的w,对每一个训练数据 ( x n , y ^ n ) (x^n,\hat{y}^n) (xn,y^n):
-
找出不满足最严重的的约束,用 y ˉ n \bar{y}^n yˉn 表示:
y ˉ n = arg max y [ Δ ( y ^ , y ) + w ⋅ ϕ ( x , y ) ] \bar{y}^n = \arg \max _{y}[\Delta(\hat{y}, y)+w \cdot \phi(x, y)] yˉn=argymax[Δ(y^,y)+w⋅ϕ(x,y)] -
把 y ˉ n \bar{y}^n yˉn 加进Working set:
A n ← A n ∪ { y ‾ n } \mathbb{A}^{n} \leftarrow \mathbb{A}^{n} \cup\left\{\overline{y}^{n}\right\} An←An∪{yn}
-
-
-
直到 A 1 , A 2 , ⋯ , . A N A^1,A^2,\cdots,.A^N A1,A2,⋯,.AN不再改变
-
返回 w w w
示例解释
用目标检测举个例子:
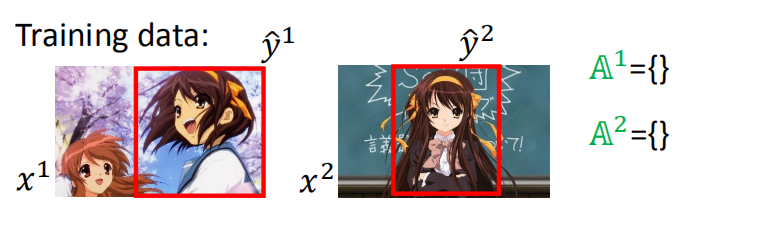
假设,我们现在有两个训练数据: ( x 1 , y ^ 1 ) 和 ( x 2 , y ^ 2 ) \left(x^{1}, \hat{y}^{1}\right) 和 \left(x^{2}, \hat{y}^{2}\right) (x1,y^1)和(x2,y^2)
初始的Working set是:
A
1
=
{
}
A
2
=
{
}
\begin{array}{l}{A^{1}=\{ \}} \\ {A^{2}=\{ \}}\end{array}
A1={}A2={}
无约束的问题解决
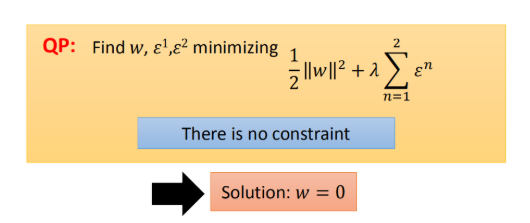
上图的约束少写了: ϵ 1 > 0 , ϵ 2 > 0 \epsilon^1 \gt 0,\epsilon^2\gt0 ϵ1>0,ϵ2>0!
由于没有约束,上面那个式子很容易看出来,当w = 0 w=0的时候,得到最小值。
有约束的问题解决
然后用w = 0去找the most violated的约束。
此时:
A 1 = { } A 2 = { } w = 0 \begin{array}{l}{A^{1}=\{ \}} \\ {A^{2}=\{ \}}\end{array}\\ w=0 A1={}A2={}w=0
y ‾ 1 = arg max y [ Δ ( y ^ 1 , y ) + 0 ⋅ ϕ ( x 1 , y ) ] \overline{y}^{1}=\arg \max _{y}\left[\Delta\left(\hat{y}^{1}, y\right)+0 \cdot \phi\left(x^{1}, y\right)\right] y1=argymax[Δ(y^1,y)+0⋅ϕ(x1,y)]
下面给出六个黄框框
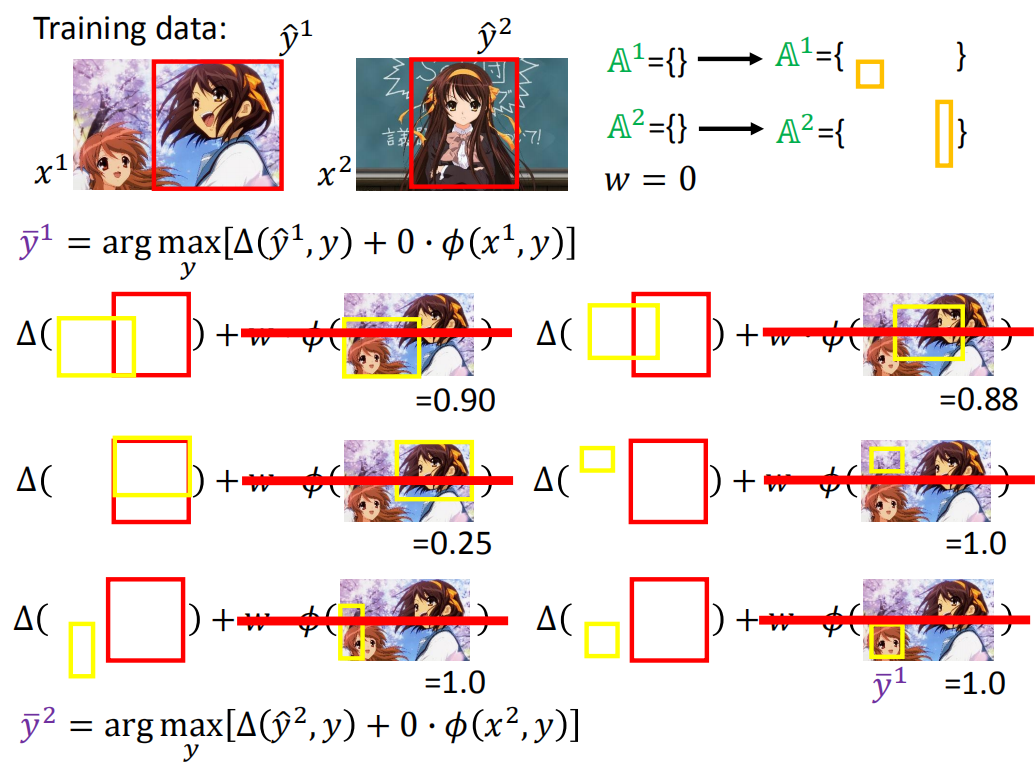
上图由于w = 0 ,当去解violated约束时,也就是求解 arg max y [ Δ ( y ^ 1 , y ) + 0 ⋅ ϕ ( x 1 , y ) ] \arg \max _{y}\left[\Delta\left(\hat{y}^{1}, y\right)+0 \cdot \phi\left(x^{1}, y\right)\right] argmaxy[Δ(y^1,y)+0⋅ϕ(x1,y)]。后面一项为0,所以可以用直接去掉(对应着上图的红杠)。
只剩下 Δ \Delta Δ,这个玩意如果黄框不和红框重叠,值就会很大。看到 Δ \Delta Δ有三个一样的都最大,都是1,我们随便挑一个,右下角那个作为 y ˉ 1 \bar{y}^1 yˉ1。
同样去计算
y
2
y^2
y2对应的:
y
‾
2
=
arg
max
y
[
Δ
(
y
^
2
,
y
)
+
0
⋅
ϕ
(
x
2
,
y
)
]
\overline{y}^{2}=\arg \max _{y}\left[\Delta\left(\hat{y}^{2}, y\right)+0 \cdot \phi\left(x^{2}, y\right)\right]
y2=argymax[Δ(y^2,y)+0⋅ϕ(x2,y)]
将
y
ˉ
1
,
y
ˉ
2
\bar{y}^1,\bar{y}^2
yˉ1,yˉ2加入到working set中得到:

然后用新的working set解决下图QP问题(下图中的working set中有两个约束),计算得到 w = w 1 w = w^1 w=w1
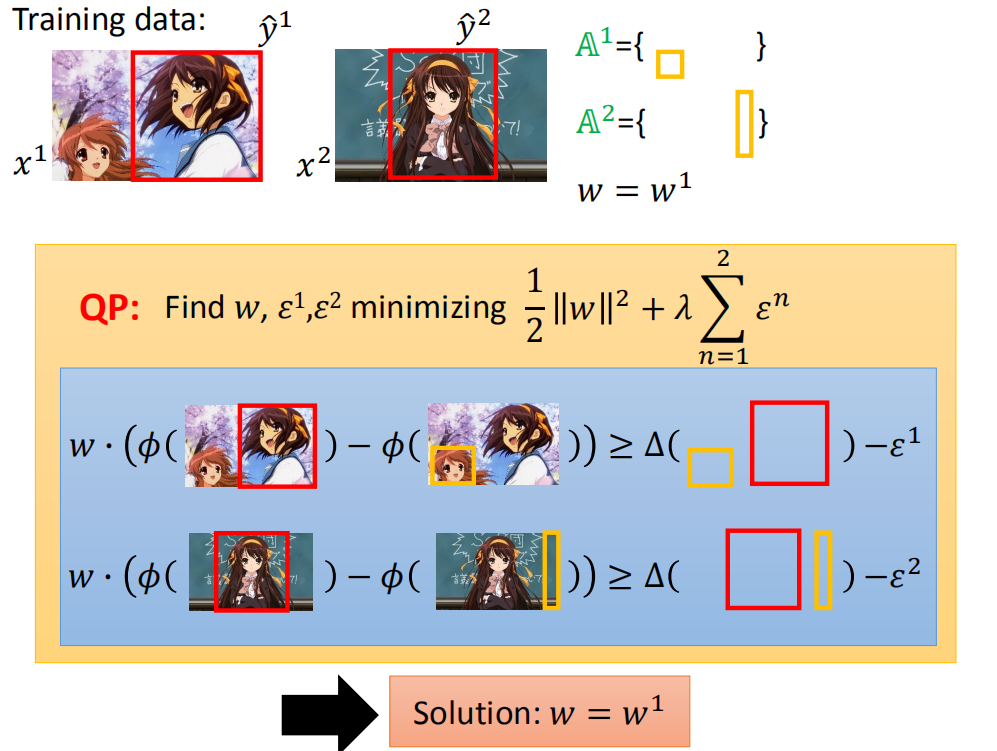
用 w 1 w^1 w1去找the most violated的约束。
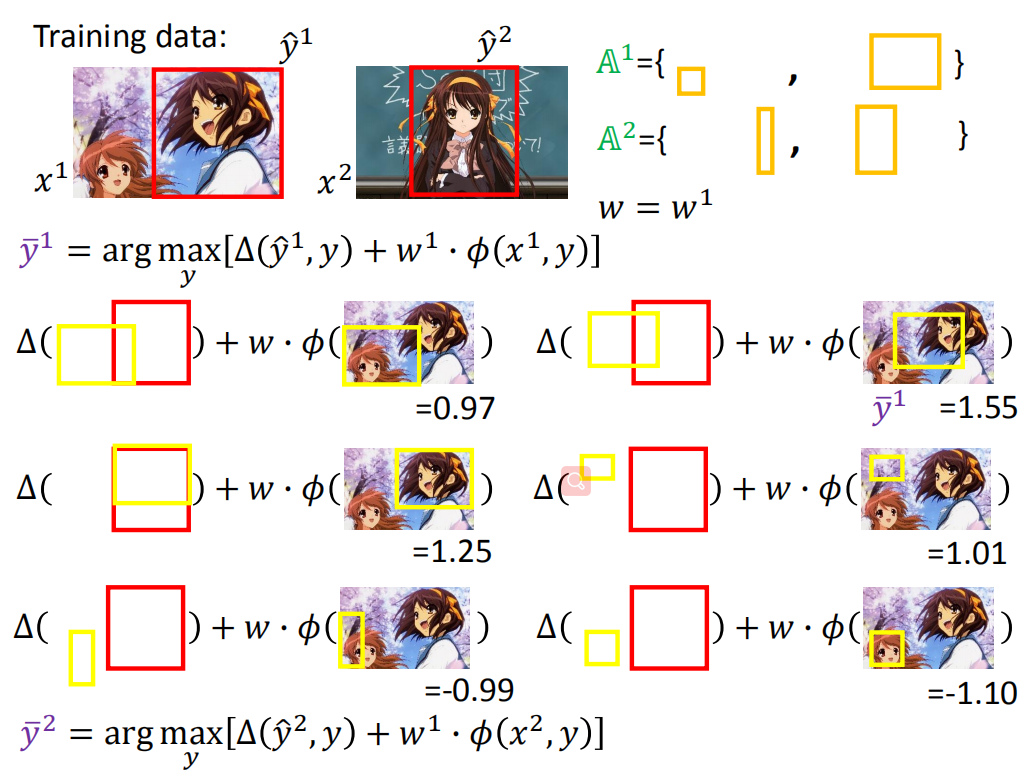
对于第一个training data来说
y
‾
1
=
arg
max
y
[
Δ
(
y
^
1
,
y
)
+
w
1
⋅
ϕ
(
x
1
,
y
)
]
\overline{y}^{1}=\arg \max _{y}\left[\Delta\left(\hat{y}^{1}, y\right)+w^1 \cdot \phi\left(x^{1}, y\right)\right]
y1=argymax[Δ(y^1,y)+w1⋅ϕ(x1,y)]
我们用右上角那个
y
ˉ
1
=
1.55
\bar{y}^1 = 1.55
yˉ1=1.55的黄色框框作为the most violated的约束
当然对第二个training data( ( x 2 , y ^ 2 ) (x^2,\hat{y}^2) (x2,y^2))也做同样的事情,然后更新working set:
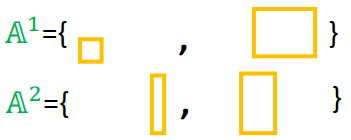
然后用新的working set解决下图QP问题(下图中的working set中有四个约束),计算得到 w = w 2 w = w^2 w=w2
这个过程不断迭代下去,直到 A 1 , A 2 A^1,A^2 A1,A2 不再变化为止。
这里有学生提问,老师又补充了一些知识,在Structured SVM的原版文章中,作者在更新working set上有一个条件,就是在the most violated的约束基础上还要加一个值,满足这个条件的约束才加入working set中,否则不加,这个值越大,整个算法的迭代次数就越少。
Multi-class and binary SVM(多类别与二元支持向量机)
Multi-class SVM(多类别支持向量机)
-
Q1:评估

F ( x , y ) = w ⋅ ϕ ( x , y ) F(x, y)=w \cdot \phi(x, y) F(x,y)=w⋅ϕ(x,y)
如果存在K类,则我们将有K个权值向量:
{ w 1 , w 2 , ⋯ , w K } \left\{w^{1}, w^{2}, \cdots, w^{K}\right\} {w1,w2,⋯,wK}
y的标签自然就有:
y ∈ { 1 , 2 , ⋯ , k , ⋯ , K } y \in\{1,2, \cdots, k, \cdots, K\} y∈{1,2,⋯,k,⋯,K}
从而可以计算得到 w w w和 ϕ ( x , y ) \phi(x,y) ϕ(x,y) :
w = { w 1 w 2 ⋮ w k ⋮ w K } ϕ ( w , y ) = { 0 0 ⋮ x → ⋮ 0 } w = \left\{\begin{matrix} w^1 \\ w^2 \\ \vdots \\ w^k \\ \vdots \\ w^K \end{matrix}\right\} \ \ \phi(w,y) = \left\{\begin{matrix} 0 \\ 0 \\ \vdots \\ \overrightarrow{x} \\ \vdots \\ 0 \end{matrix}\right\} w=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧w1w2⋮wk⋮wK⎭⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎫ ϕ(w,y)=⎩⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎧00⋮x⋮0⎭⎪⎪⎪⎪⎪⎪⎪⎪⎬⎪⎪⎪⎪⎪⎪⎪⎪⎫
w就是权值,主要是 ϕ ( x , y ) \phi(x,y) ϕ(x,y)到底是什么?我们看到 ϕ ( x , y ) \phi(x,y) ϕ(x,y)中只有一个 x → \overrightarrow{x} x,其它都为0,意思就是:当x属于某一个类别时,假设为m,我们就将 x → \overrightarrow{x} x放在 ϕ ( x , y ) \phi(x,y) ϕ(x,y)这个向量的第m个位置上。所以我们的 F ( x , y ) = w ⋅ ϕ ( x , y ) F(x, y)=w \cdot \phi(x, y) F(x,y)=w⋅ϕ(x,y)可以进一步改写为:
F ( x , y ) = w y ⋅ x ⃗ F(x, y)=w^{y} \cdot \vec{x} F(x,y)=wy⋅x -
Q2:推理

F ( x , y ) = w y ⋅ x ⃗ y ^ = arg max y ∈ { 1 , 2 , ⋯ , k , ⋯ , K } F ( x , y ) = arg max y ∈ { 1 , 2 , ⋯ , k , ⋯ , K } w y ⋅ x ⃗ \begin{array}{l}{F(x, y)=w^{y} \cdot \vec{x}} \\ \\ {\hat{y}=\arg \max\limits_{y \in\{1,2, \cdots, k, \cdots, K\}} F(x, y)} \\ {\quad=\arg \max\limits_{y \in\{1,2, \cdots, k, \cdots, K\}} w^{y} \cdot \vec{x}}\end{array} F(x,y)=wy⋅xy^=argy∈{1,2,⋯,k,⋯,K}maxF(x,y)=argy∈{1,2,⋯,k,⋯,K}maxwy⋅x
穷举所有的y,使得F(x, y)最大化,这里类的数量通常很少,所以我们可以穷举它们! -
Q3:训练

- 求得 w , ε 1 , ⋯ , ε N w, \varepsilon^{1}, \cdots, \varepsilon^{N} w,ε1,⋯,εN,最小化C
C = 1 2 ∥ w ∥ 2 + λ ∑ n = 1 N ε n C=\frac{1}{2}\|w\|^{2}+\lambda \sum_{n=1}^{N}\varepsilon^{n} C=21∥w∥2+λn=1∑Nεn
-
对任意的n:
-
对于任意的 ∀ y ≠ y ^ n \forall y \neq \hat{y}^{n} ∀y=y^n:
w ⋅ ( ϕ ( x n , y ^ n ) − ϕ ( x n , y ) ) ≥ Δ ( y ^ n , y ) − ε n , ε n ≥ 0 (1) w \cdot\left(\phi\left(x^{n}, \hat{y}^{n}\right)-\phi\left(x^{n}, y\right)\right) \geq \Delta\left(\hat{y}^{n}, y\right)-\varepsilon^{n}, \varepsilon^{n} \geq 0 \tag{1} w⋅(ϕ(xn,y^n)−ϕ(xn,y))≥Δ(y^n,y)−εn,εn≥0(1)上式中的 Δ ( y ^ n , y ) \Delta(\widehat y^n, y) Δ(y n,y)按之前的说法是指正确分类和错误分类的差距,这个差距是我们可以自己定义的,例如下面:
y ∈ { d o g , c a t , b u s , c a r } Δ ( y ^ n = d o g , y = c a t ) = 1 Δ ( y ^ n = d o g , y = b u s ) = 100 \begin{aligned} & y \in \{dog,cat,bus,car\} \\ & \Delta(\hat{y}^n=dog,y=cat) = 1 \\ & \Delta(\hat{y}^n=dog,y=bus) = 100 \end{aligned} y∈{dog,cat,bus,car}Δ(y^n=dog,y=cat)=1Δ(y^n=dog,y=bus)=100
有N笔训练数据,每一个数据有K个分类,只有一个分类是正确的,那么由K − 1个分类是错误的,所以我们的约束的数量就是:
N ( K − 1 ) N(K-1) N(K−1)
按老师的说法,这些个约束不多,直接算即可。根据前面的定义,我们有:
w ⋅ ϕ ( x n , y ^ n ) = w y ^ ⋅ x ⃗ w ⋅ ϕ ( x n , y ) = w y ⋅ x ⃗ (2) \begin{array}{l}{w \cdot \phi\left(x^{n}, \hat{y}^{n}\right)=w^{\hat{y}} \cdot \vec{x}} \\ {w \cdot \phi\left(x^{n}, y\right)=w^{y} \cdot \vec{x}}\end{array} \tag{2} w⋅ϕ(xn,y^n)=wy^⋅xw⋅ϕ(xn,y)=wy⋅x(2)将(2)代入(1)可以得到;
( w y ^ n − w y ) ⋅ x ⃗ ≥ Δ ( y ^ n , y ) − ε n , ε n ≥ 0 \left(w^{\hat{y}^{n}}-w^{y}\right) \cdot \vec{x} \quad \geq \Delta\left(\hat{y}^{n}, y\right)-\varepsilon^{n}, \varepsilon^{n} \geq 0 (wy^n−wy)⋅x≥Δ(y^n,y)−εn,εn≥0
-
Binary SVM(二元支持向量机)
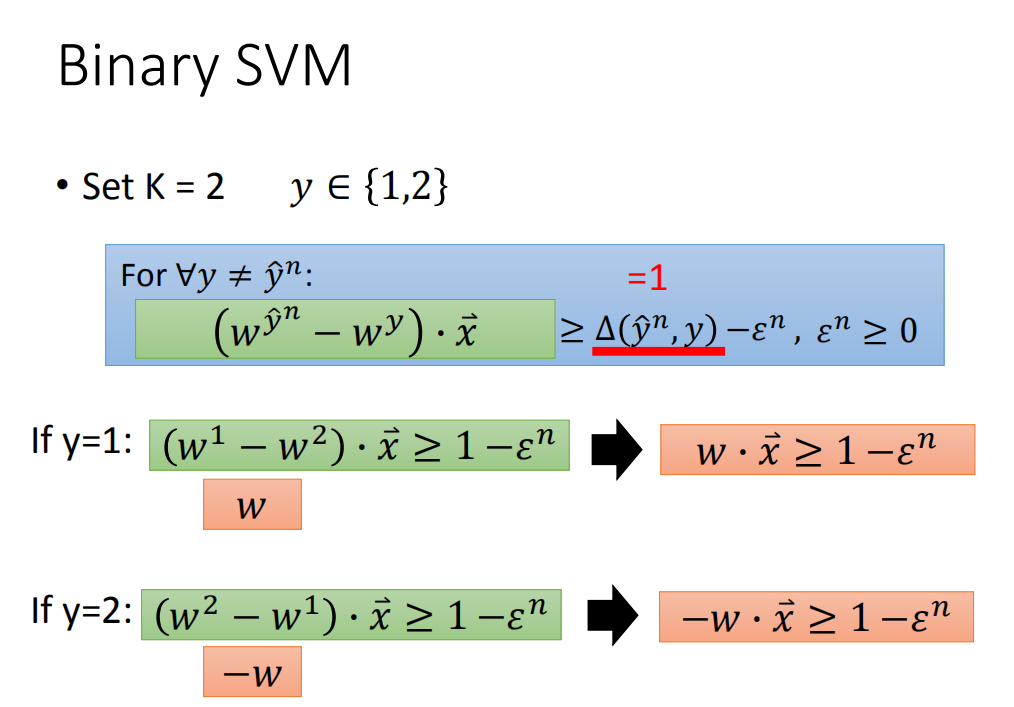
就是多分类中的K=2的场景,这个时候:
y
∈
{
1
,
2
}
y \in \{1,2\}
y∈{1,2}
同样对
∀
y
≠
y
^
n
\forall y \neq \hat{y}^{n}
∀y=y^n:
(
w
y
^
n
−
w
y
)
⋅
x
⃗
≥
Δ
(
y
^
n
,
y
)
−
ε
n
,
ε
n
≥
0
\left(w^{\hat{y}^{n}}-w^{y}\right) \cdot \vec{x} \quad \geq \Delta\left(\hat{y}^{n}, y\right)-\varepsilon^{n}, \varepsilon^{n} \geq 0
(wy^n−wy)⋅x≥Δ(y^n,y)−εn,εn≥0
由于是二分类,我们可以定义当分类不正确的时候:
-
如果y为1:
( w 1 − w 2 ) ⋅ x ⃗ ≥ 1 − ε n \left(w^{1}-w^{2}\right) \cdot \vec{x} \geq 1-\varepsilon^{n} (w1−w2)⋅x≥1−εn令 w 1 − w 2 = w w^1-w^2=w w1−w2=w,可以转换为:
w ⋅ x ⃗ ≥ 1 − ε n w \cdot \vec{x} \geq 1-\varepsilon^{n} w⋅x≥1−εn -
如果y为2:
( w 2 − w 1 ) ⋅ x ⃗ ≥ 1 − ε n \left(w^{2}-w^{1}\right) \cdot \vec{x} \geq 1-\varepsilon^{n} (w2−w1)⋅x≥1−εn
令 w 2 − w 1 = − w w^2-w^1=-w w2−w1=−w,可以转换为:
− w ⋅ x ⃗ ≥ 1 − ε n -w \cdot \vec{x} \geq 1-\varepsilon^{n} −w⋅x≥1−εn
这里就推出了二分类的SVM 的形式,感觉上面的 ϵ n \epsilon^n ϵn 应该对应到相应的上标。
Beyond Structured SVM(open question)(下一步支持向量机(开放问题))
深度神经网络
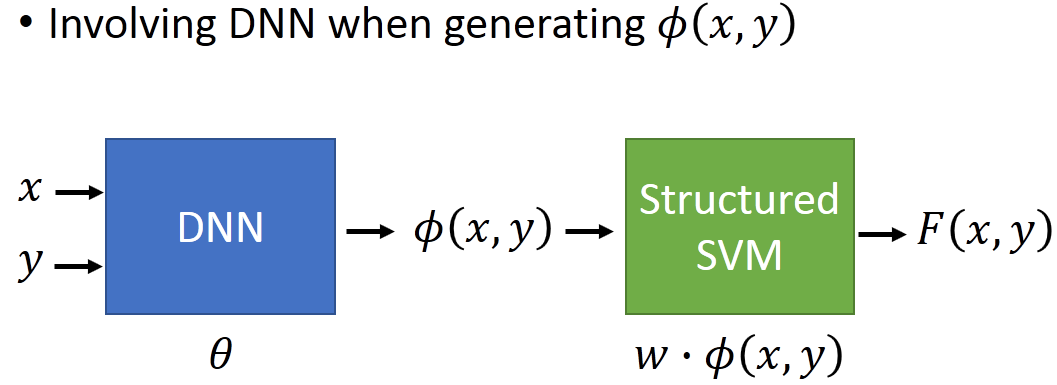
Structured SVM有一个很大的缺陷,就是它是linear的(怪怪的,不是说有一个核的方法来做划分平面,来解决非线性划分方法吗),如果想要结构化SVM的扩展性更好,我们需要定义一个较好的特征,但是人为设定的特征往往十分困难,一个较好的方法是利用DNN生成特征。
先训练好一个DNN来抽取特征,再接一个结构化SVM,最后训练的结果往往十分有效!
Ref:
- Hao Tang, Chao-hong Meng, Lin-shan Lee, “An initial attempt for phoneme recognition using Structured Support Vector Machine (SVM),” ICASSP, 2010
- Shi-Xiong Zhang, Gales, M.J.F., “Structured SVMs for Automatic Speech Recognition,” in Audio, Speech, and Language Processing, IEEE Transactions on, vol.21, no.3, pp.544-555, March 2013
同时训练结构化支持向量机和深度神经网络
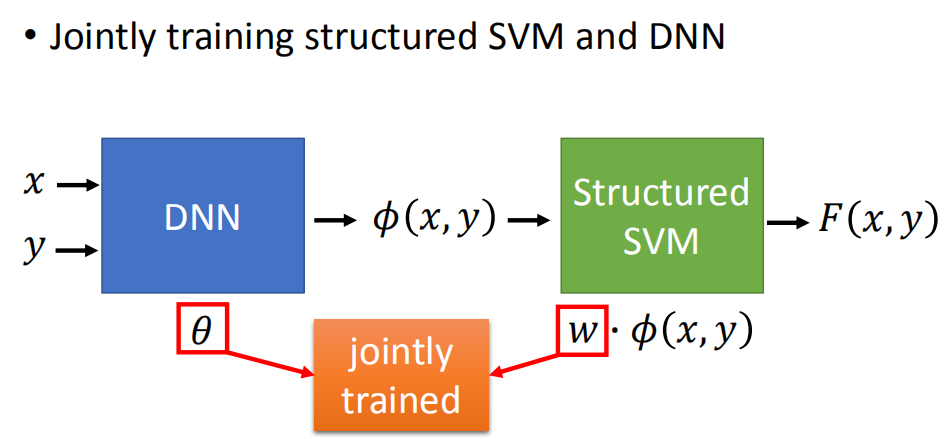
本来是先训练好一个DNN,再接一个结构化SVM。但是可以将DNN与结构化SVM一起训练,同时更新DNN与结构化SVM中的参数!
Ref:
- Shi-Xiong Zhang, Chaojun Liu, Kaisheng Yao, and Yifan Gong, “DEEP NEURAL SUPPORT VECTOR MACHINES FOR SPEECH RECOGNITION”, Interspeech 2015
用深度神经网络代替结构化支持向量机

再用一个DNN代替结构化SVM,即将x和y作为输入,F(x, y)(为一个标量)作为输出!
从而我们的cost就是:
C
=
1
2
∣
∣
θ
∣
∣
2
+
1
2
∣
∣
θ
′
∣
∣
2
+
λ
∑
n
=
1
N
C
n
C = \frac{1}{2}||\theta||^2 + \frac{1}{2}||\theta'||^2 + \lambda \sum_{n=1}^N C^n
C=21∣∣θ∣∣2+21∣∣θ′∣∣2+λn=1∑NCn
其中cost function
c
n
c^n
cn为:
C
n
=
max
y
[
Δ
(
y
^
n
,
y
)
+
F
(
x
n
,
y
)
]
−
F
(
x
n
,
y
^
n
)
C^n = \max\limits_y [\Delta(\hat{y}^n,y)+F(x^n,y)] - F(x^n,\hat{y}^n)
Cn=ymax[Δ(y^n,y)+F(xn,y)]−F(xn,y^n)
Ref:
- Yi-Hsiu Liao, Hung-yi Lee, Lin-shan Lee, “Towards Structured Deep Neural Network for Automatic Speech Recognition”, ASRU, 2015






















 1981
1981











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








