sk09.【scikit-learn基础】--『无监督学习』之K均值聚类

最新推荐文章于 2025-10-15 20:08:11 发布

派森先生

最新推荐文章于 2025-10-15 20:08:11 发布

阅读量1k

点赞数 25

CC 4.0 BY-SA版权

分类专栏： scikit-learn 文章标签： scikit-learn 学习均值算法

本文链接：https://blog.csdn.net/qq_44846224/article/details/153329971

scikit-learn 专栏收录该内容

16 篇文章

订阅专栏

聚类是机器学习中常见的一类问题，它通过样本的近似度将样本聚为一定的类别。本文先介绍聚类问题是什么，聚类的意义，然后通过层次聚类来讲解聚类算法是什么。通过本文，可以初步认识什么是聚类，什么是聚类算法，以及聚类的难点

1. 什么是聚类问题

聚类是针对给定的样本，依据样本特征的相似度或距离，将其归并到若干个“类”或“簇”的算法。聚类的目的是通过得到的类或簇来发现数据的特点，在数据挖掘、模式识别等领域有着广泛的应用。区别于监督学习的“特征+标签”的样本模式，聚类的样本只有“特征”，事先并不知道样本的标签（类或簇）。

2.聚类的意义

聚类是非常有意义的，下面我们通过两个场景说明聚类问题的意义

聚类问题应用于-降维分析

例如，我们采集了150组发烧病人样本，如果把发烧病人的症状用聚类方法打上类别标签，最后确定为5个类别，那么我们分析问题就不需要对150个样本分析，而是降维后的5个类别进行分析

聚类问题应用于-按类别服务

我们对已有客户进行聚类，聚成k类如果来了新客户，那我们判断他属于哪一个类别，就能针对性提供服务了。例如音乐推荐，先把已有用户聚类，来了新用户，就把和他同一类别的用户喜欢的音乐推荐给他

03.聚类与层次聚类

聚类问题一个较理想的解决方案是“层次聚类算法”，
层次聚类算法的聚类流程如下：

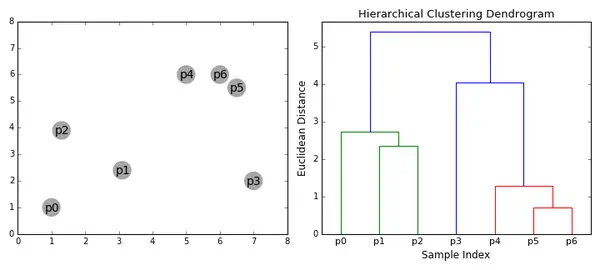
层次聚类算法先把所有样本都当成一个类别，每次把最近的两个类别聚合为一个类别(每次减少一个类别)。当类别的距离都比较大，或者类别个数足够小时，就停止聚类。从层次聚类算法的过程可以感受到，层次聚类算法非常有聚类的感觉。

提醒

层次聚类算法是一种较为理想、朴素的聚类方法，但它最大缺点是计算量非常大，这是因为每次合并前都要计算所有类别两两间的距离，当样本量较大时，计算量就极极极大。
例如10万个样本，那样本两两间的距离就有100亿，这样的计算量几乎无法完成。因此，层次聚类在样本较少时可以使用，但大部分实际情况并不适合使用层次聚类。聚类问题有很多解决方法，但计算量过大往往都是这些聚类方法的通病。而k-means则是一种计算量较小，不会因为数据量暴增而暴增的方法。由于k-means效果不错，且具可行性，因此k-means是日常用得最多的基础入门聚类算法。

04.K-means聚类流程

k-means聚类算法流程如下：

1. 初始化K个聚类中心
2. 将每个样本划分到离它最近的聚类中心
         这里需要先计算各个样本与聚类中心的距离，再进行划分
3. 将每个聚类中心更新为样本质心

        将所有属于第i个聚类中心的样本的均值，作为第k个聚类中心的位置
4. 重复2、3，直到达到终止条件
         终止条件为：达到最大迭代次数或聚类中心变化很小

05.K-means的关键参数

1、K值的选择
          根据数据背景意义来推断样本大概有多少个类别，从而确定聚类中心个数K, 在不太明确的时候，可以设置5类左右，对数据进行预试探。为什么设5类呢？因为如果真实类别小于5类，那后期合并即可，如果多于5类，那至少也能先聚出几个类别，后面再增加即可。
2、聚类中心的初始化
         常用的方法是随机选取k个样本作为聚类中心
  三、距离公式
          最常用的距离公式就是欧氏距离，余弦距离，曼哈顿距离
欧氏距离的计算公式如下：
                         $\mathbf{d}(x, y) = \sum_{i=1}^{n} \sqrt{(x_i - y_i)^2} = \sqrt{(x_1 - y_1)^2 + (x_2 - y_2)^2 + \cdots + (x_n - y_n)^2}$

余弦距离的计算公式如下：

$\mathbf{d}(x, y) = \cos \langle x, y \rangle = \frac{x \cdot y}{\|x\| \cdot \|y\|}$

曼哈顿距离计算公式如下：
$\mathbf{d}(x, y) = \sum_{i=1}^{n} |x_i - y_i| = |x_1 - y_1| + |x_2 - y_2| + \cdots + |x_n - y_n|$

还有一大堆距离，例如切比雪夫距离、闵可夫斯基距离、马氏距离等等，日常中基本用欧氏距离，一般欧氏距离效果不好再考虑其它距离。

注意的是

1.  K-means对初始化比较敏感，需多次尝试
         kmeans非常受初始化的影响，因此，一般采用随机初始化。然后多次聚类并用SSE进行评估，哪个结果好，就用哪个
2. 类别个数需要多次尝试
         kmeans 对 K值也是敏感的，也需要多次尝试

聚类结果评估函数-误差平方和 (SSE)

$\text{SSE} = \sum_{i=1}^{m} (x_i - C_{x_i})^2$

$C_{x_i}$ ： xi所属的聚类中心

06.K-means代码实现与优缺点

import matplotlib.pyplot as plt
from sklearn.datasets import make_blobs
from sklearn import cluster

# -----------生成数据-----------------
X, y = make_blobs(n_samples=150, random_state=10,centers=5)           #生成数据

# ---------模型训练与预测-------------
clf = cluster.KMeans(n_clusters=5, max_iter=300,random_state=0)       # 初始化k-means聚类模型
clf.fit(X)                                                            # 进行聚类
y = clf.predict(X)                                                    # 输出每个样本的类别

# --------------打印结果---------------
print('\n聚类中心:\n',clf.cluster_centers_)                           # 打印聚类中心
#展示结果，以颜色标示类别    
fig, axes = plt.subplots(2, 1,figsize=(8, 6))                         # 初始化画布
plt.subplots_adjust(wspace=0.2, hspace=0.3)                           # 调整子图之间的间隔 
plt.rcParams["font.sans-serif"] = ["SimHei"]                          # 设置中文
plt.rcParams['axes.unicode_minus'] = False                            # 设置坐标轴负号显示方式 
axes[0].set_title('原始样本')                                         # 设置第一个子图的标题
axes[0].scatter(X[:, 0], X[:, 1])                                     # 画出聚类前的样本分布
axes[1].set_title('k-means 聚类结果')                                 # 设置第一个子图的标题
axes[1].scatter(X[:, 0], X[:, 1], c=y)                                # 画出聚类后的各个样本的类别

运行结果如下：

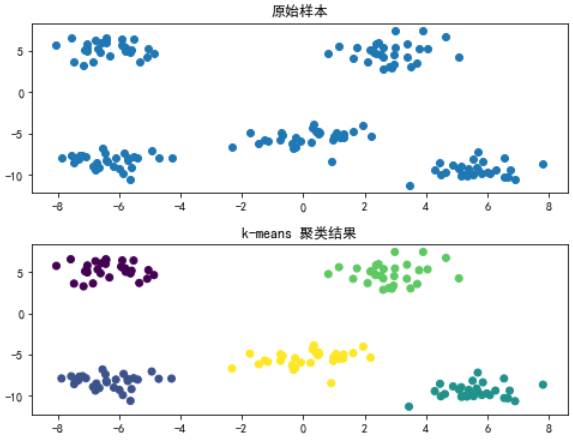
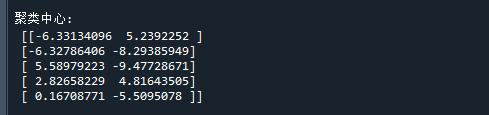
K-means的优缺点

优点
         K-means的优点是计算量低，相比其它聚类算法，不会因为样本量而暴增
         K-means每次只需计算样本与类别的距离，而不是样本与样本间的距离,类别个数是很小的，所以 k-means相对于其它聚类算法计算量不大
缺点
1. K值需要先验经验去决定
          k值需要用先验经验决定，而往往这恰好是缺失的, 如果k值设置得不好，会严重影响聚类结果
  2. 对异常点较敏感
         k-means对异常点较为敏感，异常点极大时会严重影响聚类中心的位置
  3. 对球状的数据比较好用
         对球状的数据比较好用，但在数据为非球状数据时，效果可能会不佳

K-means最最最大的优点就是计算较为简单
聚类的方法千千万种，但K-means经典不衰就是因为它的计算量在众多聚类算法中是最简单的