机器学习小白：高斯判别分析（GDA）

好文链接：
https://www.cnblogs.com/jcchen1987/p/4424436.html

https://blog.csdn.net/xiaolewennofollow/article/details/46406447?utm_medium=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase&depth_1-utm_source=distribute.pc_relevant_t0.none-task-blog-BlogCommendFromMachineLearnPai2-1.nonecase

假设已有数据：

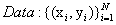
目标函数：

其中 y 符合伯努利分布：注意两类样本的分布 均值不同，方差相同

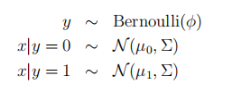
应该是个漂亮小姐姐的笔记：
由上一张图可以看出，当y=1和0时概率不同，写在一起后为

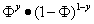
记住这个式子，之后会用于公式的推导.

通过对数极大似然估计（也是偷小姐姐的图，自己的字太丑，haha），函数为样本发生的概率取对数；接下来就是让函数L最大化，要对四个参数求导数

求导过程直接省略，看了你也记不住，只记最后结论为：
（1）

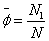
N为样本总数，N1为第一类样本数量，N2为第二类样本数量
（2）

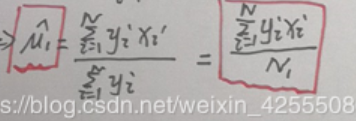
（3）u2的估计只需要将上式中 yi 换成（1-yi）;N1换成N2

（4）

总结：

import matplotlib.pyplot as plt
from numpy import *


mean0=[2,3]
cov=mat([[1,0],[0,2]])
x0=random.multivariate_normal(mean0,cov,500).T   #label 为 0，这也是高斯判别分析公式推导时的条件
y0=zeros(shape(x0)[1])

# x0.shape                                       #2行500列，每一列是一个数据，第一类有500个二维样本
mean1=[7,8]
cov=mat([[1,0],[0,2]])
x1=random.multivariate_normal(mean1,cov,300).T
y1=ones(shape(x1)[1])                            #第二类样本label 是1


x=array([concatenate((x0[0],x1[0])),concatenate((x0[1],x1[1]))])#将两中样本数据拼接
y=array([concatenate((y0,y1))])

m=shape(x)[1]                                   # m是样本的列数，这里也是样本的总数


# #计算参数:\phi,\u0,\u1,\Sigma
phi=(1.0/m)*len(y1)                             # phi 为0.375， label=1的样本数占总样本数

u0=mean(x0,axis=1)                              #[2.03983572 3.10866202],第一类样本两个维度的均值
u1=mean(x1,axis=1)                              #[7.07794924 8.00548557],第二类样本两个维度的均值

#下面是最难求的Σ
xplot0=x0;xplot1=x1   #save the original data  to plot 
x0=x0.T;x1=x1.T;x=x.T                           #将数据转置，方便相乘

x0_sub_u0=x0-u0
x1_sub_u1=x1-u1
x_sub_u=concatenate([x0_sub_u0,x1_sub_u1])


x_sub_u=mat(x_sub_u)                           #使用mat函数 之后才能使用一些线性代数的操作


sigma=(1.0/m)*(x_sub_u.T*x_sub_u)              #最后求出Σ是个2×2的矩阵，符合理论，因为每个样本只有两个维度
sigma.shape              

# #画出决策边界 
midPoint=[(u0[0]+u1[0])/2.0,(u0[1]+u1[1])/2.0]
#print midPoint
k=(u1[1]-u0[1])/(u1[0]-u0[0])                 #决策边界的斜率的倒数，为什么是这个代码之后会讲
#print k
x=range(-2,11) 
y=[(-1.0/k)*(i-midPoint[0])+midPoint[1] for i in x]#斜率有了，但是只有斜率只不过是一条过原点的直线罢了
                                                   #截距为依旧很重要，截距计算的是y轴这个维度两类样本的均值，有了k和b 之后决策边界就可以画出来了



    
##这下面都是画图像了，不必深究
# #plot contour for two gaussian distributions
# def gaussian_2d(x, y, x0, y0, sigmaMatrix):
#     return exp(-0.5*((x-x0)**2+0.5*(y-y0)**2))
# delta = 0.025
# xgrid0=arange(-2, 6, delta)
# ygrid0=arange(-2, 6, delta)
# xgrid1=arange(3,11,delta)
# ygrid1=arange(3,11,delta)
# X0,Y0=meshgrid(xgrid0, ygrid0)   #generate the grid
# X1,Y1=meshgrid(xgrid1,ygrid1)
# Z0=gaussian_2d(X0,Y0,2,3,cov)
# Z1=gaussian_2d(X1,Y1,7,8,cov)

# #plot the figure and add comments
# plt.figure(1)
# plt.clf()
# plt.plot(xplot0[0],xplot0[1],'ko')
# plt.plot(xplot1[0],xplot1[1],'gs')
# plt.plot(u0[0],u0[1],'rx',markersize=20)
# plt.plot(u1[0],u1[1],'y*',markersize=20)
# plt.plot(x,y)
# CS0=plt.contour(X0, Y0, Z0)
# plt.clabel(CS0, inline=1, fontsize=10)
# CS1=plt.contour(X1,Y1,Z1)
# plt.clabel(CS1, inline=1, fontsize=10)
# plt.title("Gaussian discriminat analysis")
# plt.xlabel('Feature Dimension (0)')
# plt.ylabel('Feature Dimension (1)')
# plt.show(1)

接下来我们将看一下决策边界的斜率是怎么求出来的

图中与决策边界垂直的线的斜率可以轻松看出为
(u1[1]-u0[1])/(u1[0]-u0[0]) ，而两线垂直，斜率之积为-1，从而可以轻易得出决策边界的斜率