4. 分类_对于一个四分类问题,模型的预测结果以及真实标签如下所示:预测值:1 2 3 4 1 3-CSDN博客

本文链接：https://blog.csdn.net/qq_45276194/article/details/130206048

将线性回归应用于分类问题不是一个很好的选择，如果“运气好”会得到好的预测运气不好就是不好的结果或者说很差的预测。

Logistic Regression（一种分类算法）可以将 $h_{\theta}(x)$ 的输出值控制在[0, 1]之间。

4.1 假设表示

我们希望我们分类器的输出值控制在[0, 1]之间，所以我们提供了一个假设来满足该性质。

当我们运用线性回归时，我们用的假设形式是： $h_{\theta}(x) = \theta^{T}x$

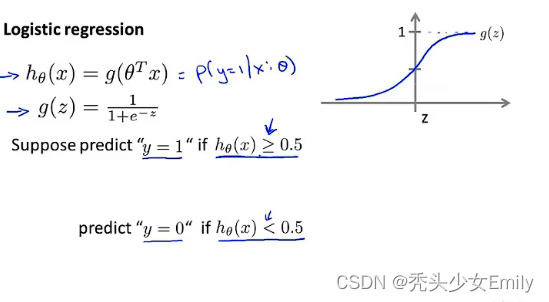
对于logistic regression，我们的假设形式是： $h_{\theta} (x)= g(\theta^{T}x)$ （logistic函数），而 $g(z) = \frac{1}{1 + e^{-z}}$ （sigmoid函数），logistic函数和sigmoid函数其实本质上没差别，可以随意选择哪个名词代表g，结合两者我们可以得到： $h_{\theta} = \frac{1}{1 + e^{-\theta^{T}x}}$

sigmoid函数图像如下：

解释假设 $h_{\theta}(x)$ 的输出：当假说 $h_{\theta}(x)$ 输出某个数字，我们会把这个数字当作对一个输入x和y=1的概率估计。

例子：比如我们使用肿瘤分类的例子，因此我们可能有一个特征向量x，同往常 $x_{0} = 1$ 一样、然后我们有一个特征是肿瘤的大小。假设有一个病人来了，他的肿瘤是某个大小，把他的特征向量x作为我们的假设 $h_{\theta}(x)$ 中，并假设我们的假设输出是0.7。这个假设输出告诉我们，对于一个特征为x的患者和y=1的概率是0.7。换句话说，需要告诉患者这个肿瘤有70%或者0.7的可能性是恶性肿瘤。

用公式写的话就是： $h_{\theta}(x) = P(y=1|x;\theta)$

而且： $P(y=0|x;\theta) + P(y=1|x;\theta) = 1$

4.2 决策边界

假设我们有一个训练集

假设我们的假设函数是： $h_{\theta}(x) = g(\theta_{0} + \theta_{1}x_{1} +\theta_{2}x_{2} )$

在这里，假设我们的拟合值为： $\theta_{0} = -3,\theta_{1} = 1,\theta_{2} = 1$

在训练集图上的那条洋红色的线，就被称作决策边界。

再看一个更复杂的训练集

怎么样才能用logisitic函数来拟合呢？

假设我们的假设函数是： $h_{\theta}(x) = g(\theta_{0} + \theta_{1}x_{1} +\theta_{2}x_{2} + \theta_{3}x_{1}^{2} + \theta_{4}x_{2}^{2} )$

假设我们的拟合值为： $\theta_{0} = -1,\theta_{1} = 0,\theta_{2} = 0,\theta_{3} = 1,\theta_{4} = 1$

4.3 拟合logistic回归

用来拟合参数的优化目标或者叫代价函数

下图是监督学习问题中的logistic回归模型的拟合问题

在线性回归中我们的代价函数是： $J(\theta) =\frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}(h_{\theta }(x^{(i)}) - y^{(i)})^{2}$

而在这里，我们把后面的平方项换成： $Cost(h_{\theta}(x^{(i)}), y^{(i)}) =\frac{1}{2}(h_{\theta }(x^{(i)}) - y^{(i)})^{2}$

在这里有个问题，它呈现出来的图像是非凸函数，这使得梯度下降很难找到收敛值。

因此我们找到了一个新的代价函数用在logistic回归上：

$Cost(h_{\theta}(x), y) = \left\{\begin{matrix} -log(h_\theta(x)), if y =1 \\ -log(1-h_\theta(x)) ,if y =0 \end{matrix}\right.$

如果y=1的情况：

$Cost = 0 ,if y=1,h_{\theta}(x)=1$

$h_{\theta}(x)\rightarrow 0$ , $Cost\rightarrow \infty$

就相当于，我们的假设函数说y=1的概率等于0，相当于对病人说你患恶性肿瘤的概率为0，但如果病人的肿瘤确实是恶性的，即如果y最终等于1，即使我们告诉病人它发生的概率为0，但结果是这个预测是错的。这样的情况，预测的代价就是无穷的（也就是代价很大，完全预测错了）

如果y=0的情况：

总结：代价函数表示了预测值与实际值的差距，规避取不到全局最优的问题。

4.4 简化代价函数和梯度下降

这一小节会找出一种稍微简单一点的方法来写代价函数来替换我们现在用的方法，同时我们还要弄清楚如何运用梯度下降法来拟合logistic回归的参数。

我们整体的代价函数是：

$J(\theta) =\frac{1}{m}\sum_{i=1}^{m}\frac{1}{2}(h_{\theta }(x^{(i)}) - y^{(i)})^{2}=\frac{1}{m}Cost(h_{\theta}(x^{(i)}), y^{(i)})$

$Cost(h_{\theta}(x), y) = \left\{\begin{matrix} -log(h_\theta(x)), if y =1 \\ -log(1-h_\theta(x)) ,if y =0 \end{matrix}\right.$

Note:在我们的训练集中，关于分类问题的y的值总是等于0或1

可以将 $Cost(h_{\theta}(x), y)$ 改写成： $Cost(h_{\theta}(x), y) = -ylog(h_{\theta}(x)) - (1-y)log(1-h_{\theta}(x))$

所以，logistic回归的代价函数如下：

$J(\theta) =\frac{1}{m}Cost(h_{\theta}(x^{(i)}), y^{(i)})=-\frac{1}{m}[\sum_{i=1}^{m}y^{(i)}log(h_{\theta}(x^{(i)})) + (1-y^{(i)})log(1-h_{\theta}(x^{(i)}))]$

根据这个代价函数，为了拟合出参数，我们要做的是：找出让 $J(\theta)$ 取得最小值的参数 $\theta$ ， $\underset{\theta}{min}J(\theta)$

由于 $\frac{\partial }{\partial \theta_{j}}J(\theta) = \frac{1}{m}\sum_{i=1}^{m}(h_{\theta(x^{(i)})}-y^{(i)})x_{j}^{(i)}$

repeat的部分又可以替换成下图所示

会惊讶的发现和线性回归的梯度下降一样！（但其实在线性回归里面 $h_{\theta}(x) = \theta^{T}x$ ，而这里的 $h_{\theta}(x) = \frac{1}{1+e^{-\theta^{T}}x}$ ）

在前面讲过的特征缩放在这里也适用

4.5 高级优化算法

共轭梯度法（Conjugate Gradient）、BFGS和L-BFGS就是优化之前的梯度算法的一些更高级的算法。

使用上述三种算法中的任意一种，通常不需要手动选择学习率 $\alpha$ ，并且收敛得远远快于梯度下降。

缺点就是笔比梯度下降复杂得多，现阶段能使用就行，理解恐怕要话很久的时间。

使用这些算法的例子：

怎样运用到logistic回归中呢？

4.6 多元分类-一对多

什么是多类别分类问题？

例子：假如说你现在需要一个学习算法，自动的将邮件归类到不同的文件夹里或者说可以自动地加上标签，你有一些不同的文件夹或者不同的标签来区分比如说：工作的、朋友的、家人的或者是有关兴趣爱好的邮件。我们就有了一个包含四个分类的问题，用y=1，y=2，y=3，y=4来代表Work,Friends,Family,Hobby。这就是多类别分类问题