概率论——7 常见概率分布及其分布率

0-1分布

定义

设随机变量$X$只可能取0和1两个值，它的分布律是
P { X = k } = p k ( 1 − p ) 1 − k , k = 0 , 1 ( 0 < p < 1 ) P\left\{X=k\right\}=p^k(1-p)^{1-k},k=0,1(0<p<1) P{X=k}=pk(1−p)1−k,k=0,1(0<p<1)
则称$X$服从参数为$p$的(0-1分布)或两点分布。

表格形式如下：

应用

1. 在事件仅有两个样本点时可以用0-1分布来刻画。

2. 在有多个样本点时，可以构造某事件发生而其他事件不发生或者某个事件不发生其他事件发生，来构造出0-1分布进行简化。如：

   

二项分布

伯努利试验

设试验$E$只有两个可能结果：$A$及$\bar{A}$，则称$E$为伯努利试验。设$P(A)=p(0<p<1)$

将$E$独立重复地进行$n$次，则称这一串重复的独立试验为$n$​重伯努利试验

注：”重复“是指在每次试验中$P(A)=p$保持不变；“独立”是指各次试验的结果互不影响

定义

若$X$的分布律为：

P { X = k } = C n k p k ( 1 − p ) n − k , k = 0 , 1 , 2 , . . . , n P\{X=k\}=C_n^kp^k(1-p)^{n-k},k=0,1,2,...,n P{X=k}=Cnk​pk(1−p)n−k,k=0,1,2,...,n

则称$X$服从参数为$n,p$的二项分布，记为$X\sim b(n,p)$

当$n=1$时，二项分布就是0-1分布

二项分布的概率规律

当$k$增加时， P { X = k } P\{X=k\} P{X=k}先单调增加，达到最大值后，随后单调减少：

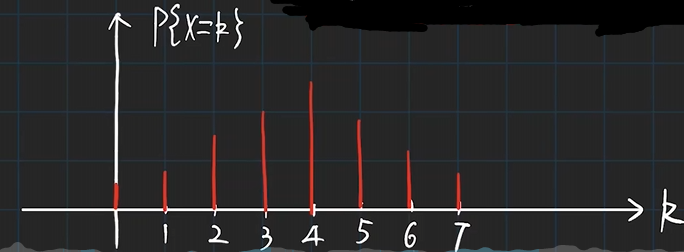
例子

• 抽检产品质量
• 射击试验
• …

泊松分布

当二项分布中的$n\to \infty$时，$X$应该服从什么样的分布？

定义

若随机变量$X$的分布律为：

P { X = k } = λ k e − λ k ! , k = 0 , 1 , 2 , . . . P\{X=k\}=\frac {λ^ke^{-λ}} {k!},k=0,1,2,... P{X=k}=k!λke−λ​,k=0,1,2,...

其中$\lambda >0$是常数，则称随机变量$X$服从参数为$\lambda$的泊松分布，记为$X\sim P(\lambda )$

实际上在高等数学的级数中有这样的结论：

${\sum }_{n=0}^{\infty }\frac{x^n}{n!}=e^x$

所以易证明：

${\sum }_{k=0}^{\infty }\frac{{\lambda }^k{e}^{-\lambda }}{k!}=1$

泊松定理

泊松定理有以下两个应用：

1. 泊松定理说明了当$n\to \infty$时，二项分布的极限就是泊松分布
2. 当$n$很大（$n\ge 20$），$p$很小（$p\le 0.05$）时，有二项分布近似公式：

P { X = k } = C n k p k ( 1 − p ) n − k ≈ λ k e − λ k ! , λ = n p P\{X=k\}=C_n^kp^k(1-p)^{n-k}\approx\frac {λ^ke^{-λ}} {k!},λ=np P{X=k}=Cnk​pk(1−p)n−k≈k!λke−λ​,λ=np

几何分布

定义

在独立重复试验中，试验次数预先不能确定。设每次试验成功的概率为$p$，将实验进行到成功一次为止，以$X$表示所需的试验次数，则$X$的分布律为：
P { X = k } = ( 1 − p ) k − 1 p , k = 1 , 2 , . . . P\{X=k\}=(1-p)^{k-1}p,k=1,2,... P{X=k}=(1−p)k−1p,k=1,2,...
则称随机变量$X$服从参数为$p$的几何分布。

几何分布的分布律应该是一个公比为$k$的等比数列。

超几何分布

定义