DCT变换

黑曼巴、。；

已于 2024-11-05 20:20:38 修改

阅读量1.1k

点赞数 11

文章标签：图像处理

于 2024-06-15 18:51:25 首次发布

本文链接：https://blog.csdn.net/qq_45607390/article/details/139706632

版权

文章目录

灰度图测试

由于DCT只能对单通道数据进行，所以先介绍灰度图。

图像有RGB表示和**YCbCr（亮度、色度Chroma）**表示等。

利用matlab的rgb2gray函数可以将3通道彩色图转换为灰度图

得到图像灰度图还有另一种方式，就是用matlab的rgb2ycbcr函数转换为YCbCr颜色表示，然后单独将Y通道提取出来显示就是灰度图。

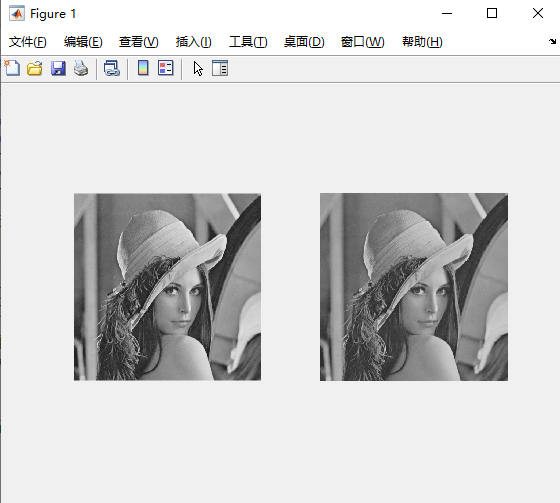
经过试验，得到的图像视觉上没有明显差异，但灰度图数值不同。

%% 读取图像
clc;clear;close all;
img = imread("image\lena.png");
img_gray = rgb2gray(img);
img_ycbcr = rgb2ycbcr(img);
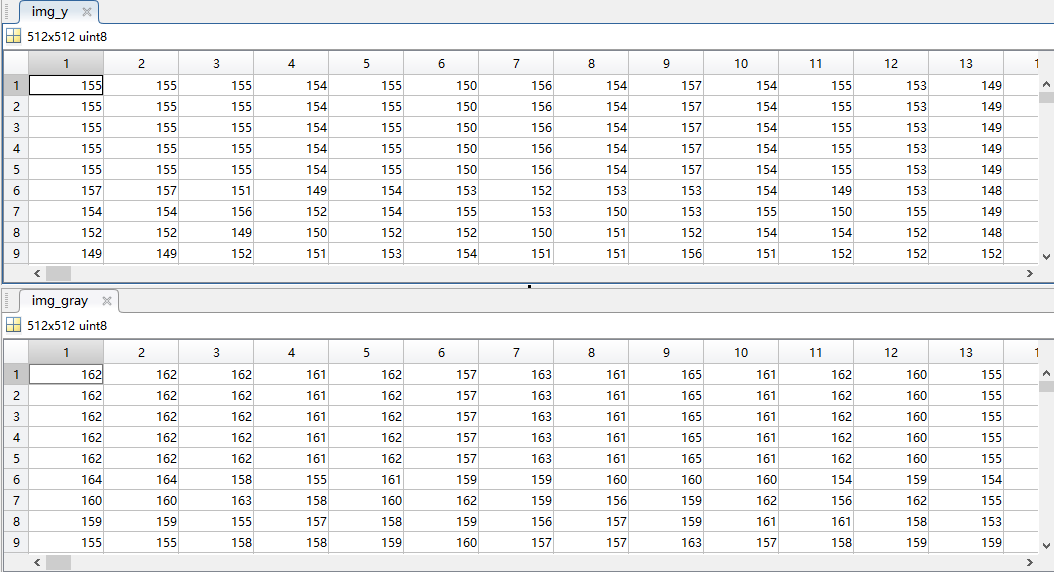
img_y = img_ycbcr(:,:,1);

%% 看是否灰度图和YCbCr的Y分量相不相同
subplot(1,2,1);
imshow(img_gray);
subplot(1,2,2);
imshow(img_ycbcr(:,:,1)); % 视觉效果没有明显差异，但是数值不一样

图像的高频与低频

图像不仅可以看做是像素点的组合，还可以从信号的角度来看，我们可以将图像的任意一行取出来绘制折线图：

%% 画256行的一个折线图
img_row = img_gray(256,:);
figure;
plot(img_row);

%% 在三维空间绘制像素变化情况
[height, width] = size(img_gray);
[X, Y] = meshgrid(1:width, 1:height);
Z = double(img_gray);
figure;
surf(X, Y, Z);
colormap('jet');
colorbar;
view(3);
axis equal;
grid on;
shading interp;
xlabel('X');
ylabel('Y');
zlabel('Pixel Value');
title('Image as a Smooth Surface');

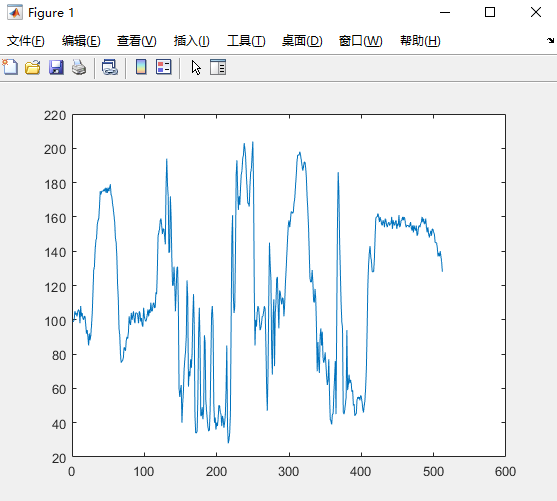
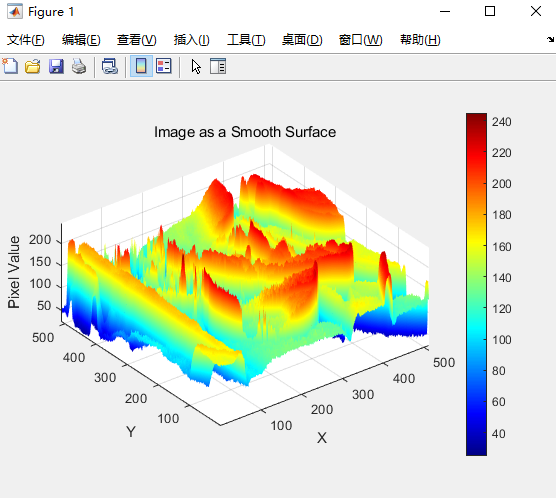
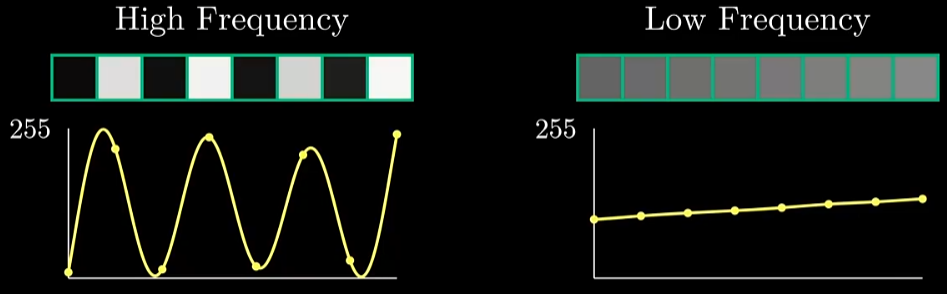
可以看到整个像素行有变化剧烈的部分以及变化平缓的部分。

实际上图像的低频信号就是像素变化平缓的部分，而像素的高频信号就是像素变化剧烈的部分，也常常有高频噪声的说法。而人眼对于高频细节信号是不敏感的。对于低频信号较为敏感。

需要注意的一点是，现实世界中由相机拍摄的图像一般在像素间由较强的相关性，也就是一个小区域内的像素值一般比较接近，所以应该由大量的低频信号组成，而高频信号只占一小部分。

那么图像的高频和低频，甚至于是不同频率的信号如何进行提取，这就需要用到DCT变换（Discrete Cosine Transform），通过DCT变换与逆DCT变换，可以将一幅图像的像素值用不同频率余弦分量的线性组合表示。

DCT变换现象观察

理论上，DCT变换可以应用于任意长度的输入，但简单起见，只考虑8个样本点：

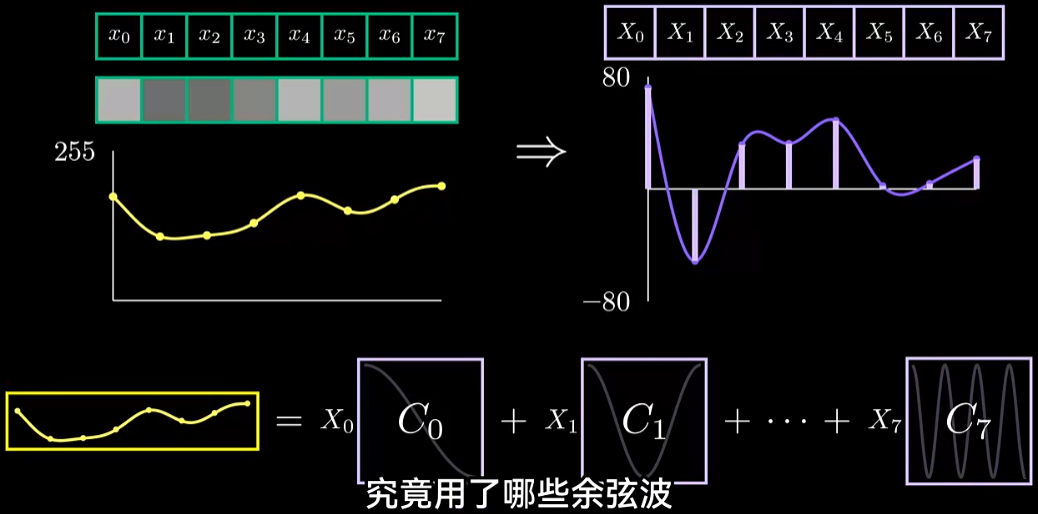
考虑8个样本点 $x_0,x_1,..x_7$ ，经过DCT变换后得到一个等长的系数向量 $X_0,X_1,...,X_7$ ，这就是离散余弦变换的目的：得到原始信号中由哪些余弦波组成，以及组成系数是多少。这里的 $C_0,C_1,...C_7$ 就是不同频率的余弦波。

为了直观地看到当原始信号变化时，得到的DCT变换系数如何变化，我们不妨考虑输入一个标准余弦函数：

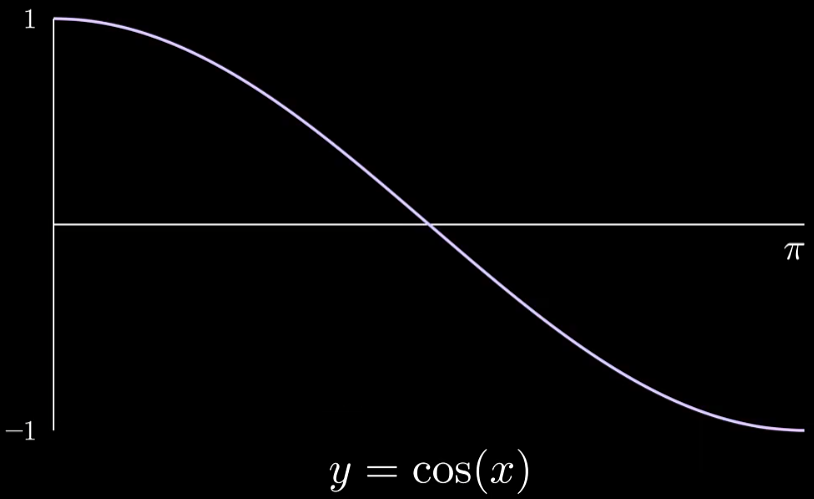
由于余弦函数是连续的，要应用DCT，我们首先需要对其进行采样，也就是在 $[0,\pi]$ 内采样8个样本点，这里用如下的采样方法：将 $[0,\pi]$ 区间分成8等份，然后以每个子区间的中点位置为一个样本点（实际上这样采样和DCT变换中的余弦波保持了一致）：

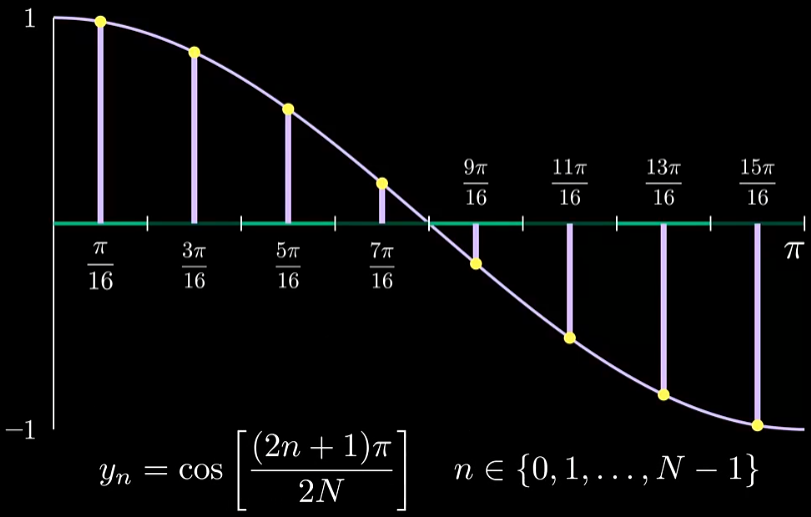
现在只考虑 $N = 8$ 的情况，其他情况可以类似地推广。

现在我们可以将采样得到的样本点向量输入DCT变换了，我们将观察到原始信号在以下三种情况下，DCT系数的变化情况：

振幅变化
上下平移
频率变化

振幅变化

%% 振幅变化时 DCT的变化情况：DCT对应分量也变化，如果反向，DCT图像也会跟着反向
figure;
for k = [-1,1,2]
    for i = 0:7
        y(i+1) = k * cos((2*i+1)*pi / 16); %对标准余弦函数cos(x)进行采样，[0,π]采样8个点
    end
    y_dct = dct(y);
    plot(y_dct);
    hold on;
end
title("余弦函数振幅变化时，其DCT的变化情况")
legend("取负","振幅为1","振幅为2");

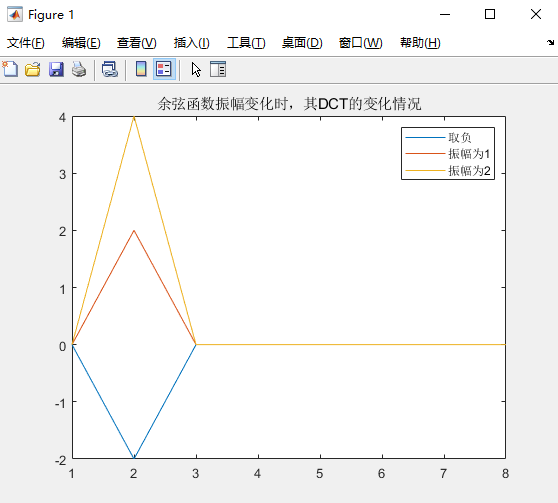
可以看到，当振幅变化时，DCT系数对应的第2个分量 $X_1$ 的值也发生了变化，而其他分量都是0。

上下平移

%% 上下平移时，DCT的变化情况
figure;
for b = [-1,1]
    for i = 0:7
        y(i+1) = cos((2*i+1)*pi / 16) + b;
    end
    y_dct = dct(y);
    plot(y_dct);
    hold on;
end
title("余弦函数上下平移时，其DCT的变化情况")
legend("向下平移1","向上平移1");

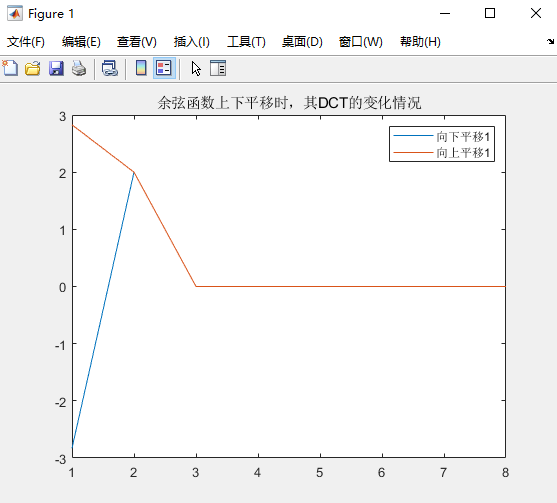
当原始余弦信号上下平移时，可以看到第二个DCT系数的峰值依然存在并保持不变，而上下平移只改变了第一个DCT系数 $X_0$ 的值（后面将得到第一个系数实际上直流分量，其他系数是交流分量），除前两个系数外，其他DCT系数都是0。

频率变化

%% 频率变化时，DCT的变化情况
figure;
for k = 1:3
    for i = 0:7
        y(i+1) = cos((2*i+1)*pi*k / 16);
    end
    y_dct = dct(y);
    subplot(1,3,k);
    plot(y_dct);
    title(strcat("频率系数为", num2str(k)));
end
sgtitle("余弦函数频率变化时，DCT的变化情况");

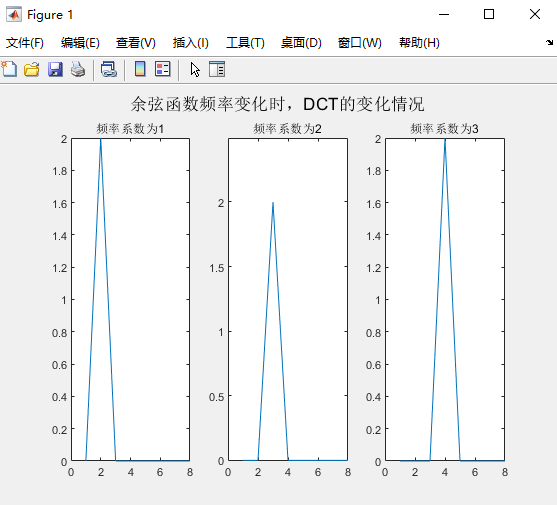
当原始余弦信号频率发生变化时，可以看到DCT系数峰值的位置也发生了变化，频率与其峰值的 $x$ 索引是一一对应的。可以以此类推，频率系数为4时，峰值对应的是 $X_4$ 。

我们发现频率系数1-7的的余弦波都有相对应的峰值索引，那剩余的频率系数为0的余弦波，由之前的上下平移变换可以得知，它对应的是索引为0的DCT系数。实际上频率为0的余弦波其实就是常值信号， $cos (0) = 1$ 。如果放到图像上来看，它其实就是一组图像的整体亮度，一组像素的整体亮度越高，那么它的索引为0的DCT系数就越大。反之越低。

实际上，每个频率都对应着一种图像模式，DCT所做的就是分解出各个基本模式，并计算它们对于原始图像的贡献：

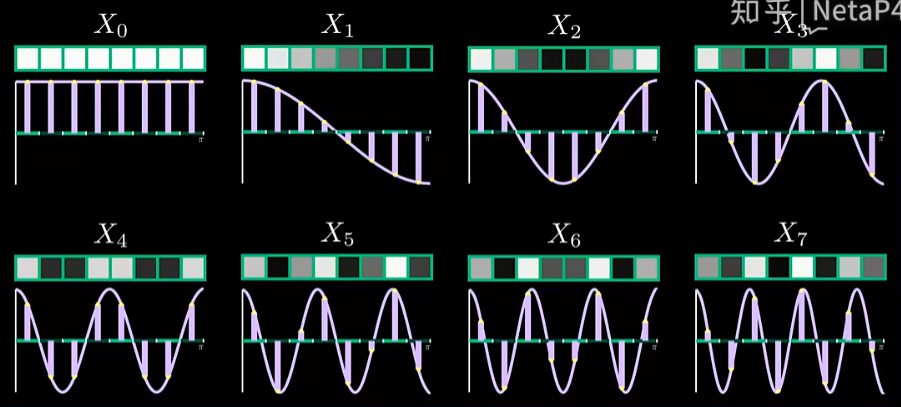
下面我们将通过数学公式看到，8个像素值的所有可能组合都可以表示为这8个余弦波的总和。

DCT数学原理

正变换

DCT系数的公式如下：

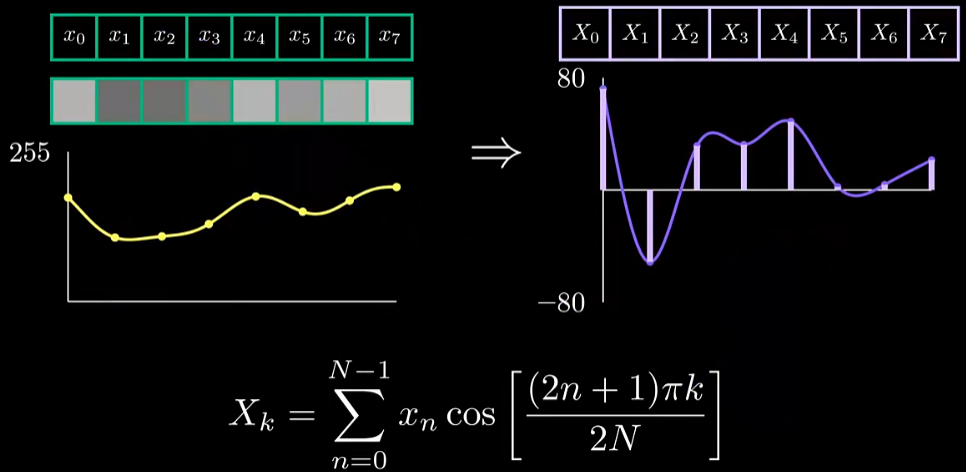
我们可以发现公式中的余弦函数和最开始我们定义的余弦函数采样点相同，那么DCT各个分量系数实际上就表示为原始信号的采样点与余弦波的样本点之积

为什么要做积呢，我们将公式换一种写法很容易就可以理解：

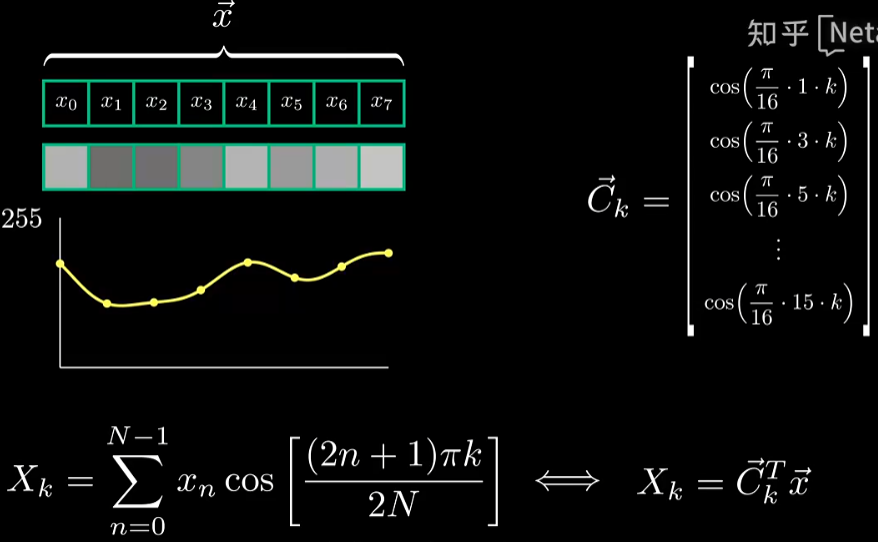
实际上就是余弦信号采样点与原始信号向量做了点积，而我们知道点积是衡量向量相关性的一个重要方法。这就是为什么我们之前对频率系数为 $k$ 的余弦信号采样，做DCT变换后，其峰值在 $X_k$ 处，因为两个向量是完全相同的，所以其点积也是最大的。

更一般地，我们可以将DCT变换写成余弦分量矩阵和原始信号向量乘积的形式：

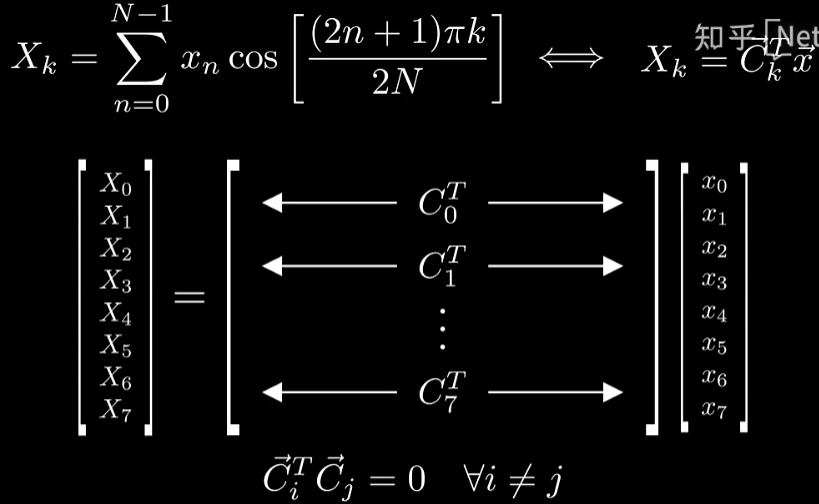
这个计算实质上就是一个简单的对原始信号的线性变换，但余弦信号分量矩阵具有重要的性质，那就是两两不同行相互正交，这也解释了为什么在前面的实验中，当我们向DCT输入一个特定频率的余弦信号时，只有一个峰值，而其他的系数都是0。

逆变换

DCT变换的一个重要性质就是它是可逆的，由DCT系数我们可以无损地还原出原始信号。由正变换的矩阵形式，我们很容易就可以得出逆变换是怎样的：

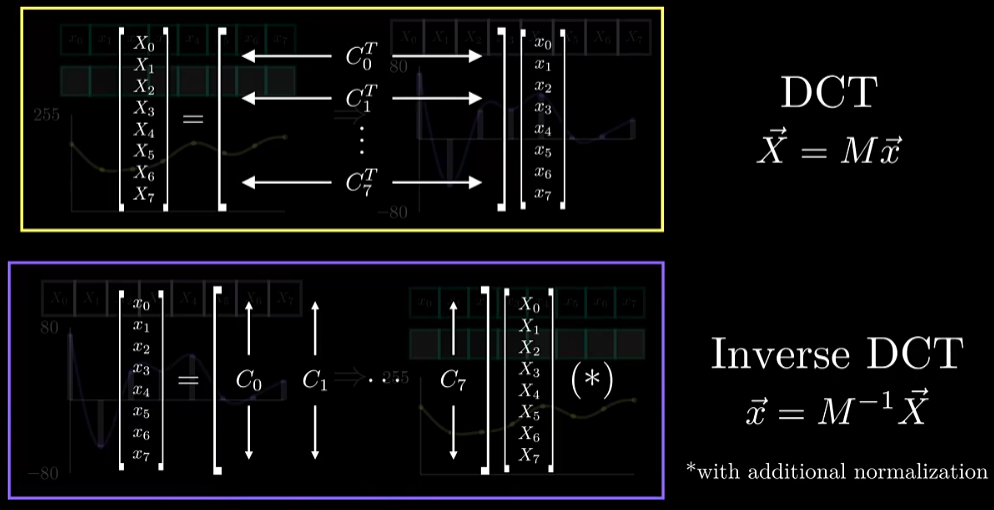
很重要的一点是，由于余弦分量矩阵不同行之间两两正交，所以它是一个近正交矩阵（ $AA^T=kE$ ），正交矩阵的逆就等于其转置，由于一个相同行相乘不一定等于1，所以在求逆时我们只需要用其转置再乘以一个归一化系数即可。

DCT逆变换实质上就是对余弦波进行线性组合，由于8个余弦波是两两正交的，就相当于一组基，所以任意8个原始信号采样都可以用这8个余弦波的线性组合表示。

实际应用

实际应用的时候，DCT变换采用如下公式：
$X(k)=\sqrt{2/N}·c(u)·\sum_{n=0}^{N-1}x(n)cos[\frac {k(2n+1)\pi} {2N}],k=0,1,...,N-1 \\ c(u) = \begin{cases} \frac 1 {\sqrt{2}} \hspace{5mm}&u=0\\ 1 & u>0 \end{cases}$
公式前部的 $\sqrt{2/N}·c(u)$ 是归一化系数，保证了余弦分量矩阵是正交的。可以进行测试：

%% DCT归一化系数 N=8
y(1,1:8) = sqrt(1/8);
for i = 1:7
    for j = 0:7
        y(i+1,j+1) = sqrt(2/8) * cos((2*j+1)*pi*i / 16);
    end
end
s = y*y'; %s=单位矩阵E

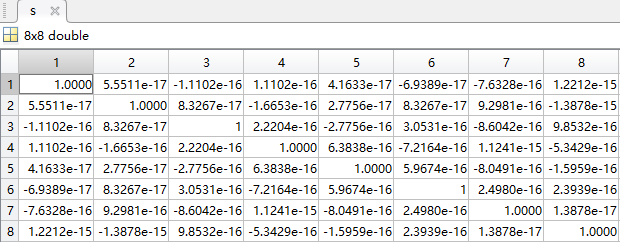
这里再介绍一个matlab中dctmtx的函数，该函数就是求DCT变换中归一化余弦分量矩阵的函数：

%% dctmtx函数测试
y(1,1:8) = sqrt(1/8);
for i = 1:7
    for j = 0:7
        y(i+1,j+1) = sqrt(2/8) * cos((2*j+1)*pi*i / 16);
    end
end
c = dctmtx(8); % 传入参数是N，即采样点数量

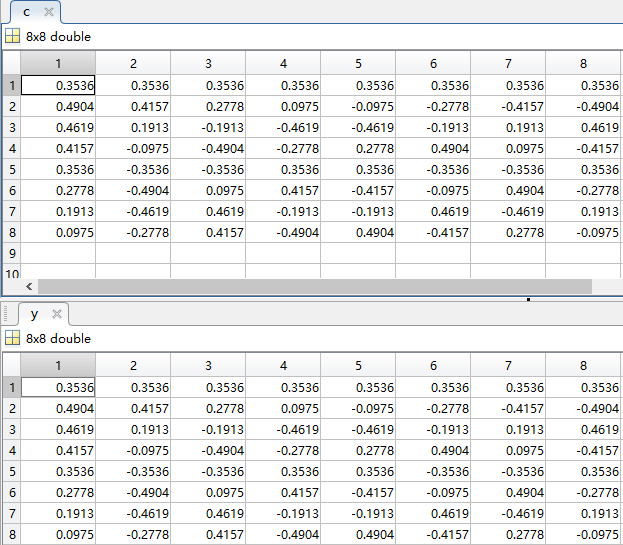
可以看到用dctmtx函数计算出的余弦分量矩阵与我们手动计算的完全相同。

二维DCT变换

前面介绍的一维DCT变换，那要应用于图像需要二维DCT变换，变换过程就是先对图像的每一行进行一维DCT变换得到一个DCT系数矩阵，再将这个DCT系数矩阵的每一列进行一维的DCT变换得到最终的二维DCT变换系数。（DCT变换的可分离性：也可以先列后行，经过数学证明结果是一样的）

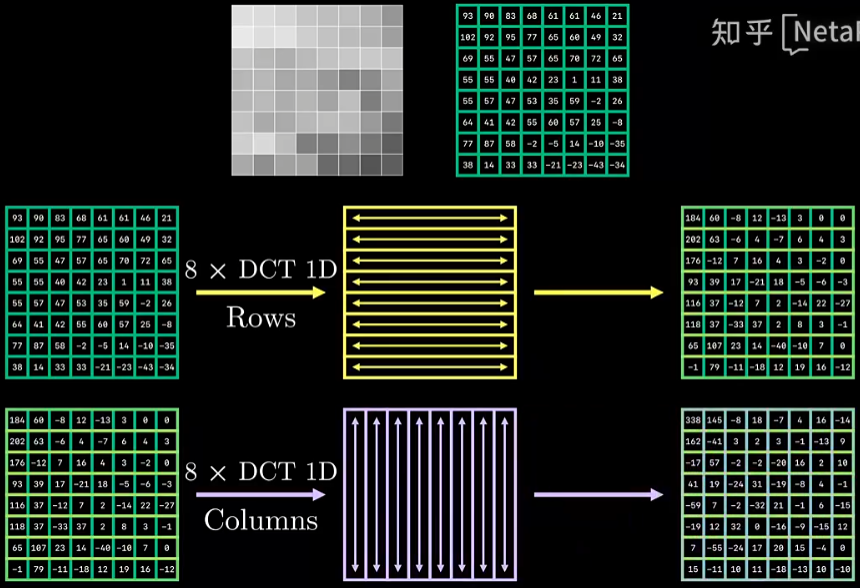
DCT变换还具有能量集中的性质，意思是DCT系数矩阵左上角的DCT系数通常较大，这是因为一般图像中大部分都是低频信号，高频信号（右下）只占一小部分，这也是为什么在JPEG压缩中，右下角都可以量化成0的原因，图像由一些低频信号就已经能够构建出大致的模样，这也是人眼最敏感的。

数学公式

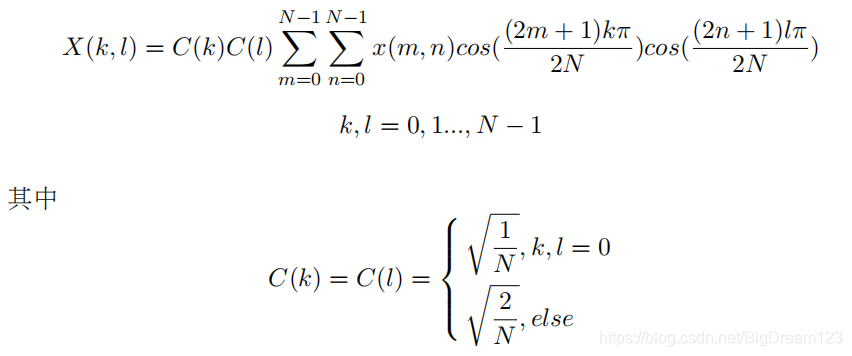
由于DCT变换具有可分离的性质，所以可以将二维DCT拆分成两个方向的一维DCT：

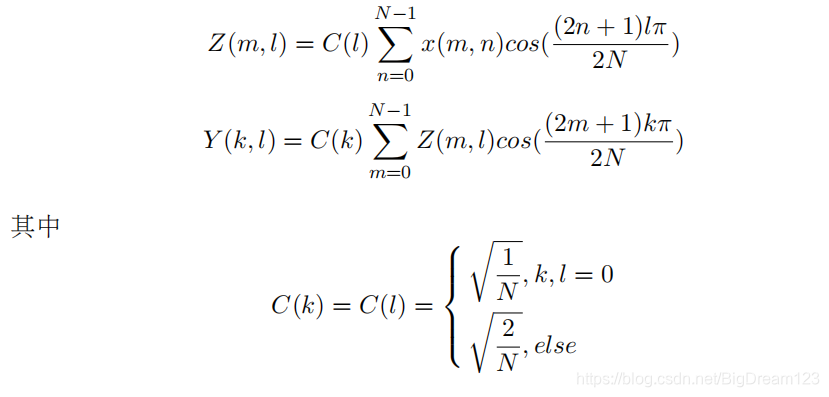
写成矩阵形式就是：

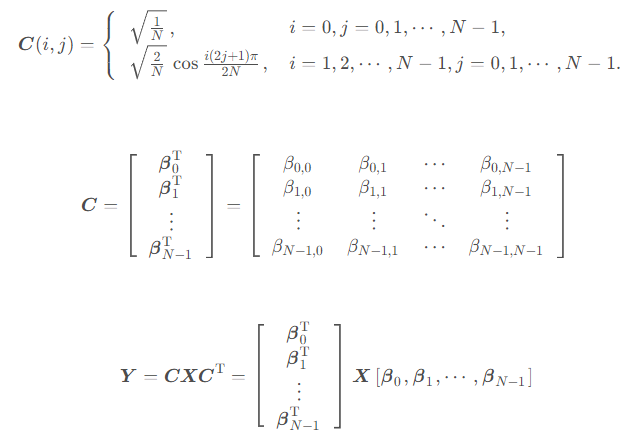
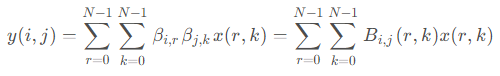
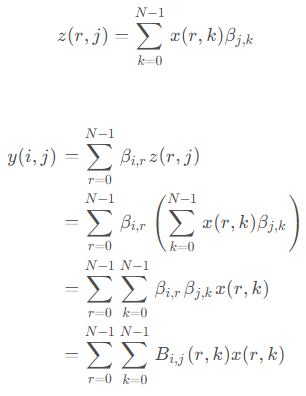
由于矩阵乘法具有结合律，所以 $Y=(CX)C^T=C(XC^T)$ ，表明无论是先对行做DCT再对列做DCT还是先对列做DCT再对行做DCT结果都一样。

基图像

上面公式中的 $B_{i,j}$ 即为基图像， $B_{i,j}=\beta_i \beta_j^T$ ，维度是 $N \times N$ ，共 $N \times N$ 种频率的基图像，使用基图像求DCT系数与进行两次一维DCT变换求DCT系数等价。

利用基图像进行2D DCT就是把对应频率的基图像和原始图像信号做逐像素乘积再对矩阵整体进行求和即可得到相应频率的DCT系数。

%% 二维DCT基图像
A = dctmtx(8);
B = A';
C = zeros(8, 8, 64);
m = 0;
for i = 1:8
    for j = 1:8
        m = m+1;
        C(:, :, m) = B(:, i)*A(j, :);
    end
end
minvalue = min(min(min(C)));
maxvalue = max(max(max(C)));
figure,
for k = 1:64
    subplot(8, 8, k)
    imshow(C(:, :, k), [minvalue, maxvalue]);
end

DCT在图像变换时的性质（可用于设计抗相似性变换的水印）

索引从0开始，有以下性质：

参考链接

[1] https://ww2.mathworks.cn/help/images/discrete-cosine-transform.html

[2] https://www.bilibili.com/video/BV1bc411q7YG/?spm_id_from=333.337.search-card.all.click&vd_source=bac8ddf04ec0b6386d58110f67353bc7

[3] https://blog.csdn.net/BigDream123/article/details/101426393

[4] https://blog.csdn.net/m0_51143578/article/details/129344131

[5] Guan H, Zeng Z, Liu J, et al. A novel robust digital image watermarking algorithm based on two-level DCT[C]//2014 International Conference on Information Science, Electronics and Electrical Engineering. IEEE, 2014, 3: 1804-1809.