单元积分点应力如何外插至节点上 | 数值实现篇

最新推荐文章于 2024-08-03 21:32:05 发布

易木木木响叮当

最新推荐文章于 2024-08-03 21:32:05 发布

阅读量727

点赞数 18

分类专栏：有限元编程文章标签： matlab

本文链接：https://blog.csdn.net/qq_45715554/article/details/139379437

版权

有限元编程专栏收录该内容

10 篇文章 1 订阅

订阅专栏

继上次的推文：有限元计算过程中积分点应力如何外插至节点处？【公式推导篇】，本次分享单元积分点应力外插至节点处的数值实现过程。

应力外插

核心理念：坐标系的转换。

假设$\left( \xi ,\eta \right) $是母单元的自然坐标系，$ \left( \hat{\xi},\hat{\eta} \right) $是由高斯积分点控制的坐标系（术语可能不专业），假设高斯积分方案为 $\times2$ 。坐标系转换关系：
$(\xi,\eta)=(\hat{\xi},\hat{\eta})/\sqrt{3}\quad\mathrm{or}\quad(\hat{\xi},\hat{\eta})=(\xi,\eta)\sqrt{3}$

单元内任一点的应力 $\sigma _P$ ，由4个高斯积分点应力 $\sigma _{Gi}$ 进行插值时，可表示为

$\sigma_{P}=\sum_{i=1}^{4}N_{i}\sigma_{Gi}=\begin{bmatrix}N_{1}(\hat{\xi},\hat{\eta})N_{2}(\hat{\xi},\hat{\eta})N_{3}(\hat{\xi},\hat{\eta})N_{4}(\hat{\xi},\hat{\eta})\end{bmatrix}\begin{bmatrix}\sigma_{G1}\\\sigma_{G2}\\\sigma_{G3}\\\sigma_{G4}\end{bmatrix}$

其中， $N(\hat{\xi},\hat{\eta})$ 是基于高斯积分点的形函数，第一个积分点的坐标在母单元坐标系下为（-1，-1），根据上述的坐标系转换的方式，在高斯积分点的坐标系下，第一个单元节点在高斯积分点坐标系下坐标为$\left( -\sqrt{3},-\sqrt{3} \right) $，将此坐标值代入第一个形函数，得 $1+\frac{\sqrt{3}}{2}$ ，相同的道理，可推导至四个节点在4个形函数下的 $\times 4$ 外插矩阵：

$\begin{bmatrix}\sigma_1\\\sigma_2\\\sigma_3\\\sigma_4\end{bmatrix}=\begin{bmatrix}1+0.5\sqrt{3}&-0.5&1-0.5\sqrt{3}&-0.5\\-0.5&1+0.5\sqrt{3}&-0.5&1-0.5\sqrt{3}\\1-0.5\sqrt{3}&-0.5&1+0.5\sqrt{3}&-0.5\\-0.5&1-0.5\sqrt{3}&-0.5&1+0.5\sqrt{3}\end{bmatrix}\begin{bmatrix}\sigma_{G1}\\\sigma_{G2}\\\sigma_{G3}\\\sigma_{G4}\end{bmatrix}$

数值实现

借助以上理论，我们可以基于matlab平台编制以下代码段：

% 将积分点应力外插至单元节点上，这里只列举了Q4的情况
for i = 1:3
  StressElem(e,:,i) = [1+0.5*sqrt(3) -0.5 1-0.5*sqrt(3) -0.5;
  -0.5 1+0.5*sqrt(3) -0.5 1-0.5*sqrt(3);
  1-0.5*sqrt(3) -0.5 1+0.5*sqrt(3) -0.5;
  -0.5 1-0.5*sqrt(3) -0.5 1+0.5*sqrt(3)]*...
  [stress(e,1,i);stress(e,2,i);stress(e,3,i);stress(e,4,i)];
end

对标Abaqus

模型材料参数为普通的线弹性材料，单元类型选择CPS4，网格划分及边界条件设置如下：

在结果对标过程中，可以先对比自研程序与Abaqus的节点位移场：

Abaqus位移场结果

自研程序位移场结果

在位移场一致的前提下，我们再来对标应力结果。以常见的mises应力为例：

Abaqus位移应力场结果

自研程序应力场结果

结果是一致的，说明了程序的正确性。

如果我们还想看一下细节方面的，以1号单元的节点应力 $s_{11}$ 为例：

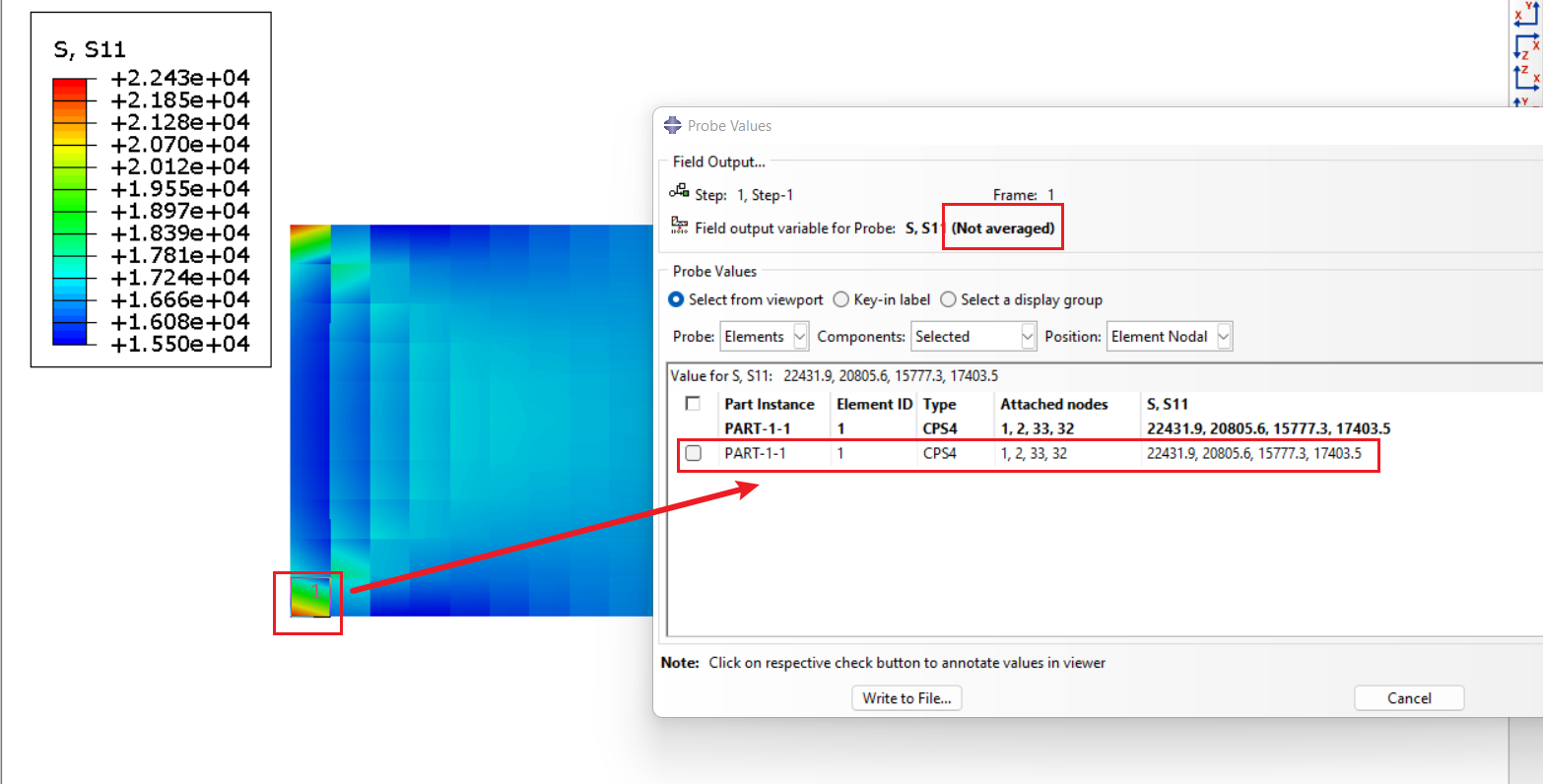
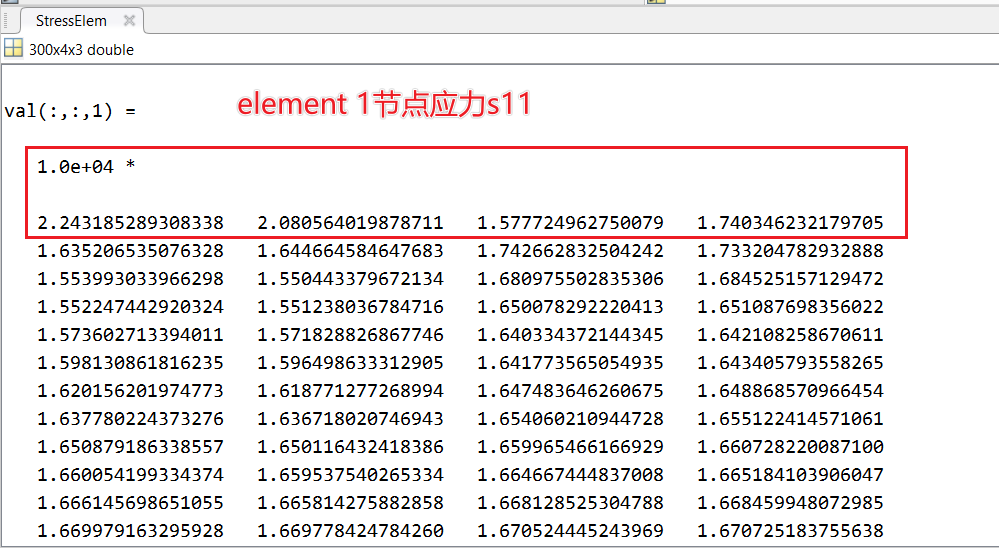
自研程序与Abaqus的结果也是一致的，在提取Abaqus单元节点应力时，应该将应力平滑选项取消勾选，即：

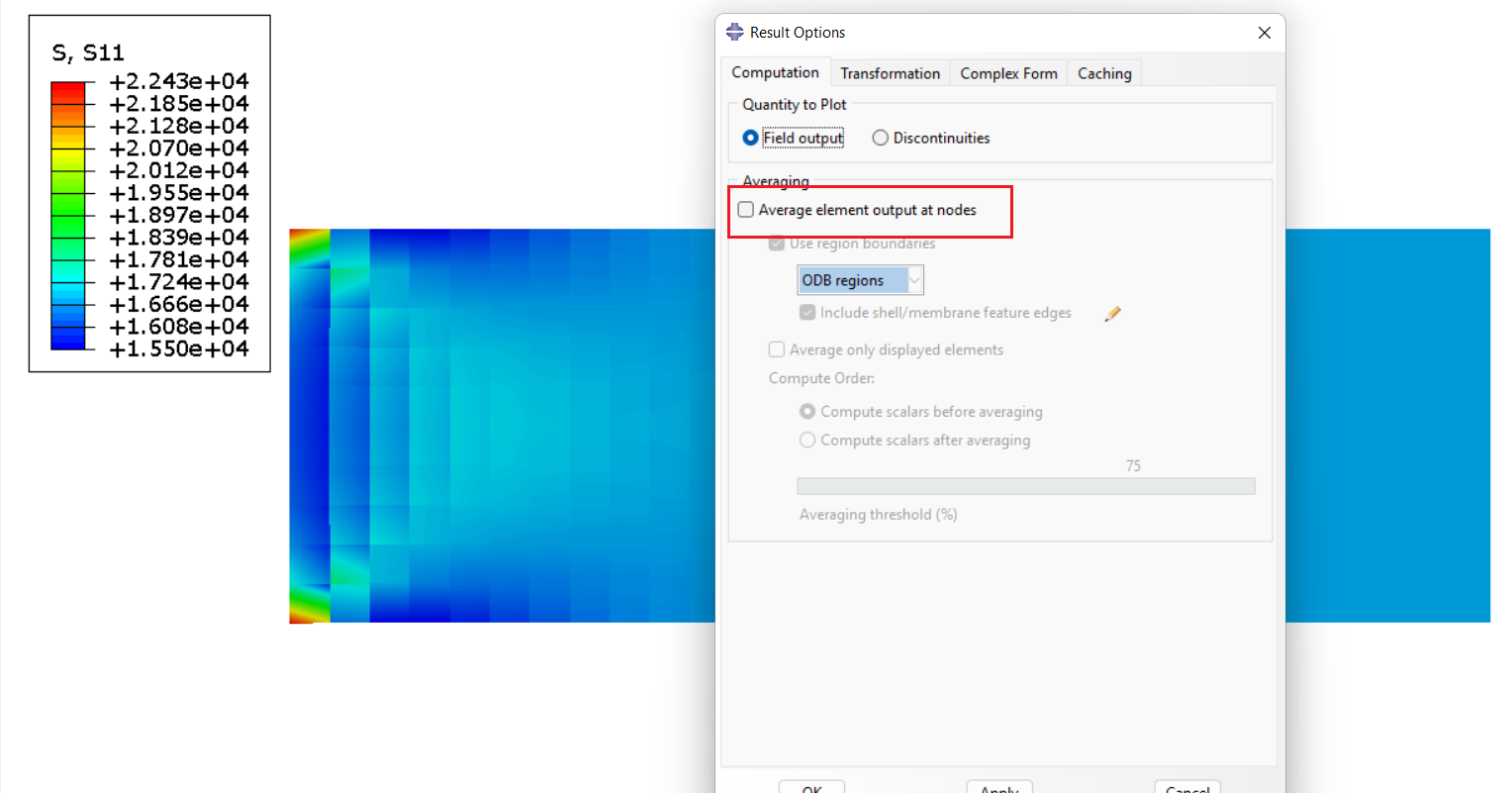
单元积分点应力外插matlab函数

function [StressElem,StressNode] = QuadNodeStress(node, element, prop, U, averageType,elemType,guassType)
% 通过节点位移计算节点应力，正应力：Sxx、Syy、Sxy、VonMises
% 增加节点应力均匀化标识：averageType，==1时，采用绕节点直接平均，==2时采用绕节点面积加权平均
    E = prop(1);
    NU = prop(2);
    ID = prop(4);

    [numberNodes, ~] = size(node);
    [numberElements, ~] = size(element);
    StressElem = zeros(numberElements, 3); % 只计算出正应力Sxx、Syy、Sxy即可
    StressNode = zeros(numberNodes, 4);
    WeightSum = zeros(numberNodes, 1);  % 用于加权平均的权重总和
    % 根据平面应力/应变状态ID选择应力-应变矩阵
    if ID == 1
        D = (E/(1-NU^2)) * [1, NU, 0; NU, 1, 0; 0, 0, (1-NU)/2];
    elseif ID == 2
        D = (E/(1+NU)/(1-2*NU)) * [1-NU, NU, 0; NU, 1-NU, 0; 0, 0, (1-2*NU)/2];
    end

    % quadrature according to quadType
    [gaussWeights,gaussLocations_cols]=gauss(guassType);
    stress = zeros(numberElements,size(gaussLocations_cols,1),3);
    StressElem = zeros(numberElements,4,3);
    elementDof = zeros(1,2*4);
    % 遍历所有单元计算单元应力
    for e = 1:numberElements
        indice = element(e,:);
        elementDof(1:2:end)=2*indice-1;
        elementDof(2:2:end)=2*indice;
        elementNode = element(e, :);
        elemNodeCoordinate = node(elementNode, :);
        elenode = length(elemNodeCoordinate);
        B=zeros(3,2*elenode);
        for q = 1:size(gaussWeights,1)
            xi_Gauss=gaussLocations_cols(q,1);
            eta_Gauss=gaussLocations_cols(q,2);
            % shape functions and derivatives
            [shapeFunction,naturalDerivatives]=shapeFunctionQuad(xi_Gauss,eta_Gauss,elemType);
            % Jacobian matrix, inverse of Jacobian,
            % derivatives w.r.t. x,y
            [Jacob,XYderivatives] = Jacobian(elemNodeCoordinate,naturalDerivatives);
            A = det(Jacob)*4;
            % B matrix
            B(1,1:2:end) = XYderivatives(:,1)';
            B(2,2:2:end) = XYderivatives(:,2)';
            B(3,1:2:end) = XYderivatives(:,2)';
            B(3,2:2:end) = XYderivatives(:,1)';
            % element deformation
            strain = B*U(elementDof);
            stress(e,q,1:3) = D*strain;
        end

        % 计算单元应力
        % 将积分点应力外插至单元节点上，这里只列举了Q4的情况
        for i = 1:3
            StressElem(e,:,i) = [1+0.5*sqrt(3) -0.5 1-0.5*sqrt(3) -0.5;
            -0.5 1+0.5*sqrt(3) -0.5 1-0.5*sqrt(3);
            1-0.5*sqrt(3) -0.5 1+0.5*sqrt(3) -0.5;
            -0.5 1-0.5*sqrt(3) -0.5 1+0.5*sqrt(3)]*...
            [stress(e,1,i);stress(e,2,i);stress(e,3,i);stress(e,4,i)];
        end
...