FPGA-Verilog实例----线性反馈移位寄存器（LFSR）

一、概述

线性反馈移位寄存器（LFSR）的英文全称为：Linear Feedback Shift Register
是移位寄存器的一种，通常用于在数字电路中产生伪随机数
通过一定的算法对事先选定的随机种子(seed)做一定的运算（选取哪些位置 用于移位，是需要进行预先设计好的）可以得到一组人工生成的周期序列，在这组序列中以相同的概率选取其中一个数字，该数字称作伪随机数。
这里的“伪”的含义是，由于该随机数是按照一定算法模拟产生的，其结果是确定的，是可见的，因此并不是真正的随机数。伪随机数的选择是从随机种子开始的，所以为了保证每次得到的伪随机数都足够地“随机”，随机种子的选择就显得非常重要，如果随机种子一样，那么同一个随机数发生器产生的随机数也会一样。

LFSR代表线性反馈移位寄存器，它是一种在FPGA内部有用的设计。 LFSR易于合成，这意味着它们占用的资源相对较少，并且可以在FPGA内部以很高的时钟速率运行。 使用LFSR可以使许多应用受益，包括：

计数器（Counters）
测试码型发生器（Test Pattern Generators）
数据加扰（Data Scrambling）
密码学（Cryptography）

二、原理

1. 线性反馈移位寄存器实现为FPGA内部的一系列触发器，这些触发器连接在一起作为移位寄存器。 影响下一个状态的比特位叫做抽头，移位寄存器链的多个抽头用作XOR或XNOR门的输入。 然后，此门的输出用作对移位寄存器链开始的反馈，因此用作LFSR中的反馈。

2. 运行LFSR时，由各个触发器生成的模式是伪随机的，这意味着它接近随机。 它不是完全随机的，因为从LFSR模式的任何状态，您都可以预测下一个状态。 有一些重要的移位寄存器属性需要注意：

👀 LFSR模式是伪随机的。
👀输出模式是确定性的。 您可以通过了解XOR门的位置以及当前模式来确定下一个状态。当抽头使用XOR门时，全0的模式不会出现。 由于0与0异或将始终产生0，因此LFSR将停止运行。
👀当抽头使用XNOR门时，全1的模式将不会出现。 由于将1与1进行异或运算将始终产生1，因此LFSR将停止运行。
👀任何LFSR的最大可能迭代次数= 2^Bits-1

3. 更长的LFSR将花费更长的时间来运行所有迭代。 N位LFSR的最大可能迭代次数为2^N-1。
   因此，对于3位，需要2^3-1 = 7个时钟来运行所有可能的组合;
   对于4位：2^4-1 = 15;
   对于5位：2^5-1 = 31，依此类推。
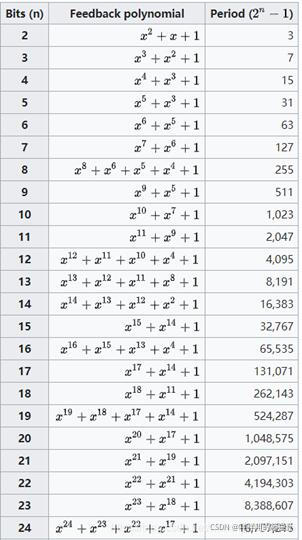
   这是Xilinx发布的所有LFSR模式的完整表（第五页）
   这里也有一张当N较小时的简短图
   
4. LFSR分为两种：
   一种是IE型的LFSR，即异或门内接的线性反馈移位寄存器，如下图第一张；
   另一种是EE型LFSR，即异或门外接的线性反馈移位寄存器，如下图第二张；
   这两种类型在代码表现上是不一样的：
   第一种LFSR的任何一位，如果g=1，其下一时刻值就是输出位以及其前一位的异或。
   第二种LFSR的任何一位，如果g=1，其下一时刻值就是其前一位的值，但是输入位的值，就需要其参与异或得到。

其中，gn为反馈系数，取值只能为0或1，取为0时表明不存在该反馈之路，取为1时表明存在该反馈之路，n个D触发器最多可以提供2^n-1个状态(不包括全0的状态)。为了保证这些状态没有重复，gn的选择必须满足一定的条件。

5. 结合第3点和第4点，我们来研究讨论一下如何进行反馈以及产生随机数
反馈系数的判断：完整表中的XNOR form 中的数字，或前面表格X的指数，以最大数字或最高指数为二进制码的最高位补全二进制数，然后再在末尾加1。
例如：
当n=3，补全对应的二进制位：1101，则 g0=1,g1=1,g2=0,g3=1；
当n=4，补全对应的二进制位：11001，则 g0=1,g1=1,g2=2,g3=0,g4=1;

笔者不才😭😭就手写举了一个例子进行说明

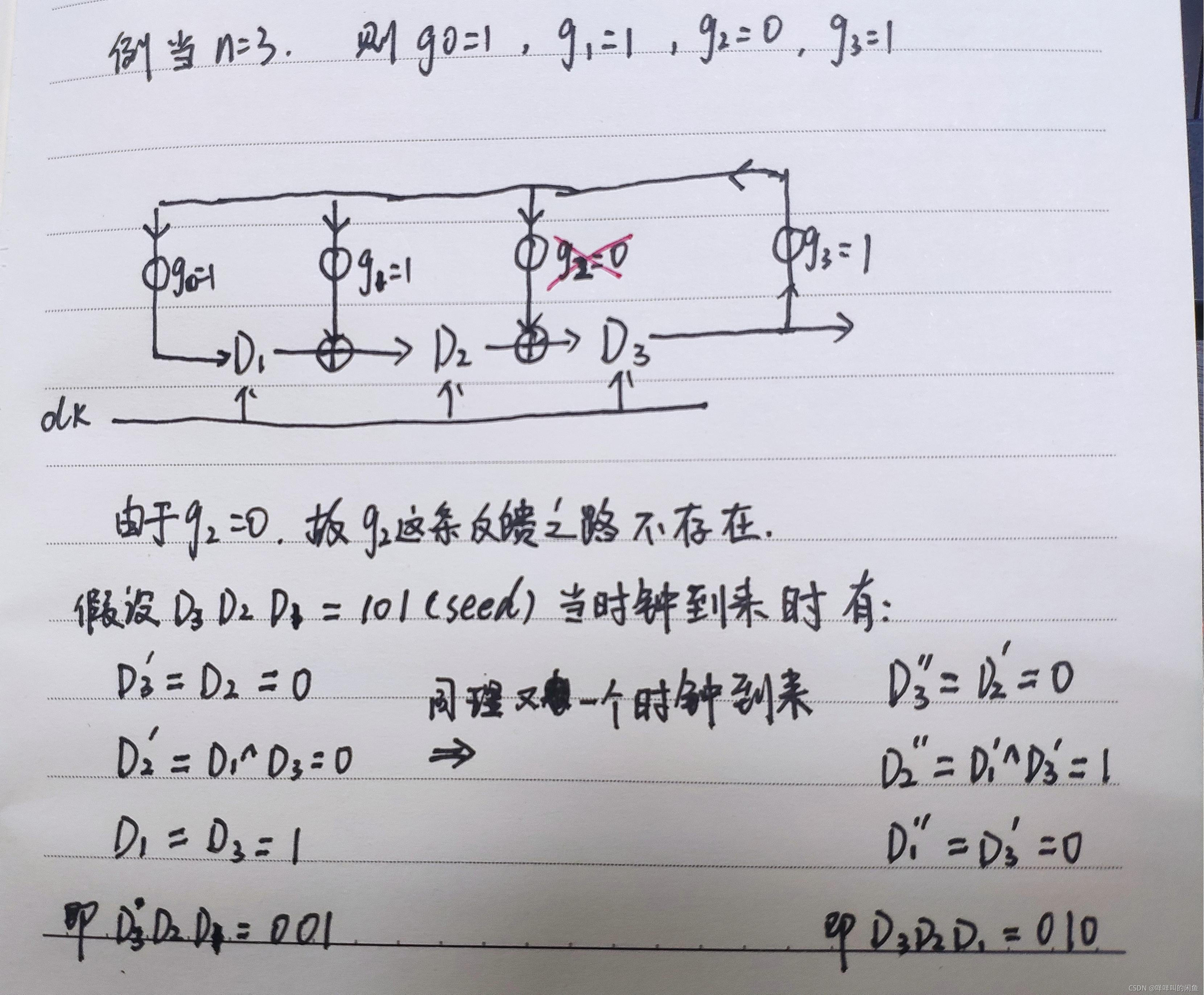
上图是是IE型的LFSR的一个当n=3产生随机数的解释流程。

如果理解了IE型，那么EE型也就简单了。首先反馈系数是一样的判断。区别主要在于异或的位置不一样。EE型是后面的反馈全部异或后给输入位。

三、Verilog实现

1. 源文件代码

module lfsr (
    input           clk     ,
    input           rst_n   ,
    input   [7:0]   seed    ,//种子值
    input           start   ,

    output  [7:0]   dout    ,//输出计数值
    output          dout_vld //当计数值计到种子值时，拉高
);
/**************************************功能介绍***********************************
	Description:	8bit lfsr多项式 x^8 + x^6 + x^5 + x^4 + 1	
    对应的是 bit7 bit5 bit4 bit3 异或之后，输入给bit0。
    斐波那契型(EE型)lfsr。
*********************************************************************************/

//信号定义

    reg     [7:0]       cnt         ;//count
    wire                xor_bit     ;

    reg                 start_r     ;
    wire                start_pedge ;

    always @(posedge clk or negedge rst_n)begin 
        if(!rst_n)begin
            start_r <= 0;
        end 
        else begin 
            start_r <= start;
        end 
    end

    assign start_pedge = start & ~start_r;//检测start的上升沿 上升沿有效时，加载种子值给计数器

    always @(posedge clk or negedge rst_n)begin //上升沿之后，当计数器使能时，产生数据输出
        if(!rst_n)begin
            cnt <= 0;
        end 
        else if(start_pedge)begin //检测到起始信号上升沿时，加载种子值
            cnt <= seed;
        end 
        else if(start_r)begin 
            cnt <= {cnt[6:0],xor_bit};
        end 
    end

    assign xor_bit = cnt[7]^cnt[5]^cnt[4]^cnt[3];
    
    //输出
    assign dout = cnt;
    assign dout_vld = start_r && cnt == seed;

endmodule

2. 仿真文件代码

`timescale 1ns/1ps  //定义时间尺度
                
module lfsr_tb();
//激励信号定义 
reg				clk  	;
reg				rst_n	;

reg     [7:0]	seed 	;
reg				start	;

//输出信号定义	 
wire	[7:0]	dout	;
wire            dout_vld;

                                          
//时钟周期参数定义					        
    parameter		CLOCK_CYCLE = 20;    
                                          
lfsr u_lfsr(
    .clk     (clk       ),
    .rst_n   (rst_n     ),
    .seed    (seed      ),//种子值
    .start   (start     ),
    .dout    (dout      ),//输出计数值
    .dout_vld(dout_vld  )
);
    
//产生时钟							       		
initial 		clk = 1'b0;		       		
always #(CLOCK_CYCLE/2) clk = ~clk;  		
                                                   
//产生激励							       		
initial  begin						       		
    rst_n = 1'b0;								
    seed = 0;	
    start = 0;							
    #(CLOCK_CYCLE*20);				            
    rst_n = 1'b1;							
    seed = 8'b1001_1110;	
    start = 1'b1;	  
    #(CLOCK_CYCLE*500);                                             
    start = 1'b0;   
    #(CLOCK_CYCLE*20);      
    seed = 8'b1111_1010;	
    start = 1'b1;	    
    #(CLOCK_CYCLE*500);      
    $stop; 
    //$finish;                                        
                                                  
end 									       	
endmodule

3. 仿真波形
   
   以1001 1110为种子，在255个状态中循环，可将输出值58、117、234……作为伪随机数。

今天的分享就结束了，文章内容的不足之处，望大佬指点指点😍😍