树模型与集成学习(一)——决策树
- 习题1
- 证明 G ( Y , X ) = H ( X ) − H ( X ∣ Y ) G(Y,X)=H(X)-H(X|Y) G(Y,X)=H(X)−H(X∣Y)
- 证明 G ( Y , X ) = H ( X ) + H ( Y ) − H ( X , Y ) G(Y,X)=H(X)+H(Y)-H(X,Y) G(Y,X)=H(X)+H(Y)−H(X,Y)
- 证明 G ( Y , X ) = H ( Y , X ) − H ( X ∣ Y ) − H ( Y ∣ X ) G(Y,X)=H(Y,X)-H(X\vert Y)-H(Y\vert X) G(Y,X)=H(Y,X)−H(X∣Y)−H(Y∣X)
- 图片指代的区域
- 练习2
- 练习3
- 参考资料
本博客为Datawhale组织的开源学习记录博客
学习的内容链接:树模型与集成学习
习题1

证明 G ( Y , X ) = H ( X ) − H ( X ∣ Y ) G(Y,X)=H(X)-H(X|Y) G(Y,X)=H(X)−H(X∣Y)
由教案中,可得到如下公式
G
(
Y
,
X
)
=
H
(
Y
)
−
H
(
Y
∣
X
)
G(Y,X)=H(Y)−H(Y|X)
G(Y,X)=H(Y)−H(Y∣X)
G
(
Y
,
X
)
=
−
∑
k
=
1
K
∑
m
=
1
M
p
(
y
k
,
x
m
)
log
2
p
(
y
k
)
p
(
x
m
)
p
(
y
k
,
x
m
)
G(Y,X)=-\sum_{k=1}^K\sum_{m=1}^M p(y_k,x_m) \log_2\frac{p(y_k)p(x_m)}{p(y_k, x_m)}
G(Y,X)=−k=1∑Km=1∑Mp(yk,xm)log2p(yk,xm)p(yk)p(xm)
H
(
Y
)
=
−
∑
k
=
1
K
p
(
y
k
)
log
2
p
(
y
k
)
H(Y)=-\sum_{k=1}^K p(y_k)\log_2p(y_k)
H(Y)=−k=1∑Kp(yk)log2p(yk)
H
(
Y
∣
X
)
=
−
∑
m
=
1
M
p
(
x
m
)
∑
k
=
1
K
p
(
y
k
∣
X
=
x
m
)
log
2
p
(
y
k
∣
X
=
x
m
)
H(Y|X)=-\sum_{m=1}^Mp(x_m)\sum_{k=1}^K p(y_k\vert X=x_m)\log_2p(y_k\vert X=x_m)
H(Y∣X)=−m=1∑Mp(xm)k=1∑Kp(yk∣X=xm)log2p(yk∣X=xm)
因此,我们可得到如下公式
H
(
X
)
=
−
∑
m
=
1
M
p
(
x
m
)
log
2
p
(
x
m
)
H(X)=-\sum_{m=1}^M p(x_m)\log_2p(x_m)
H(X)=−m=1∑Mp(xm)log2p(xm)
H
(
X
∣
Y
)
=
−
∑
k
=
1
K
p
(
y
k
)
∑
m
=
1
M
p
(
x
m
∣
Y
=
y
k
)
log
2
p
(
x
m
∣
Y
=
y
k
)
H(X|Y)=-\sum_{k=1}^Kp(y_k)\sum_{m=1}^M p(x_m\vert Y=y_k)\log_2p(x_m\vert Y=y_k)
H(X∣Y)=−k=1∑Kp(yk)m=1∑Mp(xm∣Y=yk)log2p(xm∣Y=yk)
则
H
(
X
)
−
H
(
X
∣
Y
)
=
−
∑
m
=
1
M
p
(
x
m
)
log
2
p
(
x
m
)
+
−
∑
k
=
1
K
p
(
y
k
)
∑
m
=
1
M
p
(
x
m
∣
Y
=
y
k
)
log
2
p
(
x
m
∣
Y
=
y
k
)
=
−
∑
m
=
1
M
[
∑
k
=
1
K
p
(
y
k
,
x
m
)
]
log
2
p
(
x
m
)
+
∑
m
=
1
M
∑
k
=
1
K
p
(
y
k
)
p
(
y
k
,
x
m
)
p
(
y
k
)
log
2
p
(
y
k
,
x
m
)
p
(
y
k
)
=
∑
m
=
1
M
∑
k
=
1
K
p
(
y
k
,
x
m
)
[
log
2
p
(
y
k
,
x
m
)
p
(
y
k
)
−
log
2
p
(
x
m
)
]
=
−
∑
k
=
1
K
∑
m
=
1
M
p
(
y
k
,
x
m
)
log
2
p
(
y
k
)
p
(
x
m
)
p
(
y
k
,
x
m
)
=
G
(
Y
,
X
)
\begin{aligned} H(X)-H(X|Y)&=-\sum_{m=1}^M p(x_m)\log_2p(x_m)+-\sum_{k=1}^Kp(y_k)\sum_{m=1}^M p(x_m\vert Y=y_k)\log_2p(x_m\vert Y=y_k) \\ &=-\sum_{m=1}^M[\sum_{k=1}^Kp(y_k, x_m)]\log_2p(x_m)+\sum_{m=1}^M \sum_{k=1}^Kp(y_k)\frac{p(y_k, x_m)}{p(y_k)}\log_2\frac{p(y_k, x_m)}{p(y_k)}\\ &=\sum_{m=1}^M \sum_{k=1}^Kp(y_k,x_m)[\log_2\frac{p(y_k, x_m)}{p(y_k)}-\log_2p(x_m)] \\ &=-\sum_{k=1}^K\sum_{m=1}^M p(y_k,x_m) \log_2\frac{p(y_k)p(x_m)}{p(y_k, x_m)}\\ &=G(Y,X) \end{aligned}
H(X)−H(X∣Y)=−m=1∑Mp(xm)log2p(xm)+−k=1∑Kp(yk)m=1∑Mp(xm∣Y=yk)log2p(xm∣Y=yk)=−m=1∑M[k=1∑Kp(yk,xm)]log2p(xm)+m=1∑Mk=1∑Kp(yk)p(yk)p(yk,xm)log2p(yk)p(yk,xm)=m=1∑Mk=1∑Kp(yk,xm)[log2p(yk)p(yk,xm)−log2p(xm)]=−k=1∑Km=1∑Mp(yk,xm)log2p(yk,xm)p(yk)p(xm)=G(Y,X)
原公式得证
证明 G ( Y , X ) = H ( X ) + H ( Y ) − H ( X , Y ) G(Y,X)=H(X)+H(Y)-H(X,Y) G(Y,X)=H(X)+H(Y)−H(X,Y)
由题干可知:
E
(
Y
,
X
)
∼
p
(
y
,
x
)
[
−
log
2
p
(
Y
,
X
)
]
\mathbb{E}_{(Y,X)\sim p(y,x)}[-\log_2p(Y,X)]
E(Y,X)∼p(y,x)[−log2p(Y,X)]
则
H
(
X
,
Y
)
=
−
∑
m
=
1
M
∑
k
=
1
K
p
(
x
m
,
y
k
)
log
2
p
(
x
m
,
y
k
)
H(X,Y)=-\sum_{m=1}^M \sum_{k=1}^K p(x_m,y_k)\log_2p(x_m,y_k)
H(X,Y)=−m=1∑Mk=1∑Kp(xm,yk)log2p(xm,yk)
则
H
(
Y
∣
X
)
=
−
∑
m
=
1
M
p
(
x
m
)
∑
k
=
1
K
p
(
y
k
∣
X
=
x
m
)
log
2
p
(
y
k
∣
X
=
x
m
)
=
−
∑
k
=
1
K
∑
m
=
1
M
p
(
x
m
)
p
(
y
k
,
x
m
)
p
(
x
m
)
log
2
p
(
y
k
,
x
m
)
p
(
x
m
)
=
∑
k
=
1
K
∑
m
=
1
M
p
(
x
m
)
p
(
y
k
,
x
m
)
p
(
x
m
)
log
2
p
(
x
m
)
−
∑
k
=
1
K
∑
m
=
1
M
p
(
x
m
)
p
(
y
k
,
x
m
)
p
(
x
m
)
log
2
p
(
y
k
,
x
m
)
=
∑
m
=
1
M
p
(
x
m
)
log
2
p
(
x
m
)
−
∑
m
=
1
M
∑
k
=
1
K
p
(
x
m
,
y
k
)
log
2
p
(
x
m
,
y
k
)
=
−
H
(
X
)
+
H
(
X
,
Y
)
)
\begin{aligned} H(Y|X)&=-\sum_{m=1}^Mp(x_m)\sum_{k=1}^K p(y_k\vert X=x_m)\log_2p(y_k\vert X=x_m)\\ &=-\sum_{k=1}^K\sum_{m=1}^M p(x_m)\frac{p(y_k, x_m)}{p(x_m)}\log_2\frac{p(y_k, x_m)}{p(x_m)}\\ &=\sum_{k=1}^K\sum_{m=1}^M p(x_m)\frac{p(y_k, x_m)}{p(x_m)}\log_2{p(x_m)}-\sum_{k=1}^K\sum_{m=1}^M p(x_m)\frac{p(y_k, x_m)}{p(x_m)}\log_2{p(y_k, x_m)}\\ &=\sum_{m=1}^M p(x_m)\log_2p(x_m)-\sum_{m=1}^M \sum_{k=1}^K p(x_m,y_k)\log_2p(x_m,y_k)\\ &=-H(X)+H(X,Y))\\ \end{aligned}
H(Y∣X)=−m=1∑Mp(xm)k=1∑Kp(yk∣X=xm)log2p(yk∣X=xm)=−k=1∑Km=1∑Mp(xm)p(xm)p(yk,xm)log2p(xm)p(yk,xm)=k=1∑Km=1∑Mp(xm)p(xm)p(yk,xm)log2p(xm)−k=1∑Km=1∑Mp(xm)p(xm)p(yk,xm)log2p(yk,xm)=m=1∑Mp(xm)log2p(xm)−m=1∑Mk=1∑Kp(xm,yk)log2p(xm,yk)=−H(X)+H(X,Y))
根据
H
(
Y
∣
X
)
=
−
H
(
X
)
+
H
(
X
,
Y
)
H(Y|X)=-H(X)+H(X,Y)
H(Y∣X)=−H(X)+H(X,Y)和
G
(
Y
,
X
)
=
H
(
Y
)
−
H
(
Y
∣
X
)
G(Y,X)=H(Y)−H(Y|X)
G(Y,X)=H(Y)−H(Y∣X),可得
G
(
Y
,
X
)
=
H
(
X
)
+
H
(
Y
)
−
H
(
X
,
Y
)
G(Y,X)=H(X)+H(Y)-H(X,Y)
G(Y,X)=H(X)+H(Y)−H(X,Y)
证明 G ( Y , X ) = H ( Y , X ) − H ( X ∣ Y ) − H ( Y ∣ X ) G(Y,X)=H(Y,X)-H(X\vert Y)-H(Y\vert X) G(Y,X)=H(Y,X)−H(X∣Y)−H(Y∣X)
已知
G
(
Y
,
X
)
=
H
(
X
)
+
H
(
Y
)
−
H
(
X
,
Y
)
(1)
G(Y,X)=H(X)+H(Y)-H(X,Y)\tag{1}
G(Y,X)=H(X)+H(Y)−H(X,Y)(1)
G
(
Y
,
X
)
=
H
(
X
)
−
H
(
X
∣
Y
)
)
(2)
G(Y,X)=H(X)-H(X|Y))\tag{2}
G(Y,X)=H(X)−H(X∣Y))(2)
G
(
Y
,
X
)
=
H
(
Y
)
−
H
(
Y
∣
X
)
)
(3)
G(Y,X)=H(Y)−H(Y|X))\tag{3}
G(Y,X)=H(Y)−H(Y∣X))(3) ,(3)式+(2)式-(1)式,即可得:
G
(
Y
,
X
)
=
H
(
Y
,
X
)
−
H
(
X
∣
Y
)
−
H
(
Y
∣
X
)
G(Y,X)=H(Y,X)-H(X\vert Y)-H(Y\vert X)
G(Y,X)=H(Y,X)−H(X∣Y)−H(Y∣X)
图片指代的区域
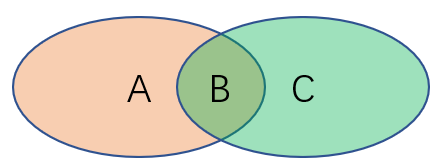
H ( X ) = A + B H ( Y ) = B + C H ( X ∣ Y ) = A H ( Y ∣ X ) = C H ( X , Y ) = A + B + C G ( X , Y ) = B H(X)=A+B\\ H(Y)=B+C\\ H(X|Y)=A\\ H(Y|X)=C\\ H(X,Y)=A+B+C\\ G(X,Y)=B H(X)=A+BH(Y)=B+CH(X∣Y)=AH(Y∣X)=CH(X,Y)=A+B+CG(X,Y)=B
练习2
假设当前我们需要处理一个分类问题,请问对输入特征进行归一化会对树模型的类别输出产生影响吗?请解释原因。
不会产生影响,树模型基于信息增益、信息增益率、基尼指数作为特征空间划分方法,任何特征的单调变换(不影响排序结果)均不会影响模型。
练习3
如果将系数替换为
1
−
γ
2
1-\gamma^2
1−γ2,请问对缺失值是加强了还是削弱了惩罚?
削弱了惩罚,例如
γ
=
0.5
\gamma=0.5
γ=0.5,信息增益从0.5变为0.75,变得更重要,因此削弱了惩罚。
参考资料
https://www.zhihu.com/question/389542211/answer/1169859488
练习4
【练习】如果将树的生长策略从深度优先生长改为广度优先生长,假设其他参数保持不变的情况下,两个模型对应的结果输出可能不同吗?
不会,深度优先和广度优先只是搜索的顺序不同,而最终的结果并不会发生改变。
练习5
【练习】在一般的机器学习问题中,我们总是通过一组参数来定义模型的损失函数,并且在训练集上以最小化该损失函数为目标进行优化。请问对于决策树而言,模型优化的目标是什么?
决策树的目的是从训练集中归纳出一组分类规则,这个决策树要尽可能与训练集不矛盾,同时具有较好的泛化能力。
为了实现上述目标,决策树的损失函数通常为正则化的极大似然函数。
练习6
【练习】对信息熵中的 log \log log函数在 p = 1 p=1 p=1处进行一阶泰勒展开可以近似为基尼系数,那么如果在 p = 1 p=1 p=1处进行二阶泰勒展开我们可以获得什么近似指标?请写出对应指标的信息增益公式。
log
\log
log函数在
p
=
1
p=1
p=1处进行泰勒二阶展开,则
H
(
Y
)
=
E
Y
I
(
p
)
=
E
Y
[
−
log
2
p
(
Y
)
]
≈
E
Y
[
p
(
Y
)
2
−
4
p
(
Y
)
+
3
2
]
H(Y)=\mathbb{E}_YI(p)=\mathbb{E}_Y[-\log_2p(Y)]\approx\mathbb{E}_Y[\cfrac{p(Y)^2-4p(Y)+3}{2}]
H(Y)=EYI(p)=EY[−log2p(Y)]≈EY[2p(Y)2−4p(Y)+3]
则
G
i
n
i
(
Y
)
=
E
Y
[
p
(
Y
)
2
−
4
p
(
Y
)
+
3
2
]
=
∑
k
=
1
K
p
~
(
y
k
)
(
p
~
2
(
y
k
)
−
4
p
~
(
y
k
)
+
3
2
)
=
1
2
(
∑
k
=
1
K
p
~
3
(
y
k
)
−
4
∑
k
=
1
K
p
~
2
(
y
k
)
+
3
)
\begin{aligned} {\rm Gini}(Y)&=\mathbb{E}_Y[\cfrac{p(Y)^2-4p(Y)+3}{2}]\\ &=\sum_{k=1}^K \tilde{p}(y_k)(\cfrac{{\tilde{p}^2(y_k)}-4{\tilde{p}(y_k)}+3}{2})\\ &=\cfrac{1}{2}(\sum_{k=1}^K\tilde{p}^3(y_k)-4\sum_{k=1}^K\tilde{p}^2(y_k)+3) \end{aligned}
Gini(Y)=EY[2p(Y)2−4p(Y)+3]=k=1∑Kp~(yk)(2p~2(yk)−4p~(yk)+3)=21(k=1∑Kp~3(yk)−4k=1∑Kp~2(yk)+3)
G i n i ( Y ∣ X ) = E X [ E Y ∣ X [ p ( Y ∣ X ) 2 − 4 p ( Y ∣ X ) + 3 2 ] ] = ∑ m = 1 M p ~ ( x m ) ∑ k = 1 K [ p ~ ( y k ∣ x m ) ( p ~ 2 ( y k ∣ x m ) − 4 p ~ ( y k ∣ x m ) + 3 2 ) ] = = 1 2 ∑ m = 1 M p ~ ( x m ) [ ∑ k = 1 K p ~ 3 ( y k ∣ x m ) − 4 ∑ k = 1 K p ~ 2 ( y k ∣ x m ) + 3 ] \begin{aligned} {\rm Gini}(Y\vert X)&=\mathbb{E}_X[\mathbb{E}_{Y\vert X}[\cfrac{p(Y\vert X)^2-4p(Y\vert X)+3}{2}]]\\ &=\sum_{m=1}^M \tilde{p}(x_m)\sum_{k=1}^K[\tilde{p}(y_k\vert x_m)(\cfrac{{\tilde{p}^2(y_k\vert x_m)}-4{\tilde{p}(y_k\vert x_m)}+3}{2})]\\ &==\cfrac{1}{2}\sum_{m=1}^M \tilde{p}(x_m)[\sum_{k=1}^K\tilde{p}^3(y_k\vert x_m)-4\sum_{k=1}^K\tilde{p}^2(y_k\vert x_m)+3] \end{aligned} Gini(Y∣X)=EX[EY∣X[2p(Y∣X)2−4p(Y∣X)+3]]=m=1∑Mp~(xm)k=1∑K[p~(yk∣xm)(2p~2(yk∣xm)−4p~(yk∣xm)+3)]==21m=1∑Mp~(xm)[k=1∑Kp~3(yk∣xm)−4k=1∑Kp~2(yk∣xm)+3]
G ( Y , X ) = G i n i ( Y ) − G i n i ( Y ∣ X ) G(Y,X)={\rm Gini}(Y)-{\rm Gini}(Y\vert X) G(Y,X)=Gini(Y)−Gini(Y∣X)
练习7
【练习】除了信息熵和基尼系数之外,我们还可以使用节点的 ( 1 − max k p ( Y = y k ) (1-\max_{k}p(Y=y_k) (1−maxkp(Y=yk)和第m个子节点的 ( 1 − max k p ( Y = y k ∣ X = x m ) (1-\max_{k}p(Y=y_k\vert X=x_m) (1−maxkp(Y=yk∣X=xm)来作为衡量纯度的指标。请解释其合理性并给出相应的信息增益公式。
节点的 ( 1 − max k p ( Y = y k ) (1-\max_{k}p(Y=y_k) (1−maxkp(Y=yk)和第m个子节点的 ( 1 − max k p ( Y = y k ∣ X = x m ) (1-\max_{k}p(Y=y_k\vert X=x_m) (1−maxkp(Y=yk∣X=xm)其实就是分类中常用的错分率,好的模型要尽可能减少错分率,与信息熵的减少的目标一致。
信息增益公式 G ( Y , X ) = max k p ( Y = y k ∣ X = x m ) − max k p ( Y = y k ) G(Y,X)=\max_{k}p(Y=y_k\vert X=x_m)-\max_{k}p(Y=y_k) G(Y,X)=kmaxp(Y=yk∣X=xm)−kmaxp(Y=yk)
练习8
【练习】为什么对没有重复特征值的数据,决策树能够做到损失为0?
当决策树的节点树过多,甚至对每个数据,都构建一个叶子节点。如果没有重复特征值,则训练集便会达到100%正确率,就会使得损失为0
练习9
【练习】如何理解min_samples_leaf参数能够控制回归树输出值的平滑程度?
叶子过多,导致过拟合,所以需要设置min_samples_leaf,控制过拟合,从而控制输出值的平滑程度。





















 456
456











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








