信号与系统——离散时间系统的建模及仿真

摘要

在本次实验中，我们首先完成了对于固定金额利率，固定存取方式的建模仿真和计算，利用MATLAB得到了要求的余额变化图，并且对于此类模型的构建有了基本的了解。随后我们在问题的基础上对于非给定金额和存取方式的最大收益比进行了模拟，针对此类没有明确数学表达式的问题，我们采用了蒙特卡洛模拟的方法并且和我们经验结合，合理推论得到了最大化收益的方法。

关键词

存取款模型，MATLAB，蒙特卡洛模拟。

问题1------银行存款帐户余额每月变化情况的建模及仿真

考虑如下的问题：银行月息1%，起始金额1000元。前两年（24个月）每月存入
100元（该部分款项从下月开始计息），从第三年起不再存入，每月从账户中取出500元。
由此我们可以判断，这是一个DT系统，我们首先确定他的系统方程。

建立该离散时间系统的数学模型

在建模之前，我们首先做一些必要的假设和字符的说明：

1. 设定利息在每月月末结算，当月存入的款项将从下月开始计算利息；

2. 存取都在每月的月初进行；

3. 我们设y[n]表示每月月末结算利之后的余额，用x[n]表示每月的存取。即前者是系统响应的结果，后者是系统的输入。

由上边的假设，我们可以得到式子：$y[n]=1.01y[n-1]+x[n]$，其中y[0]=1000。在$n\in [1,24]$时，x[n]=100。

在存款的时候，月初存入的要在下月开始计算利息，但是在取款的时候，月初取出的不应再计入当月的利息，所以在$n>24$的时候$y[n]=1.01(y[n-1]+x[n])$，x[n]=-500。

综上所述，我们写出总的输入和系统函数：

$$x[n]=\{\begin{array}{r}100,n\in [1,24]\\ -500,n>25\end{array}$$

$$y[n]=\{\begin{array}{r}1.01y[n-1]+x[n],n\in [1,24]\\ 1.01(y[n-1]+x[n]),n>25\end{array}$$

利用MATALAB计算每月帐户余额变动情况并画图

根据总的输入和系统函数：

$$x[n]=\{\begin{array}{r}100,n\in [1,24]\\ -500,n>25\end{array}$$

$$y[n]=\{\begin{array}{r}1.01y[n-1]+x[n],n\in [1,24]\\ 1.01(y[n-1]+x[n]),n>25\end{array}$$

我们可以编写MATLAB程序如下：

y=[]; %账户
y(1)=1000; %初始账户为1000 y[0]=1000但是MATLAB索引只能从1开始
Rate=0.01; %设置月利息
for n=2:25
    y(n)=(1+Rate)*y(n-1)+100; %对应设定的y[n]=1.01y[n-1]+x[n]
    fprintf('第%d个月结束后，账户的余额是%f\n',(n-1),y(n)) 
%n-1修正月数
end
disp("存款结束")

for i=1:n
    plot(i-1,y(i),'.');
    hold on
end
xlabel('月数')
ylabel('账户余额')
title('月利率1%时 账户余额变化') 
n=26; 
%存款结束后是24月末 对应数组的y(25)，则下一个应该是25月对应y(26)
while(1)
    if (1+Rate)*(y(n-1)-500)<0 
%当最后一个月不足500的时候，全部取出，让余额为0，结束循环
        y(n)=0;
        fprintf('第%d个月结束后，账户的余额是%f\n',(n-1),y(n))
        break
    else
        y(n)=(1+Rate)*(y(n-1)-500);
        fprintf('第%d个月结束后，账户的余额是%f\n',(n-1),y(n))
    end
    n=n+1;
end

for i=1:n
    plot(i-1,y(i),'.');
    hold on
end
xlabel('月数')
ylabel('账户余额')
title('月利率1%时 账户余额变化')

对应的输出如下：

我们可以很直观的看出，当在32月结束的时候，账户的余额只有111，在33月月初的时候，账户余额为0。

绘制图案

在前边的

$$x[n]=\{\begin{array}{r}100,n\in [1,24]\\ -500,n>25\end{array}$$

$$y[n]=\{\begin{array}{r}1.01y[n-1]+x[n],n\in [1,24]\\ 1.01(y[n-1]+x[n]),n>25\end{array}$$

假定月息为5%时，重新完成上述过程

在上述程序的基础上，我们只需要变更程序开始的Rate=0.05，即：

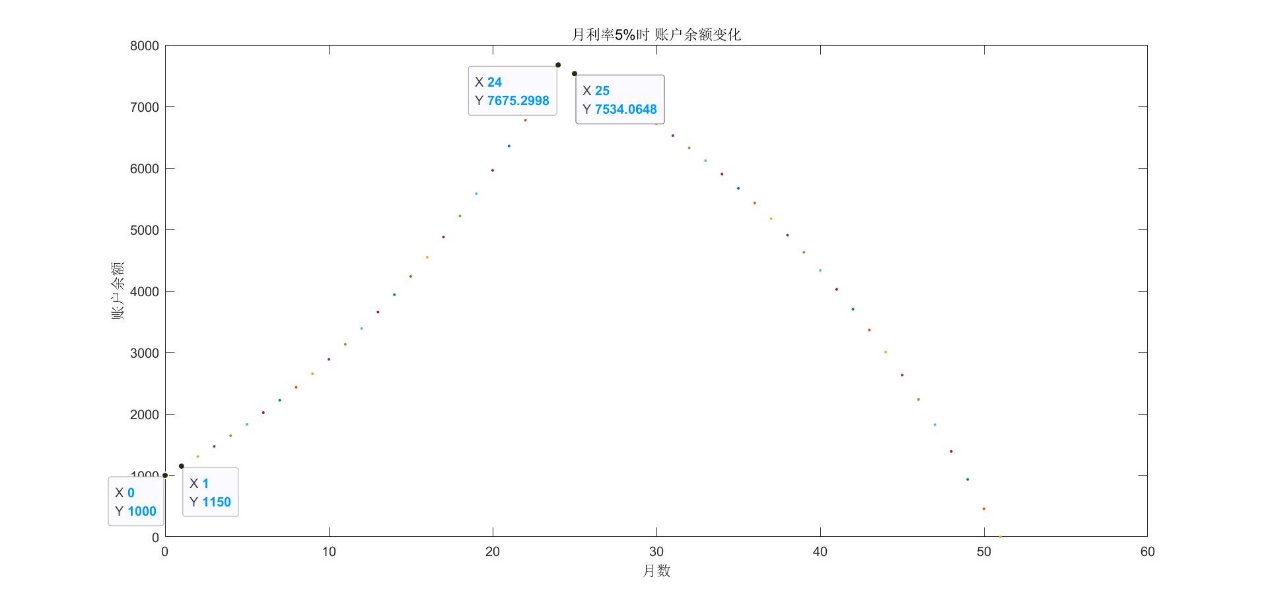
可以直观的看出，当51月的时候，账户余额为0。此外还可以对比两种情况：

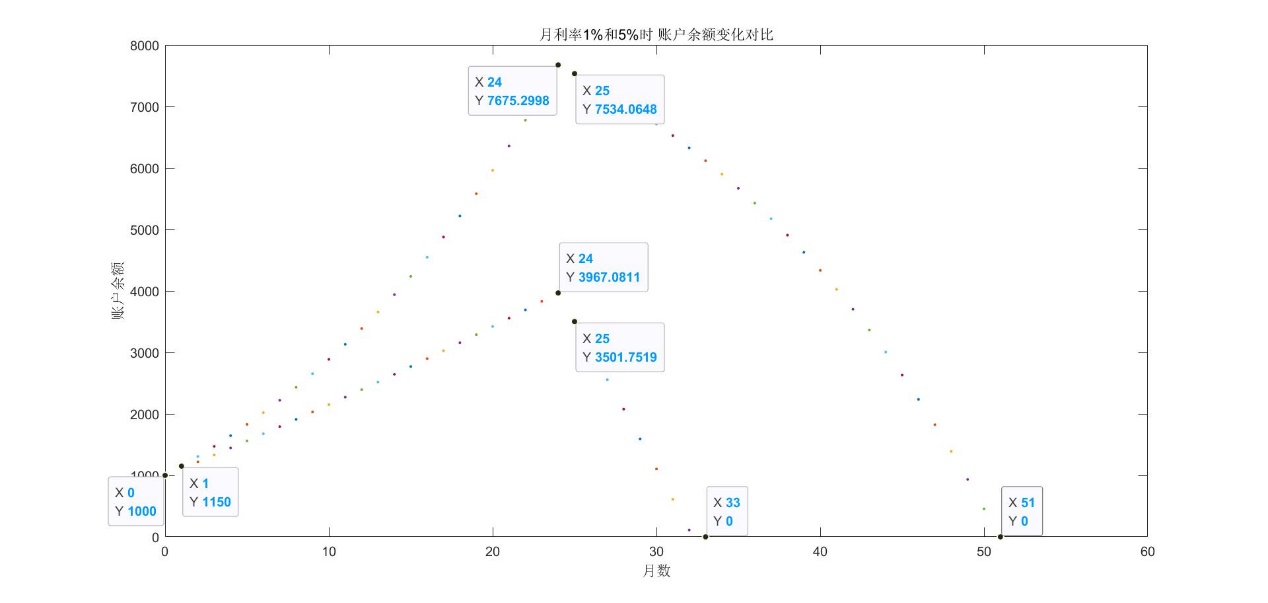
问题2------账户利益比最大设计

问题简述和分析

针对上述银行存款问题，假定银行存款月息为1%，仍以24个月为限。
要求：设计一个帐户存取款方案，使得帐户收益比最大。（帐户收益比＝取出资金总额/存入资金总额）

在这部分中，我们要考虑如何使得收益最大化。根据常识我们知道应当使得钱款尽可能早的存入账户，并且尽可能晚的取出账户。但我们仍然需要合理的证明来验证我们的思路。

蒙特卡罗模拟最大收益比

蒙特卡罗（Monte Carlo）方法，又称随机抽样或统计试验方法，针对某些问题，传统的经验方法由于不能逼近真实的物理过程，很难得到满意的结果，而蒙特卡罗方法通常采用随机数模拟的方法，能够真实地模拟实际物理过程，故解决问题与实际非常符合。^[2]

模型和假设

为了方便的解决问题，我们做出一些假设：

1. 每月只有存入或者取出；

2. 1月的时候账户初始金额为0；

3. 24月的时候不再存取，在月末取出所有的值。

在模型上我们仍然采用第一问的模型：

$$y[n]=\{\begin{array}{r}1.01y[n-1]+x[n],x[n]>0\\ 1.01\left(y[n-1]+x[n]\right),x[n]<0\end{array}$$

收益和存入金额的关系

首先考虑收益和每月存入的金额有无关系，由此我们有第二问的第一个程序：

syms y c q %设定 y c q分别是账户的余额 存入和取出 对应汉语拼音
syms x %总的金额是x
syms sum_c sum_q %总存入和总取出
syms scale %收益比
Rate=0.01;
y=0;%初始的y=0
sum_c=0;
sum_q=0;
flag=0;
c=rand*x;
y=y+rand*c;
sum_c=sum_c+c;
    for j=2:24
        c=rand*x;
        q=rand*x;
        sum_c=sum_c+c;
        sum_q=sum_q+q;
        y=(1+Rate)*(y-q)+c;
    end
    sum_q=sum_q+y;%更新取出的金额
    scale=vpa(sum_q/sum_c)

在这部分程序中，我们的金额是一个sym变量，我们通过这种方式来表示每月存取的金额是完全未知的，计算收益比scale发现，这是与x无关的一个变量，说明收益比和设置的初始金额是无关的。

蒙特卡洛模拟

收益比与设定的初始金额是无关的，于是在之前的基础上，我们修改初始金额为实数，方便我们进行比较和判断。

All=1000;  %定义金额
Rate=0.01; %定义月利率
Max_scale=0; %定义最大收益比
Real_time=0; %定义有效模拟次数
for i=1:10000000 %模拟次数
    y=0; %初始账户余额
    Sum_c=0; %总存入 每次开始模拟都清零
    Sum_q=0; %总取出 每次开始模拟都清零
    flag=0; %标记模拟是否有效
    first=rand*All; %第一个月只有存入 随机存入0-1000的值
    y=y+first;
    Sum_c=Sum_c+first;
    for j=2:24 %从第二个月开始
        x=(2*rand-1)*All; %随机产生存取金额 正的是存入 负的表示取出
        if y+x<0 %如果取金额大于账户余额 置flag为-1本次模拟无效
            flag=-1;
            break
        elseif x>0 %当存入的时候对应模型1.01y[n-1]+x[n]
            y=(1+Rate)*y+x;
            Sum_c=Sum_c+x;
        else %取出对应 1.01(y[n-1]+x[n])
            y=(1+Rate)*(y+x);
            Sum_q=Sum_q+abs(x);
        end
    end
    if flag==-1 %如果模拟无效 不做处理
        ;
    else %如果模拟有效
        Sum_q=Sum_q+y; %取出账户所有余额
        scale=vpa(Sum_q/Sum_c); %计算收益比
        if Max_scale<scale %更新收益比
            Max_scale=scale;
        end
    end
end
Max_scale %输出最大收益比
Real_time %输出有效模拟次数

在问题之初我们就根据常识做出假设，应当使尽早的存入账户，这种情况下的收益比应当是：

$$(1+0.01{)}^{23}=1.2571$$

通过数次模拟，我们得到的最大收益比都小于1.2571，所以我们可以根据蒙特卡洛模拟思想得出结论，最佳的存取模式应当是一次将所有的全部存入，然后在24月末的时候一次性取出。

总结

一个系统可以看成一个过程，在其中输入信号被该系统所变换，或者说系统以某种方式对信号做出响应。^[1]一个离散时间系统(discrete-time
system)就是将离散时间输人信号变换为离散时间输出信号:
$x[n]\to y[n]$

来自各种应用领域的系统，它们的数学描述往往具有惊人的共性。就像我们设置月利率为1%或者5%的时候，我们只需要简单的改变月利率的设置就可以将我们的模型变的通用。

很多在实践中很重要的系统都可以准确地建模，但是像我们在问题二中见到的系统，尽管我们的系统特性是确定的，我们也可以用一下的方式求得系统的单位脉冲响应。

但是在输入不确定的情况下，我们仍然不能确定系统响应的结果。并且系统也不是我们熟悉的LTI系统，给我们的分析带来了很大的困难，但是由于确定了系统的特性，我们仍然可以采用极限模拟的方式来得到我们想要的结果。也由此明白一个特性确定的系统才是有研究的价值的。

参考文献

1. 奥本海默.信号与系统[M].电子工业出版社:北京,2013:25.26

2. 沈海军.蒙特卡罗模拟[EB/OL].https://baike.baidu.com/item/%E8%92%99%E7%89%B9%E5%8D%A1%E7%BD%97%E6%A8%A1%E6%8B%9F/5160083?fr=aladdin,2020-10-29.