岭回归原理以及代码实现--机器学习

过拟合与欠拟合了解

在机器学习中模型的泛化能力很重要，泛化能力强的模型（本人理解为该模型对于大部分数据的拟合都能达到较好的效果即为泛化能力强的模型）是好模型。这里面就涉及到欠拟合与过拟合问题。

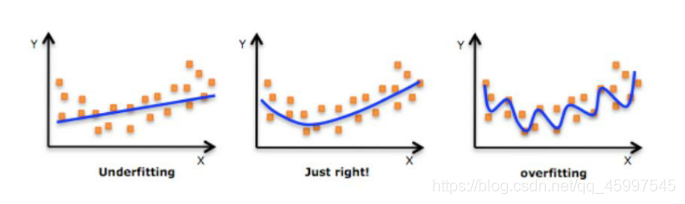
1.欠拟合underfitting：简单来说，就是用简单的模型去拟合复杂的数据，这会导致高Bias(偏差，即模型的期望输出与真实的输出之间的差异)
2.过拟合overfitting：用复杂的模型去拟合简单的数据，会导致高Variance(方差，刻画了不同的训练集得到的模型的输出与这些模型期望输出的差异)

用图可能更好理解一些，依次为欠拟合，拟合效果好，和过拟合。

想解决欠拟合，就要添加多项式特征，或者添加其他特征减少正则化参数。
而想改善或解决过拟合，最好的办法就是正则化，即保留所有的特征，减少参数的大小。

正则化与岭回归

岭回归就是在损失函数中加入正则化，（正则化就是所有参数$\theta$的平方和，也就是l2范数，其中算平方和的时候不包括${\theta }_0$）改变了梯度下降法中的$\theta$更新公式，用正则化改善or减少模型的过拟合问题，用一个例子来理解：

我们知道线性回归的损失函数为：$J_{\theta }=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i{)}^2$

而岭回归的损失函数是线性回归的损失函数加正则化：
$J_{\theta }=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i{)}^2+\lambda \sum _{j=1}^x{\theta }_j^2$

$\lambda$就是正则化的参数，该值选取过大，会把所有的$\theta$参数都最小化，造成欠拟合。选取过小，会解决不了过拟合问题。

知道以上所说的含义之后，现在给出一个式子：
$mi{n}_{\theta }=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^i)-y^i{)}^2+1000{\theta }_3^2+10000{\theta }_4^2$
在这个式子中我们设定的$\lambda$值一个为1000，一个10000，很大了对吧？现在呐，这个式子要求最小值，要咋办呐，在$\lambda$值给定很大的情况下，我们只能让参数$\theta$值减少到最小，这样才保证最终的结果最小。这个过程就是上面所说的，解决过拟合就是添加正则化（即保留所有特征，减少参数大小）

了解以上原理之后，再来看下面的多项式，
$h_{\theta }={\theta }_0+{\theta }_{1}x+{\theta }_2{x}^2+{\theta }_3{x}^3+{\theta }_4{x}^4$
根据以上分析，该公式想要求得最优解（逼近至最小值）就可使用梯度下降法进行迭代逼近。而梯度下降法中的代价函数（损失函数）部分即为岭回归的损失函数。
由于岭回归是加入正则化的损失函数（减少了参数大小），所以梯度下降法中的$\theta$更新公式也加入了正则化，推导结果如下：
${\theta }_j=(1-\frac{\alpha \lambda }{m}){\theta }_j-\frac{\alpha }{m}\sum _{i=1}^m((h_{\theta }(x^i)-y^i)x_j^i$
把上面的更新公式向量化之后就可以转成代码进行岭回归实现了。

（$\theta$更新公式推导敲出来太麻烦了，感兴趣的盆友可以私我发手推笔记）

岭回归代码实现

#代码规范化，用函数包装成代码块，不要散着写
#岭回归代码，只有theta更新公式不一样，加了正则化
import numpy as np
import matplotlib.pyplot as plt
from sklearn.metrics import mean_absolute_error,mean_squared_error,median_absolute_error,r2_score

#1.首先读取数据，写一个读取数据的函数
def getData():
    data=np.loadtxt("F:/comdata/aqi2.csv",delimiter=',',skiprows=1,dtype=np.float32)
    X=data[:,1:]  #二维矩阵
    Y=data[:,0]  #打印结果为一行
    Y=Y.reshape(-1,1) #将y的一行转为一列二维矩阵，行数由列数自动计算
    X=dataNumalize(X) #归一化之后的X
    return X,Y

#2.将特征集数据进行归一化处理，处理后的数据也是要进行输出，所以此函数要在读取数据的函数中进行调用
#归一化是对一个矩阵进行归一化，所以此函数有一个参数
#归一化使用（某个值-均值）/标准差
def dataNumalize(X):
    mu=X.mean(0)  #对X特征集的第一列的均值 X(n)
    std=np.std(X)  #S(n)
    X=(X-mu)/std   #将归一化处理结果赋值X
    index=np.ones((len(X),1)) #最后一列1
    X=np.hstack((X,index)) #进行合并 ，此合并函数只含一个参数，所以将X，index带个括号看成一个参数
    return X

#3.下面计算损失函数，在损失函数中有3个参数：theta,X,Y
def lossFuncation(X,Y,theta):
    m=X.shape[0]  #m是X特征集的样本数，即行数
    loss=sum((np.dot(X,theta)-Y)**2)/(2*m)
    return loss

#4.下面实现批量下降梯度算法
#此算法的theta更新公式中有四个参数，X,Y,theta,alpha
#另外我们需要定义一个迭代次数num_iters，就是更新多少次（alpha走多少步）才能下降到最低点，每迭代一次，theta就更新一次
def BGD(X,Y,theta,alpha,lamba,num_iters):
    m=X.shape[0]
    loss_all=[]  #定义loss值列表，把每次theta更新时跟着变动的loss函数值存入展示
    for i in range(num_iters):
    #参数的更新公式向量化如下两行代码
        theta=theta-alpha*np.dot(X.T,np.dot(X,theta)-Y)/m
        theta[:-1]=theta[:-1]-alpha*(lamba/m)*theta[:-1]
        loss=lossFuncation(X,Y,theta)
        loss_all.append(loss)  #吧loss值添加到loss_all列表中去
        print("第{}次的loss值为{}".format((i+1),loss))
    return theta,loss_all

#5.主函数进行测试
#此测试没有区分text和predict，所有的数据用来做测试集
if __name__=='__main__':
    X,Y=getData()
    theta=np.ones((X.shape[1],1))  #对theta起点值进行初始化
    num_iters=1000  #初始化迭代次数为500
    alpha=0.01  #初始化α（下降步长）为0.01
    lamba=0.05#参数lambda
    theta,loss_all=BGD(X,Y,theta,alpha,lamba,num_iters) #调用BGD函数求theta更新参数，和每次更新后的loss函数值
    print(theta)
    #做模型预测
    y_predict=np.dot(X,theta)



#最后进行一个模型的评价----根据模型评价指标与所的结果进行判定,结果与迭代次数有关
print("平均绝对误差：",mean_absolute_error(Y,y_predict))
print("均方误差：",mean_squared_error(Y,y_predict))
print("中之绝对误差：",median_absolute_error(Y,y_predict))
print('r2',r2_score(Y,y_predict))

#模型测试完毕，模型预测结果进行数据可视化
plt.scatter(np.arange(100),Y[:100],c='red')  #真实label
plt.scatter(np.arange(100),y_predict[:100],c='green') #预测的label
plt.show()
#绘制损失函数随着迭代次数改变所进行变化曲线
plt.plot(np.arange(num_iters),loss_all,c='black')
#plt.show()

运行结果如下：