【价格型需求响应】基于Logistic函数的负荷转移率模型需求响应研究（Matlab代码实现）

最新推荐文章于 2025-04-30 16:33:46 发布

科研_G.E.M.

最新推荐文章于 2025-04-30 16:33:46 发布

阅读量823

点赞数 27

文章标签： matlab 人工智能机器学习

本文链接：https://blog.csdn.net/qq_46009436/article/details/147546726

版权

👨‍🎓个人主页

💥💥💞💞欢迎来到本博客❤️❤️💥💥

🏆博主优势：🌞🌞🌞博客内容尽量做到思维缜密，逻辑清晰，为了方便读者。

⛳️座右铭：行百里者，半于九十。

📋📋📋本文目录如下：🎁🎁🎁

目录

💥1 概述

基于Logistic函数的负荷转移率模型在价格型需求响应中的研究

负荷转移率模型

一、价格型需求响应的核心机制

二、Logistic函数在需求响应建模中的优势

三、基于Logistic函数的负荷转移率模型框架

1. 模型结构

2. 关键参数与确定方法

四、模型应用案例与验证方法

1. 实际应用案例

2. 模型验证方法

五、模型优势与局限性

优势：

局限性：

六、未来研究方向

总结

📚2 运行结果

🎉3 参考文献

🌈4 Matlab代码实现

💥1 概述

基于Logistic函数的负荷转移率模型在价格型需求响应中的研究

从需求侧角度看，随着电力市场的不断完善，交易主体的多元化，交易方式的透明化以及交易内容的灵活化，为需求侧响应的发展注入了新的活力[11-12]。根据“十三五”时期经济社会发展理念，电力需求侧管理（Demand Side Management，DSM）工作要求积极推广需求响应，持续引导节约用电，促进智能用电升级，推动电力供需协同互动。在这一背景下，需求响应（Demand Response，DR）技术作为一种新型的管理措施在我国重点城市进行初步试点工作，利用电网侧价格信号或激励信号积极引导用户优化用电方式，提高用电效率，从而使得电网整体负荷形态有所改善，电力供需矛盾有所缓解，促进电力系统高效稳定运行[13-14]。此外，需求响应技术还有利于缓解新能源的随机波动性给电力系统带来的负面影响，为电力系统的安全性提供保障。因此，需求响应技术的应用对能源经济发展、电力工业以及环境环保等方面具有重要的战略意义[15]。

负荷转移率模型

由消费者心理学可知，电价差过大、过小以及在电价变化处响应度曲线的平滑，均会引起用户需求

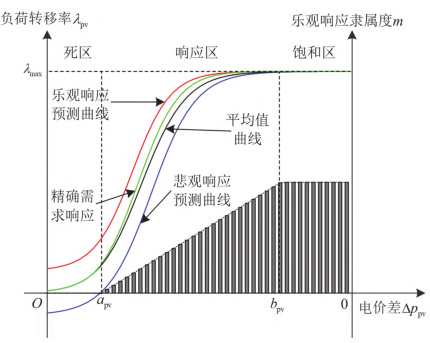
响应的变化。在电价激励机制下，用户本着自愿原则，其响应行为具有明显的随机性，则真实的需求响应曲线会处于乐观与悲观响应预测曲线之间，具备模糊属性［17］。本文以峰谷负荷转移为例，建立了基于 Logistic函数的模糊响应机理模型，如图 1 所示。图中，λpv为负荷转移率；m为乐观响应隶属度，表示用户符合乐观响应估计的概率；Δppv为电价差；apv和bpv为电价差划分区域分界点；柱形图所围成的梯形部分为采用偏大型半梯形隶属度函数反映不同电价差下对应的乐观响应隶属度 m；曲线部分为在不同电价差下，不同响应曲线对应的峰转谷负荷转移率λpv。该模型划分了死区、响应区和饱和区。在死区，电价差过小，用户响应行为具有很强的随机性，故由

乐观和悲观响应预测的平均值确定。在响应区，随着电价差增大，用户响应积极性被调动，且响应行为更倾向于乐观响应曲线。因此需考虑乐观响应隶属度，并将其作为需求响应机理的概率约束，采用偏大型半梯形隶属度函数计算。在饱和区，2 条曲线重合，用户响应行为即可用负荷转移率最大值表示。

Logistic函数利用可变参数，增加负荷转移率变化的跨度，其函数模型如式（1）所示。响应区为表征用户更趋向于乐观响应曲线的行为特征，采用不同电价差对应的乐观响应隶属度作为概率约束，则综合负荷转移率如式（2）和式（3）所示：

一、价格型需求响应的核心机制

价格型需求响应（Price-Based Demand Response, PBP）通过电价信号引导用户调整用电行为，主要包含分时电价（TOU）、实时电价（RTP）和尖峰电价（CPP）三种机制。其核心目标是通过电价差（如峰谷价差）激励用户将高峰负荷转移至低谷时段，实现“削峰填谷”效果。例如，分时电价将24小时划分为峰、平、谷三个时段，分别对应高、中、低电价，直接反映不同时段的供电成本差异。

二、Logistic函数在需求响应建模中的优势

Logistic函数因其S型曲线特性，能够有效描述用户响应行为的非线性特征，包括：

饱和效应：当电价差超过某一阈值时，用户响应趋于稳定（饱和区）。
模糊属性：用户响应介于乐观（最大转移率）与悲观（最小转移率）预测之间，需通过隶属度函数量化。
动态适应性：通过参数调整（如斜率、中心点）可适应不同电价策略下的响应跨度。

三、基于Logistic函数的负荷转移率模型框架

1. 模型结构

分区定义：根据电价差（Δppv）将用户响应划分为三个区域：
- 死区（Δppv ≤ apv）：电价差过小，用户响应随机性强，负荷转移率接近零。
- 响应区（apv < Δppv ≤ bpv）：用户响应积极性随电价差增加而显著提升，Logistic函数主导非线性变化。
- 饱和区（Δppv > bpv）：用户弹性潜力耗尽，转移率达到最大值。
数学表达式：
- 乐观转移率：λmax=al1+e−(Δp−cl)/ul+blλmax=1+e−(Δp−cl)/ulal+bl
- 悲观转移率：λmin=ab1+e−(Δp−cb)/ub+bbλmin=1+e−(Δp−cb)/ubab+bb
- 综合转移率：结合乐观隶属度m=(Δp−apv)/(bpv−apv)m=(Δp−apv)/(bpv−apv)，加权计算最终值。

2. 关键参数与确定方法

电价差阈值（apv, bpv） ：通过历史数据分析或实验标定，划分响应区域。
Logistic参数（a, b, c, u）：
- 使用历史负荷与电价数据，采用最大似然估计或非线性最小二乘法拟合。
- 例如，参数c反映响应区中点，调整后可使曲线更贴合实际数据。
隶属度函数：采用偏大型半梯形函数量化用户对乐观响应的倾向性。

四、模型应用案例与验证方法

1. 实际应用案例

微电网优化调度：在含CCHP型微网的配电网中，通过Logistic模型调整负荷转移率，实现能源平衡。例如，杨世博等人的研究中，模型使峰谷差降低15%-20%。
综合能源系统：在区域综合能源系统中，结合电、热负荷转移模型，优化调度策略降低运行成本。

2. 模型验证方法

仿真对比：与传统模型（如弹性矩阵、线性分段模型）对比负荷曲线拟合度。例如，葛晓琳等通过对比四类模型，验证Logistic模型在平滑负荷波动方面的优势。
数据驱动验证：
- 历史数据回测：利用智能电表数据验证转移率预测精度。
- 模糊机会约束规划：将不确定性建模为模糊变量，通过清晰等价处理转化为确定性优化问题。
参数敏感性分析：测试关键参数（如apv、斜率k）对模型输出的影响，评估鲁棒性。