文章目录
一、贝叶斯决策论
1.1 简介
我们可能都知道贝叶斯决策论(ayes Decision Rule),虽然我们可能能背诵出来,但我们要对他正确理解却不容易。
在这里我们需要知道的是:
- 什么是贝叶斯决策论,为什么说它是最优化的?
1.2 简单认识
通常在机器学习的时候我们一般通过观测数据 X 来推断 Y。在这个过程中我们学习我们的推算的过程,使得我们后面进行估计的时候我们的推算过程是对于正确的结果最优的。举个例子,我们有一个硬币,我们观察到了他的尺寸大小是多少,我们就可以通过一个规则(运算或推算过程)来计算我们的投出后的结果是什么。在这里我们可以得到,我们得到的数据是:硬币的大小 X,结果(0,1),运算过程。
1.3 当我们啥也不知道的时候咋办
当我们什么都不知道的时候,按照我们正常的思维我们的概率都是五五开。巧了,这时候一个人托梦告诉你正面的结果是0.8,这时候我们就得到了反面的概率 1-0.8=0.2 。对于他们的概率结果分布的不一样,我们的结果更加趋向概率高的那一个,这时候我们可以计算出来我们出错的概率是0.2。
在上面我们计算出来的我们称之为先验概率(prior probability)就是说的是我们通过观测得到的已知的概率分布,在后面的推算中,我们可以不用去管他的大小,我们直接大胆的推测,在后面我们会介绍后验概率posterior probability)
后验概率指的是我们通过观测对结果的估计。(前面的啥也不知道的时候我们是没有进行观测的,我们把结果交给了一个叫神的家伙)。
1.4 当我们得到观测的数据咋个整呢
在前面的计算中我们只是把我们的结果交给了神,这是不科学的,我们在这里要引入科学的办法。在这里我们得到了硬币的尺寸 X ,然后我们就可以估计我们的概率咯,在这里我们引入数学的表达就是估计
。相反的我们的
就是表达的我们的结果是反的概率,在这里我们可以理解为我们代表当我们观测到硬币属性 X 时概率正为1,反之为0。我们在这里给这两个数学表达式起个名字,就是我们先前提出的后验概率,和我们直接估计的结果0和1是不一样的,这个是我们计算仅当*X*被观测到时y=1的概率。
到了这里,大家都应该有了自己的理解,先验概率就是对结果直接进行估计,我们的后验概率就是对结果加入观测量使他更加的准确,就是对原有的计算概率方式的一种更新,使得它更加的优化,更加的完美。这就是所谓的相信科学。
后验概率对于机器学习来讲是最好的,也是大部分的学习模型希望得到的。
1.5 贝叶斯公式
后验概率我们是没办法直接得到的,因此我们需要找到方法来计算,这里我们就引入了贝叶斯公式。后验概率的表达方法我们称之为条件概率(conditional probability)一般写作p(a|b),即仅当事件B发生的时候A发生的概率,假设两种概率(A 或 B)都大于零,我们得到:
化简得到:
化简得到:
我们可以通过我们的观察发现概率
和
是等价的,所以他们的右边也是等价的,我们得到
。于是我们就得到了贝叶斯公式:
,将它带入我们上面提到的后验概率中去就有了:
公式1:正面朝上的后验概率------>
公式2:反面朝上的后验概率------>
**我们发现,在通过贝叶斯公式变形后,后验概率变得可以计算了。**观察公式1和2的等号右边,发现这些概率都可以通过观测获得。
贝叶斯决策的预测值是选取后验概率最大的结果。
1.6 如何决策最优
因为
,也就是“观测到X并预测为反面的错误概率“就是“观测到X并预测为正面的后验概率”。
因此只要观测到X,并选择后验概率最大的结果,就可以最小化预测的错误概率。这个结论对所有观测值X均成立,因此只要按照这个预测逻辑,那么就可以保证预测的错误概率最小化,所以才叫做“最优”。
二、朴素贝叶斯分类器
在我们的生活中,很多时候我们都会用到分类,比如在你旁边走过了一个人,你会判断他是不是学生还是精神小伙,这一类的东西就是对生活中的东西进行分类。然后我们还有一种分类方法我们称之为朴素贝叶斯分类器,也是我们分类过程中的一种分类方法。
2.1 概述
在数学的角度中,分类问题可做如下定义:已知集合 C=y1,y2,y3,y4…和 I=x1,x2,x3,x4…,确定映射规则y = f(x),使得任意 Xi属于I有且仅有一个 ,使得 Yi属于F(Xi)成立。
我们称之为c为我们的类别,对应每一个x;而众多的x构成的 I 我们称之为特征集合,其中每一个元素都是一个待分类项,f是分类器。分类算法的目的是来构造这个F。
我们都知道分类算法就是特征值到类别的映射关系,所以我们要做的就是找到这一层的关系。
2.2 贝叶斯分类器
在我们的第一个部分中我们得到了我们的贝叶斯公式:
我们换一种表现形式就是:
我们只要计算出了 p 我们的工作就完成了。
2.3 例题解析
我们首先给出我们的数据:
我们的问题是讨论我们用贝叶斯方法,看能不能计算出来女生嫁不嫁这个男生的概率,在这里我们给出一个数学问题的表示方法:p(嫁|(不帅、性格不好、身高矮、不上进))与p(不嫁|(不帅、性格不好、身高矮、不上进))的概率,谁的概率大我们的结果就是什么。
我们联系我们的贝叶斯方程式:
那么我只要求得p(不帅、性格不好、身高矮、不上进|嫁)、p(不帅、性格不好、身高矮、不上进)、p(嫁)即可,好的,下面我分别求出这几个概率,最后一比,就得到最终结果。
p(不帅、性格不好、身高矮、不上进|嫁) = p(不帅|嫁)*p(性格不好|嫁)*p(身高矮|嫁)*p(不上进|嫁),那么我就要分别统计后面几个概率,也就得到了左边的概率!
在这里我们需要注意的是,我们的等式成立的条件需要特征之间相互独立。
2.4 何为朴素
为什么会有朴素贝叶斯分类器的朴素这两个字呢,朴素贝叶斯算法是假设各个特征之间相互独立,那么我们就可以解释了,为什么我们的等式可以成立。
2.5 为什么需要特征之间的相互独立呢?
就像我们例子中的一样,我们的例子中有四个特征,其中就是帅不帅,性格如何,升高,是不是上进,那么如果我们四个特征之间各自分类类别相乘我们得到一个四维的空间,总个数就会变得多了起来。在我们的象是生活中我们往往有特别多的特征,比如你估计一个人的家庭生活水平,你要了解到他的服饰牌子,消费水准,常去什么地方,生活费用一些,我们会有大量的特征,如果通过统计来估计后面概率的值,这就显示了不独立的弊端,所以这也是为什么我们要假设他是独立的原因。
2.6 总结
*朴素贝叶斯法对条件概率分布做了条件独立性的假设,由于这是一个较强的假设,朴素贝叶斯也由此得名!这一假设使得朴素贝叶斯法变得简单,但有时会牺牲一定的分类准确率。*
三、半朴素贝叶斯分类器
3.1 概述
在朴素贝叶斯的问题上,我们知道了他的特征属性是存在“独立性”的,也就是属性条件独立性的设想,那么我们就会存在一个问题,如果我们的属性之间有依赖呢,那如果这样想的话我们就不难看出我们的贝叶斯算法”草率了“,那么随着这种构想的提出,所以半朴素贝叶斯算法就出现了,他们之间的区别是对于假设独立特征之间的绝对独立性的一种放松,体现在适当的考虑一部分的依赖关系。
3.2 核心思想
半朴素贝叶斯算法的核心思想是考虑一部分的依赖关系,独依赖估计(One-Dependent Estimator,简称ODE)是半朴素贝叶斯分类器最常用的一种策略。也就是我们说的考虑一部分的依赖关系。
独依赖估计:每个其他属性最多只依赖一个属性,即:
3.3 基本构造
对于父属性已知的计算,可采用式子9的计算方式进行计算。我们的问题在于如何确认父属性,最简单的方式是如果 b 所示,SPODE,称为超父属性,X1为超父属性。
TAN树则是在最大带权生成树算法的基础上,通过一下步骤获得(c)的树形结构:
(1) 计算任意两个属性之间的条件互信息
2) 以属性为节点构造完全图,两节点之间的权值为互信息,即:
(3) 构建此完全图的最大带权生成树,挑选根变量,将边设置为有向的;
(4) 加入类别节点y,增加从y到每个属性xi的有向边;
通过条件互信息就刻画了属性之间的依赖关系,然后基于互信息计算属性之间的权值,从而实现半朴素贝叶斯网络的构建。
AODE是一种基于集成学习的方法、更为强大的独依赖分类器为基础进行构造。与SPODE确定超父属性的方法有一点的不同,AODE尝试将每个属性都作为超父属性来构建SPODE,然后将具有足够训练支撑的SPODE集成起来作为最终结果,即:
四、贝叶斯网
4.1 概述
简单来说,贝叶斯网络就是将某一个研究系统按照设计的随机变量,感觉不是或者是的条件独立都绘制在一个有向图。
贝叶斯网络是一个有向无环图,是一种概率图模型,根据概率图拓扑结构,考察随机变量{x1x2,x3…xn},也就是它N组的条件概率的分布性质。
其中有向无环图的节点表示的是随机变量,两个节点之间的连接箭头就是表示之间的因果关系,所以这两个节点就构成一个条件概率,也就是他们之间的映射组成一个整体。
4.2 实例
这是一个简单的贝叶斯网络:
P(a,b,c)=P(c|b,a)P(b|a)P(a)
我们通过他们之间的箭头可以看见a是b和c的因,b是c的因,a有两个果b和c,c同时也是b的果,所以我们可以通过他们连接线的方向来判断他们之间的相互关系(通过推导)。
但是我们需要注意的是,在我们的贝叶斯中有的随机变量会出现缺失,也就是没有因或者没有果,这是正常的现象。
在我们的这个图中,我们可以直接看出来我们的x1和x2还有x3独立,x6,x7在条件的约束下独立,我们也可以直接看出来整个组的随机变量的全分布:P(x4|x1x2x3)P(x5|x1x3)P(x6|x4)P(x7|x4,x5)P(x1)P(x2)P(x3)
4.3 分析
对于一个实际的贝叶斯网络的分析如下:
我们的分析首先看的是CPD图,在这个图里面我们可以看出来D以来的是c和b,在这个概率分布中我们看出来当c和b不发生的时候,不是呼吸困难的概率是0.9,得了的概率是0.1;当c发生b不发生的时候,是呼吸困难的概率是0.3,不是的概率是0.7…以此类推,我们也就明白了贝叶斯图所表达的是什么意思。
<br
4.4 特殊贝叶斯
看出,此处节点形成一条链式网络,这有个很著名的名称叫做马尔科夫模型.即其中Ai+1只和Ai有关。
五、EM算法
5.1 EM简介
EM算法是一种迭代的算法,用于含隐变量(latent Variable)求概率模型参数的极大估似然估计,或极大后验概率估计EM算法由两个步骤组成,求期望的E步和求极大的M步。
EM算法可以看作是一种特殊情况下的极大似然的一种算法,因为在处理数据的时候有可能我们们的数据会出现缺失数据,含有隐变量等问题,当我们遇到这种问题,计算极大似然函数通常是比较复杂的,这时候我们的em算法恰好能解决这个问题。
5.2 极大似然估计
它可以理解为极大似然原理上的统计犯法,在这里有可能大家对极大似然估计不太明白,我这里说明原理,我们有一组数据,我们对他进行计算的结果可能有x1,x2,x3,x4…等等,但是再一次计算的过程中,我们发现我们计算的结果中出现了x3,那么我们就认为我们的实验条件对于x3这个结果是比较好的,也就是因为x3作为结果的概率比较大。
举个例子:
我们设甲箱中有99个白球,1个黑球;乙箱中有1个白球.99个黑球。现随机取出一箱,再从抽取的一箱中随机取出一球,结果是黑球,这一黑球从乙箱抽取的概率比从甲箱抽取的概率大得多,这时我们自然更多地相信这个黑球是取自乙箱的。一般说来,事件A发生的概率与某一未知参数θ有关,θ 取值不同,则事件A发生的概率
也不同,当我们在一次试验中事件A发生了,则认为此时的θ 值应是t的一切可能取值中使
达到最大的那一个,极大似然估计法就是要选取这样的t值作为参数t的估计值,使所选取的样本在被选的总体中出现的可能性为最大。
5.3 jensen不等式
5.3.1 定义
设f是定义域为实数的函数,如果对于所有的实数X,f(x)的二次导数大于等于零,那么f是凸函数。Jensen不等式表述如下:如果f是凸函数,x是随机变量,那么:E[f(X)]>=f(E[X]) 。当且仅当X是常量时,上式取等号。
5.3.2 eg
图中,实线f是凸函数,X是随机变量,有0.5的概率是a,有0.5的概率是b。X的期望值就是a和b的中值了,图中可以看到E[f(X)]>=f(E[X])成立。 Jensen不等式应用于凹函数时,不等号方向反向。
5.4 算法推导
具体的计算过程如下:
固定好了Q(z),再去调整参数 Θ ,使得下界最大。
个人学习,借鉴如下文献,在这里对原作者感到感谢。
致谢:https://www.zhihu.com/question/27670909
致谢:https://www.zhihu.com/question/20138060
致谢:https://blog.csdn.net/cxjoker/article/details/81878037
致谢:https://blog.csdn.net/weixin_41575207/article/details/82077800
致谢:https://baike.baidu.com/item/极大似然估计/3350286?fr=aladdin
致谢:https://blog.csdn.net/qq_39521554/article/details/79248993
致谢:https://www.cnblogs.com/vincentbnu/p/9503284.html








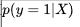
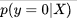
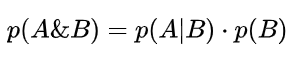
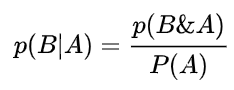


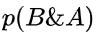
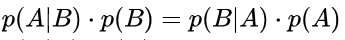
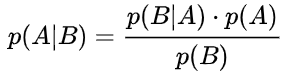
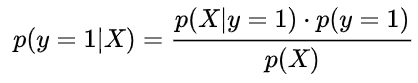
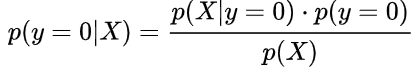
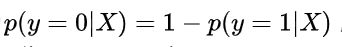









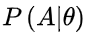
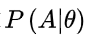














 1183
1183











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








