三个弹簧振子理论

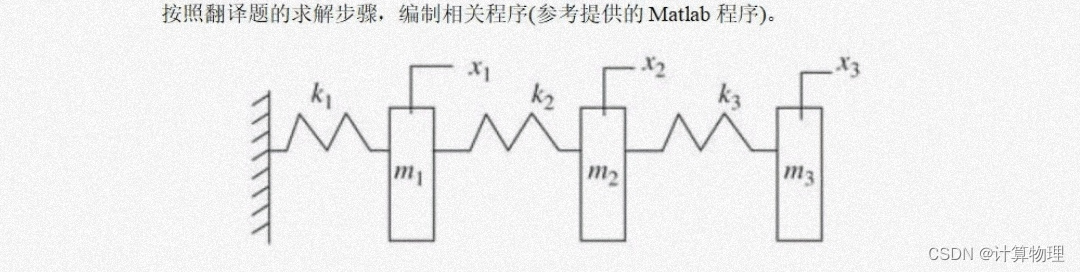
三个弹簧振子理论建立如图 １ 所示的一维三弹簧振子的实验系 统:三个弹簧振子的质量均为ｍ1,m2,m3，弹簧的劲度系 数分别为k1,k2和k3 ，三个谐振子在微振动过程 中相对自身的平衡位置的位移分别为x1、x2 和 x3 ，取x1、x2 和 x3 广义坐标，则系统的动力学方程可表示为:

 

• 代码

弹簧摆摆动图

clc;clear;

global k1 k2 k3 M1 M2 M3

k1=145000;

k2=180000;

k3=121000;

M1=220;

M2=240;

M3=350;

t1=[0,5];H1=[4;0;8;0;12;0];

[t,H] = ode45(@dH,t1,H1);%求解动力学方程

figure('numbertitle','off','name','弹簧摆摆动图');

subplot(1,2,1);

plot(t,H(:,1),'b','linestyle','-','LineWidth',1.5);hold on;

plot(t,H(:,3),'r','linestyle','-','LineWidth',1.5);hold on;

plot(t,H(:,5),'g','linestyle','-','LineWidth',1.5);hold on;

legend('x1位置关系','x2位置关系','x3位置关系');axis([0 2.5 -13 13]);

set(gca,'linewidth',2); title('位置变化曲线');

xlabel('时间');ylabel('位置');box on;grid on;

subplot(1,2,2);

plot(t,H(:,2),'b','linestyle','-','LineWidth',1.5);hold on;

plot(t,H(:,4),'r','linestyle','-','LineWidth',1.5);hold on;

plot(t,H(:,6),'g','linestyle','-','LineWidth',1.5);hold on;

legend('x1速度关系','x2速度关系','x3速度关系');axis([0 2.5 -110 110]);

set(gca,'linewidth',2); title('速度变化曲线');

xlabel('时间');ylabel('速度');box on;grid on;

function dHdt=dH(t,H)

global k1 k2 k3 M1 M2 M3

dHdt=zeros(6,1);

dHdt(1)=H(2);

dHdt(2)=-k1*H(1)/M1+k2*(H(3)-H(1))/M1;

dHdt(3)=H(4);

dHdt(4)=-k2*(H(3)-H(1))/M2+k3*(H(5)-H(3))/M2;

dHdt(5)=H(6);

dHdt(6)=k3*(H(3)-H(5))/M3;

end

 弹簧动图

clc;clear;

global k1 k2 k3 M1 M2 M3

k1=145000;

k2=180000;

k3=121000;

M1=220;

M2=240;

M3=350;

t1=[0,5];H1=[4;0;8;0;12;0];

[t,H] = ode45(@dH,t1,H1);%求解动力学方程

figure('numbertitle','off','name','弹簧轨迹图');

R=0.3;

 

xx1=20;xx2=40;xx3=60;

for i=1:10:length(t);

clf;hold on;

gg1=0:0.1:xx1+H(i,1);yy1=0.15+0.02*sin(gg1);

plot(gg1,yy1,'LineWidth',3,'Color','b');hold on;%第一个弹簧

gg2=xx1+H(i,1):0.1:xx2+H(i,3);yy2=0.15+0.02*sin(gg2);

plot(gg2,yy2,'LineWidth',3,'Color','r');hold on;%第二个弹簧

gg3=xx2+H(i,3):0.1:xx3+H(i,5);yy3=0.15+0.02*sin(gg3);

plot(gg3,yy3,'LineWidth',3,'Color','g');hold on;%第三个弹簧

plot([xx1+H(i,1),xx1+H(i,1)],[0,R],'LineWidth',16,'Color','b');hold on;%第一个物体

plot([xx2+H(i,3),xx2+H(i,3)],[0,R],'LineWidth',16,'Color','r');hold on;%第二个物体

plot([xx3+H(i,5),xx3+H(i,5)],[0,R],'LineWidth',16,'Color','g');hold on;%第三个物体

line([0,0],[0,0.3],'color','k','linewidth',2);hold on;

line([0,100],[0 0],'color','k','linewidth',2);hold on;

xlabel('x');ylabel('y');box on;

hold off;set(gca,'Visible','off');%设置边框宽度

axis([0 100 0 0.8]);

pause(0.5);%加坐标边框%加网格线%可以在这里添加输出动图的程序

drawnow;%实时更新坐标图窗口

end

 

function dHdt=dH(t,H)

global k1 k2 k3 M1 M2 M3

dHdt=zeros(6,1);

dHdt(1)=H(2);

dHdt(2)=-k1*H(1)/M1+k2*(H(3)-H(1))/M1;

dHdt(3)=H(4);

dHdt(4)=-k2*(H(3)-H(1))/M2+k3*(H(5)-H(3))/M2;

dHdt(5)=H(6);

dHdt(6)=k3*(H(3)-H(5))/M3;

end