遗传算法中的模式定理

一、模式基本定义 (schema)

\quad\quad 遗传算法的进化种群一般是多个个体来表示，这些个体常常是用一些串来表示，这些串被称为基因串。每个基因串是由多个基因（字符) 组成的，每个基因可以用字母或数字表示。如果是二进制编码的遗传算法，每个基因可用数字 0，1 来表示，那么每个个体就是由 0 和 1 组成的串。这也是最简单和最常用的编码方式，当然也有其他编码方式，如整数编码，实数编码。如果多个基因串具有相同的性质，例如，用英文字母构成的基因串 ABEFA 和 ABCEF ，这两个串在第一和第二个位置都是 ‘A' 和 ‘B'。把所有具有这样特点的串的集合用串 AB*** 来表示，其中 * 就是不确定字符，它可取 {A,…,Z} 中任何一个字符。那么这些具有相同性质的串的集合就可以用一个带有不确定字符的串来表示，这就是模式(schema)。模式是 Holland 在 1975 年提出的，这些串的长度大多数是固定不变的。比如，如果基因串有 L 个字符组成，而每个字符有 C 个可能取值，那么一共有 C^L 个可能基因串 (个体)。下面列出二进制编码遗传算法的一些基本概念：

\quad\quad 定义 1.1 通配符 (Non-Defining Allele)

\quad\quad 在一个由 {0, 1, *} 中字符构成的字符串中，字符 * 叫做通配符，它不是确定字符，可表示 0 或 1，而字符 0 和 1 均称为确定字符。确定字符所在的位置称为确定位，相应地，不确定字符 * 所在的位置称为不确定位。

\quad\quad 定义 1.2 模式 (Schema)

\quad\quad 一个由 {0, 1, *} 中字符构成的字符串称为一个模式，它表示将其中每个* 都用 0 或 1 任意替换后所得的所有可能的字符串集合，记做 H。例如，H = 01**1={01001,01011,01101,01111}，值得注意的是，如果字符串中没有不确定字符 *，它也是一个模式。例如 H=01011 也是模式(其本身)。

\quad\quad 定义 1.3 模式的阶 (Schema Order)

\quad\quad 模式 H 中确定字符的个数称为模式的阶，记做 O(H)，若 O(H) = k，该模式记为 H_k 。例如，对 H=01**1，其模式阶为 O(H)=3，该模式 H 也可记做 H₃.

\quad\quad 定义 1.4 串长 (String Length)

\quad\quad 模式 H 中所有字符的数量为 l，则称该模式的串长记为 L(H) = l，例如，对 H =01**1，H 的串长 L(H)=5.

\quad\quad 定义 1.5 定义距 (Defining Length)

\quad\quad 模式 H 中第一确定字符（从左算起，也可从右算起）和最后一个确定字符的距离，即最后一个确定字符的位数减去第一个确定字符的位数，称为该模式 H 的定义距，记做 $\delta$(H)。例如，H₃ = 01**1， $\delta$(H₃)= 5 - 1 = 4; H₄ =*01**0*1，$\delta$(H₄) = 8 - 2 = 6.

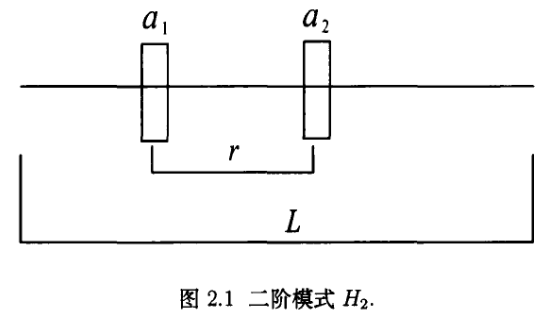
\quad\quad 模式也可用示意图表示，具体方式为，在一条线段上标记出确定位及字符、串长、定义距，如对一个二阶模式 H，在确定位 d₁，d₂ 的确定字符分别为 a₁，a₂，且该模式的串长为 L，定义距为 r，我们只用确定字符来表示该模式，如图 2.1 所示。

\quad\quad 定义 1.6 模式 H 的平均适应度 $f(H,t)$

\quad\quad 设 P ( t ) = { X 1 , X 2 , ⋅ ⋅ ⋅ , X N } P(t) = \{X_1, X_2, ···, X_N\} P(t)={X1​,X2​,⋅⋅⋅,XN​} 表示第 $t$ 代种群， $Eval(X_i)$ 为 $X_i$ 的适应度：
$$f(H,t)=\frac{1}{|H\cap P(t)|}\sum _{x\in H\cap P(t)}Eval(x)$$

其中，$|H\cap P(t)|$ ：表示模式 $H$ 在种群 $P(t)$ 中出现的总数

\quad\quad 下面介绍 Holland 给出的模式定理 (Schema Theorem)，有的研究者把它看作遗传算法的理论基础，它从遗传动力学的角度提供了能够较好的解释遗传算法机理的一种数学工具，同时也是编码策略、遗传策略等分析的基础.模式定理被称为遗传算法遗传动力学的基本定理。该定理反映了重要基因的发现过程。重要基因的结合对应于较高的适应值，说明了它们代表的个体在下一代有较高的生存能力，是提高群体适应性的遗传方向。当然模式定理还不完善.

\quad\quad 定理 1.7 设经典遗传算法的杂交和变异概率分别为 p_c 和 p_m，模式 H 的定义距为 $\delta$(H)，阶为 O(H)，第 t＋1 代种群 P(t+1) 中含有 H 中元素个数的期望值记为 $E(H\cap P(t+1))$，则有：

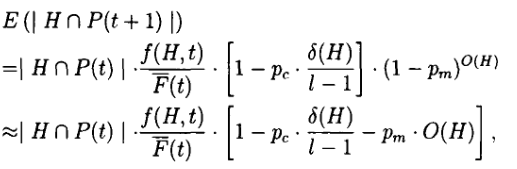
其中，$l$ 为 P(t) 中个体的串长。$\overline{F}(t)={\sum }_{x\in P(t)}Eval(x)/|P(t)|,|H\cap P(t)|$ 为 $P(t)$ 中含于 H 的元素个数。

分别讨论三个遗传算子对模式 H 的生存数量的影响，分三部分:

二、遗传算子对模式生存数量的影响

1、选择算子对模式 H 生存数量的影响

\quad\quad 根据赌轮选择规则，个体被选择的次数与适应度成正比。且每转动一次赌轮，$|H\cap P(t)|$ 中每一个个体被选择次数占种群中个体被选择次数的平均比例(即:平均百分比或被选择的平均概率)为 $f(H,t)/F(t)$，其中：
$$F(t)=\sum _{x\in P(t)}Eval(x)$$

注意到 $H\cap P(t)$ 中含有 $|H\cap P(t)|$ 个体，且每个个体要经受 $N$ 次选择 (转动赌轮 $N$ 次)，故 $H\cap P(t)$ 中元素被选择的次数的期望值 (平均值) 为：
$$|H\cap P(t)|\cdot N\cdot \frac{f(H,t)}{F(t)}=|H\cap P(t)|\cdot \frac{f(H,t)}{\overline{F}(t)}\text{\hspace{1em}(1.3)}$$

其中 $\overline{F}(t)$ 为 $P(t)$ 中个体的平均适应度

\quad\quad 上式 (1.3) 说明下一代群体中模式 H 的生存数量与模式的适应值成正比,与群体平均适应值成反比。当 $f(H,t)>F(t)$ 时, H 的生存数量增加; 当 $f(H,t)<F(t)$ 时，H 的生存数量减少。群体中任一模式的生存数量都将在选择操作中按式 (1.3) 规律变化.

设 $f(H,t)-\overline{F}=c\times \overline{F}$，其中 $c$ 为常数，则式（1.3）改写为：
$$|H\cap P(t)|\cdot \frac{f(H,t)}{\overline{F}(t)}=|H\cap P(t)|\times (\overline{F}+c\times \overline{F})/\overline{F}=|H\cap P(t)|\times (1+c)\text{\hspace{1em}(1.4)}$$

群体从 t = 0 开始操作，假设 $c$ 保持固定不变，则式（1.4）可以表示为：
$$|H\cap P(t)|=|H\cap P(0)|\times (1+c{)}^t$$

\quad\quad 可以看出，在选择算子的作用下，模式的生存数量是以指数函数方式进行变化的。当 $c>0$ 时，模式的生存数量以指数规律增加; 当 $c<0$ 时，生存数量以指数规律减少。这种变化仅仅是已有模式生存数量的变化而已，并没有产生新的模式。

2、杂交算子对模式 H 生存数量的影响

\quad\quad 由于单点杂交是随机选择 $1$ 到 $l-1$ 位置中某一位作为交叉点，然后交换交叉点后的两父母的对应子串，于是只有当交叉点落在 $H$ 的定义距之内的位置，$H$ 才有可能被破坏，但是应注意到，即使交叉点落在定义距位置内，该模式仍有不被破坏的可能。

\quad\quad 故 $H$ 被破坏的概率不超过 $\frac{\delta (H)}{l-1}$ 又因为杂交是以概率 $p_c$ 发生的，故 H 被破坏的概率不超过 $p_c\cdot \frac{\delta (H)}{l-1}$。所以经过杂交后，H 不被破坏 (即生存下来) 的概率至少为 $1-p_c\cdot \frac{\delta (H)}{l-1}$，于是经选择和杂交后，属于模式 H 的元素个数的期望值至少为：
$$|H\cap P(t)|\cdot \frac{f(H,t)}{\overline{F}(t)}\cdot [1-p_c\cdot \frac{\delta (H)}{l-1}]\text{\hspace{1em}(1.5)}$$

\quad\quad 由式 (1.5) 可以看出，交叉操作对模式的影响与其定义距长度 $\delta (H)$ 有关. $\delta (H)$ 越大,模式被破坏的可能性越大。若染色体位串为 $l$, 在单点交叉算子的作用下模式 H 的存活概率 $p_{survival}^c\ge 1-\frac{\delta (H)}{l-1}$。在交叉概率为 $p_c$ 的单点交叉算子的作用下，该模式的存活概率为：
$$p_{survival}^c\ge 1-p_c\cdot \frac{\delta (H)}{l-1}\text{\hspace{1em}(1.6)}$$

那么，模式 H 在选择、交叉算子共同作用下的生存数量可用下式计算：
$$|H\cap P(t)|\ge |H\cap P(t)|\cdot \frac{f(H,t)}{\overline{F}(t)}\times p_{survival}^c\ge |H\cap P(t)|\cdot \frac{f(H,t)}{\overline{F}(t)}\times [1-p_c\cdot \frac{\delta (H)}{l-1}]\text{\hspace{1em}(1.7)}$$

\quad\quad 可见，在选择算子和交叉算子的共同作用下，模式 $H$ 生存数量的变化与其平均适应值及定义距 $\delta (H)$ 密切相关。当 $f(H,t)>F(t)$，且 $\delta (H)$ 较小时，群体中模式生存数量以指数级增长；反之，则以指数级减少。

3、变异算子对模式 H 生存数量的影响

\quad\quad 因为对变异后的每个个体,其每一位发生变异的概率为 $p_m$, 所以该位不发生变异的概率为 $1-p_m$，而模式 H 在变异算子的作用下，若要不受破坏 (即生存下来)，其确定字符在变异时必须不发生变化，而模式的阶为 O(H)，因此在变异算子的作用下 H 不被破坏的概率为 $(1-p_m{)}^{O(H)}$

\quad\quad 综上所述，故经选择、杂交和变异三个遗传算子作用后，$P(t+1)$ 含有 $H$ 中元素个数的期望值应满足：
$$E(|H\cap P(t+1)|)\ge |H\cap P(t)|\cdot \frac{f(H,t)}{\overline{F}(t)}\cdot [1-p_c\cdot \frac{\delta (H)}{l-1}]\cdot (1-p_m{)}^{O(H)}$$

当 $p_m\ll 1，p_c\ll 1$ 时， $(1-p_m{)}^{O(H)}\approx (1-p_m\cdot O(H)$，且
$$(1-p_c\cdot \frac{\delta (H)}{l-1})\cdot (1-p_m\cdot O(H)\approx 1-p_c\cdot \frac{\delta (H)}{l-1}-p_m\cdot O(H)\text{\hspace{1em}(1.8)}$$

再注意到由上不等式 (1.8) 及三个遗传算子对模式的生存数量的影响分析,可以得出以下结论：
$$E(|H\cap P(t+1)|)\ge |H\cap P(t)|\cdot \frac{f(H,t)}{\overline{F}(t)}\cdot [1-p_c\cdot \frac{\delta (H)}{l-1}]\cdot (1-p_m{)}^{O(H)}\approx |H\cap P(t)|\cdot \frac{f(H,t)}{\overline{F}(t)}\cdot [1-p_c\cdot \frac{\delta (H)}{l-1}-p_m\cdot O(H)]$$

结论成立。

\quad\quad 推论 1.8 在经典遗传算法中，低阶、短定义距且适应度高于平均适应度的模式 H，在子代种群中数目的期望值以指数级增加。

\quad\quad 说明： 假设某一特定模式 H 的适应值满足下面条件:

\quad\quad （1）对 $\forall t^{\prime }\le t$
$$\frac{f(H,t^{\prime })}{\overline{F}(t^{\prime })}>c>1$$

\quad\quad （2）$c\cdot [1-p_c\cdot \frac{\delta (H)}{l-1}]>k>1,$ 由上面定理 1.7 和推论 1.8 可以得到以下模式定理

\quad\quad 定理 1.9 (模式定理) 在遗传算子选择、交叉和变异的作用下，那些低阶、短定义距、高适应值的模式的生存数量，将随着迭代次数的增加而以指数级增长。

\quad\quad 将具有低阶、短定义距及高适应度的模式称为积木块 (Building Block)。低阶、短定义距及高于平均适应度的模式在遗传算子的作用下，相互结合，能生成高阶、长定义距，更高平均适应度的模式，并可最终生成全局最优解。这就是重要积木块假设，但它很不严密。由于遗传算法的求解过程并不是在搜索空间中逐一的测试各个基因的枚举组合，而是通过一些较好的模式，像搭积木一样，将它们拼接在一起，从而逐渐的构造出适应度越来越高的个体编码串。

三、块假设、隐含并行性和收敛性

积木块假设

\quad\quad 积木块就是具有低阶 、短定义距以及高适应度的模式．遗传算法在求解过程中通过一些更优的模式，拼接的方式像搭积木一样， 相互结合 ，以此构造出生长阶数高 、适应度高的模式 ，逐渐生成全局最优解．

• 积木块假设： 个体的积木块通过选择、交叉、变异等遗传算子的作用，能够相互结合在一起，形成高阶、长距、高平均适应度的个体编码串（更优质的积木块，从而趋向于全局最优解）。

隐含并行性

\quad\quad 遗传算法在改进过程中，除了被杂交和变异算子破坏的长度长的高阶模式之外 ，遗传算法隐含处理了大量的模式，当处理数量相对较少的串时 ，如在变量个数为 ｎ，ｌ 是 长 度 的 种群，含有 $2^l$ 到 $n\times 2^l$ 个不同的迭代模式，迭代产生的模式数目大于变量的个体数目．Holland 教 授创造的模式定理处理的迭代模式个数为 $O(n^3)$．根据隐含并行性，模式定理说明所有模式都不会被以大生存概率处理，因 此 ，在初始化种群时 ，个体应当具有比较大的差异，通过引入新的模式的变异算子也会增加种群中个体的多样性．

收敛性

\quad\quad 遗传算法的收敛性是关系到算法是否可以实现的关键问题，通常是指其适应值函数的最大或平均值随迭代趋于优化问题的最优值， 或遗传算法所生成的迭代种群（或其分布 ）收敛全局最优解．

使用改进选择算子、交叉算子与变异算子的遗传算法能收敛于最优解的概率为 98％，得 到 的 最小误差小于２％，就认为 找 到 最 优 个 体，这 为 寻 求最优解的循环迭代过程提供了保证．需 要 指 出 的 是 ，每次迭代运行的结果都不相同，要 不 断 查 找 细 节 上 的 不 足 ，力 争 使 结 果 趋 于 稳 定 ．