【智能优化算法】萤火虫优化算法 (Firefly algorithm，FA)，2009

前言

萤火虫优化算法(Firefly algorithm，FA)。由英国剑桥大学的 Yang 等人于 2009 年提出，主要模拟了萤火虫根据个体亮度而相互吸引的行为。作为最新的群智能优化算法之一 , 该算法具有更好的收敛速度和收敛精度 , 且易于工程实现等优点。

截止到 2023 年，算法引用趋势

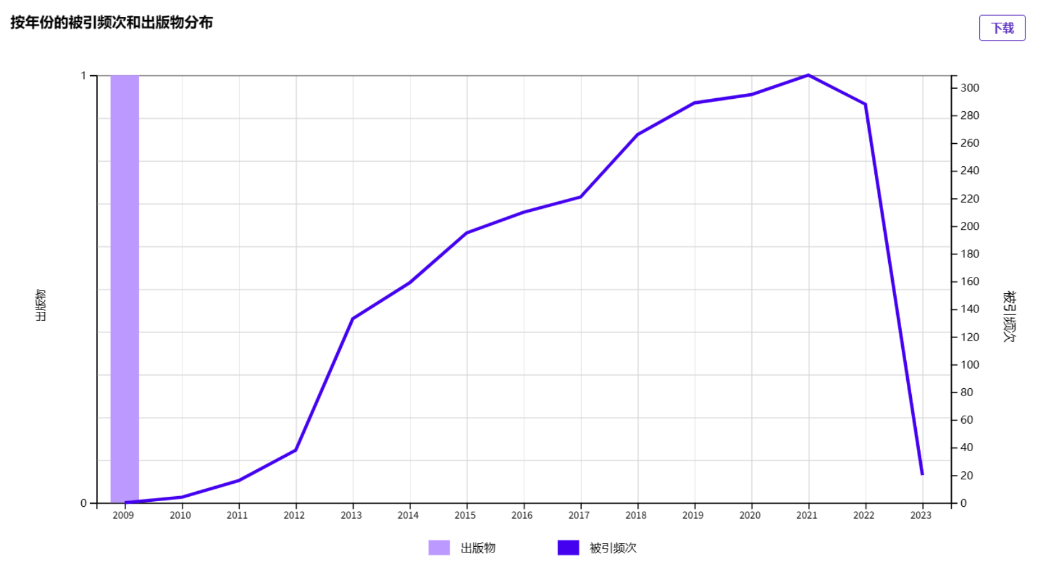
1、FA算法和PSO引用量对比，二十分之一
2、FA算法的引用量逐年上升
3、除了PSO，比较多的是蚁群和蜂群算法

1. 萤火虫相关的生物行为

萤火虫通过下腹的一种化学反应-生物发光（bioluminescence）。这种生物发光是萤火虫求偶仪式的重要组成部分，也是雄性萤火虫和雌性萤火虫交流的主要媒介，发出光也可用来引诱配偶或猎物，同时这种闪光也有助于保护萤火虫的领地，并警告捕食者远离栖息地。

该算法的建立基于两个关键的概念：发出的光的强度和两个萤火虫之间产生的吸引力的程度。

在 FA 中 , 萤火虫发出光亮的主要目的是作为一个信号系统 , 以吸引其他的萤火虫个体 , 其假设为:

1. 萤火虫不分性别 , 它将会被吸引到所有其他比它更亮的萤火虫那去 ;
2. 萤火虫的吸引力和亮度成正比 , 对于任何两只萤火虫 , 其中一只会向着比它更亮的另一只移动 , 然而 , 亮度是随着距离的增加而减少的 ;
3. 如果没有找到一个比给定的萤火虫更亮 , 它会随机移动 。

2. 算法仿生设计

如上所述 , 萤火虫算法包含两个要素 , 即亮度和吸引度. 亮度体现了萤火虫所处位置的优劣并决定其移动方向 , 吸引度决定了萤火虫移动的距离 , 通过亮度和吸引度的不断更新 , 从而实现目标优化. 从数学角度对萤火虫算法的主要参数进行如下描述：

根据物理规律：在距离光源一定距离处的光强服从平方反比定律：
$$I(r)=\frac{I_s}{r^2}\text{\hspace{1em}(2-1)}$$

(1) 萤火虫的相对荧光亮度为：

$$I=I_0{e}^{-\gamma r_{i,j}}\text{\hspace{1em}(2-2)}$$
其中，$I_0$ 为萤火虫的最大荧光亮度，与目标函数值相关，目标函数值越优自身亮度越高； $\gamma$ 为光强吸收系数(通常取值 0.01), 荧光会随着距离的增加和传播媒介的吸收逐渐减弱； $r_{i,j}$ 为萤火虫 $i$ 与 $j$ 之间的空间距离

(2) 萤火虫的吸引度为:

$$\beta ={\beta }_0\ast e^{-\gamma r_{i,j}^2}\text{\hspace{1em}(2-3)}$$
其中，${\beta }_0$ 为最大吸引度；$\gamma$ 为光强吸收系数； $r_{i,j}$ 为萤火虫 $i$ 与 $j$ 之间的空间距离

(3) 萤火虫 $i$ 被吸引向萤火虫 $j$ 移动的位置更新公式如式 (2-4) 所示 :

$$x_i^{t+1}=x_1^t+\beta \ast (x_j^t-x_i^t)+\alpha \ast {ϵ}_i^t\text{\hspace{1em}(2-4)}$$
其中，$x_i^t$, $x_j^t$ 为萤火虫 $i,j$ 所处的空间位置；$\alpha \in$ [0, 1] 为步长因子； ${ϵ}_i^t=(\text{rand}-1/2$)，$\text{rand}$ 为 [0,1] 上服从均匀分布的随机数。

3. 算法流程

• （1） 初始化萤火虫算法参数.

• （2） 计算各萤火虫的亮度并排序得到亮度最大的萤火虫位置.

• （3）判断迭代是否结束：判断是否达到最大迭代次数 T ，达到则转（4），否则转（5）.

• （4） 输出亮度最大的萤火虫位置及其亮度.

• （5） 更新萤火虫位置：根据式（2-4）更新萤火虫的位置，对处在最佳位置的萤火虫进行随机扰动，搜索次数增加 1 ，转（2），进行下一次搜索.

4. 算法特点

1、借鉴了萤火虫根据发光强度相互吸引的特点，但是简化了很多东西，比如雌雄、发光的模式如闪烁频率等

2、算法需要调整的参数有点多

3、原文提出时是针对多模态问题，但是文中未对多模态如何有效等进行说明，仅仅是在实验上说明多模态更有效

4、推测原因如下：和PSO更新公式挺像，但是去掉了gBest，相当于只是向一个比自己好的个体学习，极大降低算法整体收敛速度，增大了开发的时间和范围从仿生的角度来讲，萤火虫相互吸引是从个体的角度出发的，而且发光强弱只代表对萤火虫的吸引力（从个体角度出发），而不是最优食物或者最优捕食地点的信息（从群体角度出发），所以觉得该算法从仿生的角度出发，并没有考虑到一个群智能在里面，更多的像是个体智能

5. 算法相关改进

由于跟随的人不多，改进都比较常规
– Firefly representation (Either Binary of real value)
– Scheme of Population (Swarm or Multi-Swarm)
– Best Solution calculation (Elitism or non-Elitism)
– Movement of Fireflies can be Uniform, Levy Flights, Gaussian, chaos distribution)
参数自适应控制
混合算法

Kumar, V., Kumar, D. A Systematic Review on Firefly Algorithm: Past, Present, and Future. Arch Computat Methods Eng 28, 3269–3291 (2021).

6. 代码实现（chatGPT）

function [bestX, bestF] = firefly_algorithm(fitness_func, lb, ub, dim, max_gen, pop_size, alpha, beta_min, gamma)
% 萤火虫算法
% fitness_func - 适应度函数
% lb - 自变量下界
% ub - 自变量上界
% dim - 自变量维度
% max_gen - 最大迭代次数
% pop_size - 种群大小
% alpha - 衰减常数
% beta_min - 最小吸引度
% gamma - 步长
    % 初始化种群
    pop = create_population(lb, ub, dim, pop_size);
    % 计算适应度
    fitness = evaluate_fitness(fitness_func, pop, pop_size);
    % 寻找最优解
    [bestF, bestIdx] = min(fitness);
    bestX = pop(bestIdx, :);
    % 迭代优化
    for gen = 1:max_gen
        % 更新萤火虫位置
        for i = 1:pop_size
            for j = 1:pop_size
                if fitness(i) > fitness(j)
                    r = norm(pop(i, :) - pop(j, :));
                    beta = beta_min * exp(-alpha * r^2);
                    pop(i, :) = pop(i, :) + beta * (pop(j, :) - pop(i, :)) + gamma * (rand(1, dim) - 0.5);
                    % 边界处理
                    pop(i, :) = max(pop(i, :), lb);
                    pop(i, :) = min(pop(i, :), ub);
                    % 更新适应度
                    fitness(i) = evaluate_fitness(fitness_func, pop(i, :), 1);
                    % 更新最优解
                    if fitness(i) < bestF
                        bestF = fitness(i);
                        bestX = pop(i, :);
                    end
                end
            end
        end
    end
end
% 初始化种群
function pop = create_population(lb, ub, dim, pop_size)
    pop = repmat(lb, pop_size, 1) + rand(pop_size, dim) .* repmat((ub - lb), pop_size, 1);
end
% 计算适应度
function fitness = evaluate_fitness(fitness_func, pop, pop_size)
    fitness = zeros(pop_size, 1);
    for i = 1:pop_size
        fitness(i) = fitness_func(pop(i, :));
    end
end

function [bestX, bestF] = firefly_algorithm(fitness_func, lb, ub, dim, max_gen, pop_size, alpha, beta_min, gamma)
% 萤火虫算法
% fitness_func - 适应度函数
% lb - 自变量下界
% ub - 自变量上界
% dim - 自变量维度
% max_gen - 最大迭代次数
% pop_size - 种群大小
% alpha - 衰减常数
% beta_min - 最小吸引度
% gamma - 步长

这是函数定义部分，可以看到该函数有9个输入参数，分别为适应度函数、自变量下界、自变量上界、自变量维度、最大迭代次数、种群大小、衰减常数、最小吸引度和步长。函数的输出是最优解和最优解的适应度。

    % 初始化种群
    pop = create_population(lb, ub, dim, pop_size);
    % 计算适应度
    fitness = evaluate_fitness(fitness_func, pop, pop_size);
    % 寻找最优解
    [bestF, bestIdx] = min(fitness);
    bestX = pop(bestIdx, :);

这部分代码是初始化种群，并计算种群中每个个体的适应度。通过调用 create_population 函数初始化种群，然后使用 evaluate_fitness 函数计算种群中每个个体的适应度。接着，寻找种群中的最优解。

    % 迭代优化
    for gen = 1:max_gen
        % 更新萤火虫位置
        for i = 1:pop_size
            for j = 1:pop_size
                if fitness(i) > fitness(j)
                    r = norm(pop(i, :) - pop(j, :));
                    beta = beta_min * exp(-alpha * r^2);
                    pop(i, :) = pop(i, :) + beta * (pop(j, :) - pop(i, :)) + gamma * (rand(1, dim) - 0.5);
                    % 边界处理
                    pop(i, :) = max(pop(i, :), lb);
                    pop(i, :) = min(pop(i, :), ub);
                    % 更新适应度
                    fitness(i) = evaluate_fitness(fitness_func, pop(i, :), 1);
                    % 更新最优解
                    if fitness(i) < bestF
                        bestF = fitness(i);
                        bestX = pop(i, :);
                    end
                end
            end
        end
    end

这部分代码是迭代优化过程。对于每个萤火虫，它会被其他萤火虫的发光吸引，且吸引度与两个萤火虫之间的距离成反比。然后，萤火虫会向较亮的那个萤火虫靠近，并在吸引度和步长的影响下更新位置。更新后的位置需要进行边界处理，并重新计算适应度，更新最优解。

end
% 初始化种群
function pop = create_population(lb, ub, dim, pop_size)
    pop = repmat(lb, pop_size, 1) + rand(pop_size, dim) .* repmat((ub - lb), pop_size, 1);
end
% 计算适应度
function fitness = evaluate_fitness(fitness_func, pop, pop_size)
    fitness = zeros(pop_size, 1);
    for i = 1:pop_size
        fitness(i) = fitness_func(pop(i, :));
    end
end

这部分代码是两个辅助函数，分别用于初始化种群和计算种群中每个个体的适应度。create_population 函数通过随机生成种群中每个个体的自变量值来初始化种群。evaluate_fitness 函数通过调用适应度函数来计算种群中每个个体的适应度。
总的来说，这段代码实现了萤火虫算法，并可以用于求解连续优化问题。它通过模拟萤火虫在夜空中的闪烁行为，来寻找最优解。

References

[1] Yang X S, Deb S. Eagle strategy using l´ evy walk and firefly algorithms for stochastic optimization. Nature Inspired Cooperative Strategies for Optimization (NICSO 2010), Berlin Heidelberg: Springer, 2010. 101−111

[2] 智能优化算法：萤火虫算法-附代码