一、算法来源
1、DBSCAN算法原型
这个算法原型非常简单,有很多博主都有写,大家自己去看看就好了,也不用花太多时间,顶多十分钟就能了解个大概。
2、自适应Eps和Minpts参数
由于该算法对Eps和Minpts参数十分敏感,所以如何确定这两个参数对于DBSCAN来说是很重要的一步,这篇博文是基于李文杰老师的论文《自适应确定DBSCAN算法参数的算法研究》,通过这篇论文,输入数据集即可大致确定这两个参数,从而可以直接在DBSCAN中应用。
二、大致思想
其中的基本思想,是通过计算数据集 D 中每个数据点与其第 K个最近邻数据点之间的 K-最近邻距离,并对所有数据点的 K-最近邻距离求平均值,这个值就作为这个k时的eps,那么每一个k对应一个K-最近邻距离平均值(K=1时,即为平均最近邻距离),所以每一个k都对应一个eps。这时我们可以想一下它的物理意义,这个eps其实就是K-近邻距离最大的那个半径的平均。
然后论文又根据下面这个公式计算出Minpts。
式中,Pi 为第 i 个对象的 Eps 邻域对象数量,n 为数据集 D 中的对象总数
随后用这些结果尝试使用DBSCAN算法进行聚类,如果连续的候选项聚类的类别数目相同,那么选择Eps相对较大的那个最为最终参数输入到DBSCAN算法中去。
论文中认为如果连续3个Eps候选项聚类的类别数目相同,那么可以认为数据集在这些参数下逐渐收敛,但是我觉得具体最好看图像是否收敛,所以我就简单的在程序里将聚类数目打印出来,读者可以自行选择聚利时使用的Eps和Minpts参数。
具体python程序:
import math
import copy
import numpy as np
from sklearn.cluster import DBSCAN
import pandas as pd
import matplotlib.pyplot as plt
#两个样本点之间的欧式距离
def dist(a,b):
"""
:param a: 样本点
:param b: 样本点
:return: 两个样本点之间的欧式距离
"""
return math.sqrt(math.pow(a[0]-b[0],2) + math.pow(a[1]-b[1],2))
#第k最近距离集合
def returnDk(matrix,k):
"""
:param matrix: 距离矩阵
:param k: 第k最近
:return: 第k最近距离集合
"""
Dk = []
for i in range(len(matrix)):
Dk.append(matrix[i][k])
return Dk
#第k最近距的平均即eps
def returnDkAverage(Dk):
"""
:param Dk: k-最近距离集合
:return: Dk的平均值
"""
sum = 0
for i in range(len(Dk)):
sum = sum + Dk[i]
return sum/len(Dk)
#传入数据计算距离矩阵
def CalculateDistMatrix(dataset):
"""
:param dataset: 数据集
:return: 距离矩阵
"""
DistMatrix = [[0 for j in range(n)] for i in range(n)]
for i in range(n):
for j in range(n):
DistMatrix[i][j] = dist(dataset[i], dataset[j])
return DistMatrix
#传入数据和k输出eps,min_samples以及聚类簇的个数
#n=len(X),DistMatrix = CalculateDistMatrix(X)
#n是数据长度,DistMatrix距离矩阵
def ems(dataset,k):
#深度拷贝距离矩阵依此计算出eps
tmp_matrix = copy.deepcopy(DistMatrix)
for i in range(n):
tmp_matrix[i].sort()
Dk = returnDk(tmp_matrix,k)
eps = returnDkAverage(Dk)
tmp_count = 0
for i in range(len(DistMatrix)):
for j in range(len(DistMatrix[i])):
if DistMatrix[i][j] <= eps:
tmp_count = tmp_count + 1
min_samples=tmp_count/n#参考前述公式
clustering = DBSCAN(eps= eps,min_samples= min_samples).fit(dataset)
num_clustering = max(clustering.labels_)+1
return eps,min_samples,num_clustering
这里程序主要参考CSDN另一篇博文《【聚类】一种自适应Eps和Minpts的DBSCAN方法(python实现)》而实现,在最后一个函数做了一下融合,方便对簇的个数进行判断。我们知道,对于数据进行聚类,如果只是有一个类,那么这个聚类行为将毫无意义,当然对于读者要解决的具体问题而言,对于簇的个数可能有一个更为准确的范围。显然,对于这个程序,当半径eps越来越大时,簇的个数就会变为0,就没有必要继续往下进行计算,这样就大大的减少了计算的复杂度。
执行程序如下
df = pd.read_csv('./datas/检查不合格记录-样本-test(整理).csv')
df1=df[["jcdxjd","jcdxwd","jcsxmc"]]
X=df1[["jcdxjd","jcdxwd"]].values
n=len(X)
DistMatrix = CalculateDistMatrix(X)
E=[]
M=[]
S=[]
for k in range(1,n):
e,m,s = ems(X,k)
if s<3:
break
else:
E.append(e)
M.append(m)
S.append(s)
print(E,M,S)
其中X是从pandas导入的数据集,E,M,S分别是eps,min_samples,簇的个数;s<3条件就是对簇的个数进行限制,当簇的个数小于3个的时候就没有必要再往下进行聚类了,计算速度比原来提升了很多倍。
运行结果:
最后一个列表是簇的个数

eps与k的曲线:

簇的个数与k的曲线:

结合之前说的簇的个数s可以取:16、12、9、5、4、3,对应的k往大的取应该是:17、24、31等等。
论文之外的思考:
其实将论文的整个逻辑连贯起来,它就是将k近邻的半径来将聚类的两个参数联系起来,所以关键还是k和eps的关系。我们联系之前说的物理意义,想象当k不停增大时eps却没有明显的增大,说明eps差不多到了一个簇的最大半径,可以加入更多的数据而不影响eps,所以当k取到这个条件下的最大时,就是一个临界值,是一个聚类参数的合适值之一。这里放原论文的两张图。
Eps参数列表与 K 值的关系曲线:
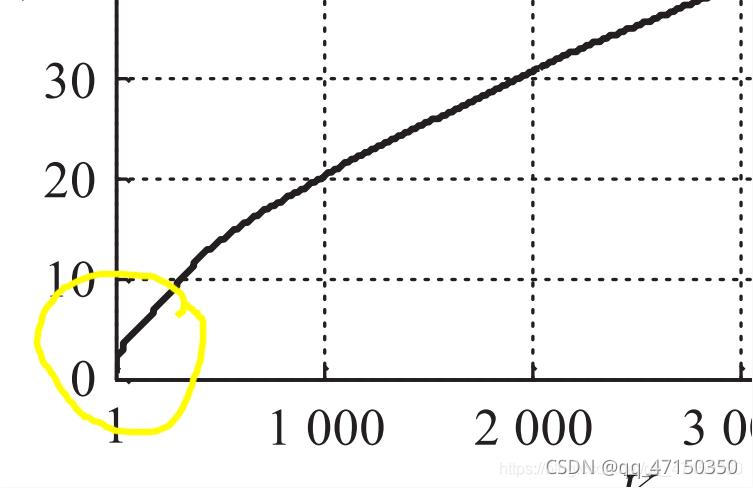
簇的个数与 K 值的关系曲线:

可以看到当k=6时,簇的个数趋于稳定,所以k取6,但我们仔细观察Eps与 K 值的关系曲线可以发现,在大概k=6的位置eps趋于平缓,而后突然增大,与前面所说的eps与k的物理意义一样,eps趋于平缓说明,随着k的增大,eps半径已无明显变化,当eps突然增大的时候,说明到了临界位置,就是我们需要重点考虑的点。
所以我们是可以直接根据Eps与 K 值的关系曲线来确定k值,即确定聚类参数的,这样就可以大大的减少算法的计算量。
我们很容易就想到可以用曲线导数描述前面所说的变化,如下图:

这时我们可以设置一个阈值,只需要选取将接近0然后突然增大的点,然后我们需要的k值就在这些点中,就可以进一步缩小范围,减少计算量。
参考链接:https://blog.csdn.net/liyihao17/article/details/89372581











 本文介绍了一种基于李文杰老师论文的方法,用于自适应地确定DBSCAN算法中的Eps和MinPts参数。该方法通过计算数据集中每个点的K-最近邻距离及其平均值来确定合适的Eps值,并据此计算MinPts。此外,还提供了一个Python程序示例,展示了如何根据数据集调整这些参数并执行聚类。
本文介绍了一种基于李文杰老师论文的方法,用于自适应地确定DBSCAN算法中的Eps和MinPts参数。该方法通过计算数据集中每个点的K-最近邻距离及其平均值来确定合适的Eps值,并据此计算MinPts。此外,还提供了一个Python程序示例,展示了如何根据数据集调整这些参数并执行聚类。
















 388
388

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








