并行加法器（串行进位或者并行进位）

加法器

总述

利用门电路实现一位的加法

二进制的加法，就是很多个加法组成起来的。

1 bit全加器

n bit加法器

不足之处，进位信息是串行的，计算速度取决于进位产生和传递的速度。位数越多，运算速度越慢。

注1：电信号到达稳定态需要一定时间，因此进位产生速度会有延迟。

注2：串行进位又称为行波进位，每一级进位直接依赖于前一级的进位，即进位信号是逐级形成的。

输入是并行的，但是进位方式是串行的。

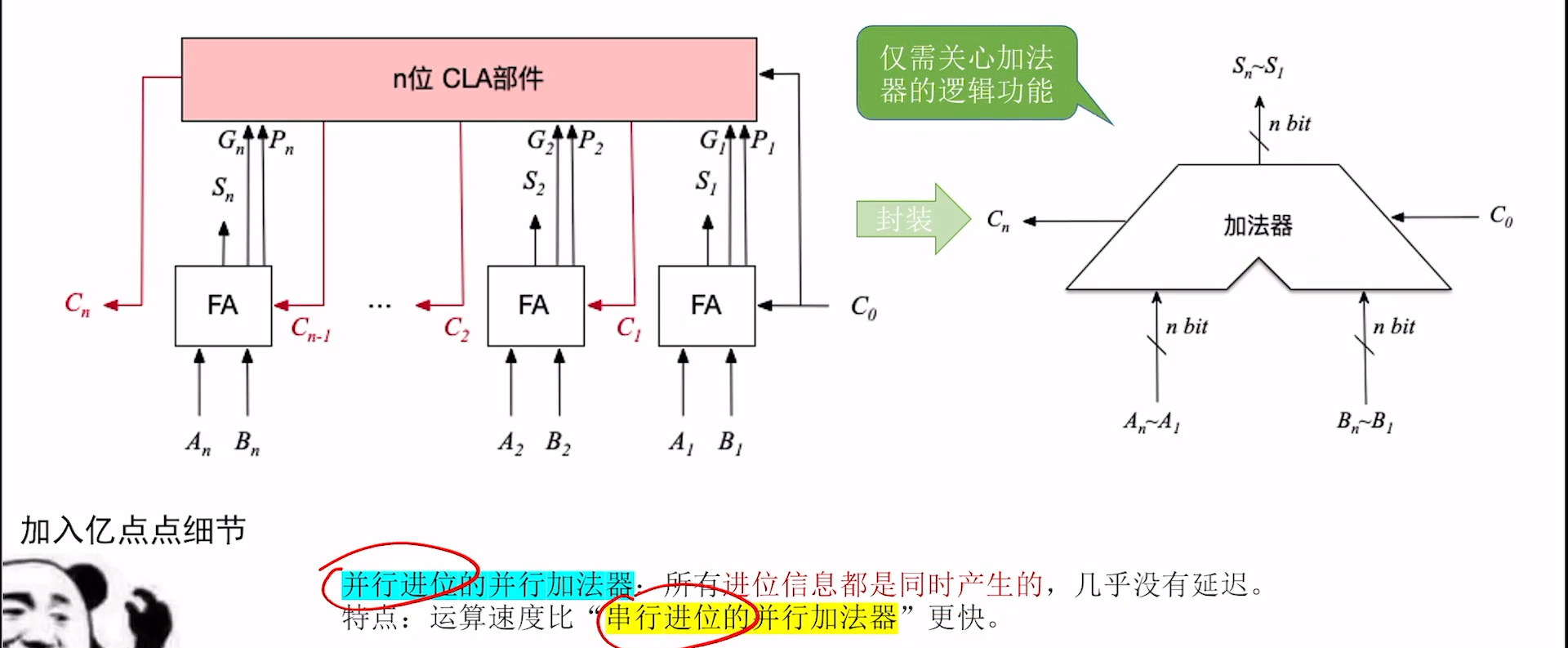
并行进位的并行加法器

增加一个CLA部件。

带标志位的加法器

加法器的范围是有限的，输入数据后，如果超出了范围，那么结果一定是错误的。是否为0的判定，A-B或者A+(-B)。判断A>B？通过判断A+(-B)是否大于0。

关心的问题：①是否溢出?②为0？③正还是负？

标志位为OF、SF、ZF、CF。

带符号数和无符号数表示的范围是不一样的，所以判断溢出的方式也会不一样，所以用两种标志为来表示。带符号数的标志位为OF，无符号数的标志位为CF。

标志位的生成

OF和CF的具体原理，后面补充。

总结

串行进位的并行加法器

如何更快的产生进位

并行加法器的优化

4个全加器，运算逻辑根据这些表达式来设计。由于套娃，线路越来越复杂，所以一般到C4。