【复旦邱锡鹏教授《神经网络与深度学习公开课》笔记】从概率角度看线性回归

从概率角度来看线性回归

从机器学习的角度看，线性回归需要通过一个函数建模$x,y$之间的关系；而从概率的角度看，则是要表示出在给定$x$下随机变量$y$的条件概率。
但通常$y$是一个定值，为了计算$y$在给定$x$下的条件概率$p(y|x)$，首先要将$y$看作一个随机变量。可以先用一个函数表示出一个连续函数，在对该函数进行采样时添加一个服从均值为0方差为${\sigma }^2$的噪声$ϵ$，最后得到连续随机变量$y$的概率密度函数：
$$y=f(x,w)+ϵ,ϵ\in (0,{\sigma }^2)$$

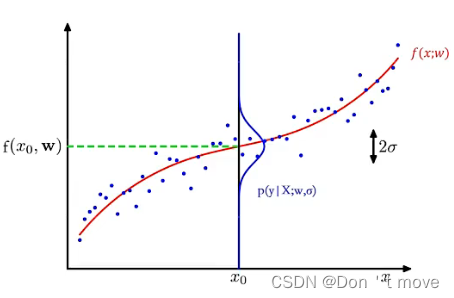
对线性回归来说，$f(x,w)=w^{T}x$，于是$y=w^{T}x+ϵ$，移项得$ϵ=y-w^{T}x$，由于$ϵ$服从高斯分布，它的概率分布函数为：
$$p(ϵ;0,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{(ϵ-0{)}^2}{2{\sigma }^2})=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{(ϵ{)}^2}{2{\sigma }^2})$$
将$ϵ=y-w^{T}x$带入上式¹可得给定$x$下$y$的条件概率：
$$p(y|x;w,\sigma )=\mathcal{N}(y;w^{T}x,{\sigma }^2)=\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{(y-w^{T}x{)}^2}{2{\sigma }^2})$$
这样也可以说$y$是满足均值为$w^{T}x$，方差为${\sigma }^2$的高斯分布，即$y\in \mathcal{N}(w^{T}x,{\sigma }^2)$。由此得出待优化模型。

似然函数（Likehood）

对于$p(x;w)$来说，概率是指在参数$w$固定的情况下，随机变量$x$的概率分布，即将随机变量$x$看作自变量。而与概率相反，似然指已知随机变量$x$的情况下，不同参数$w$的取值对随机变量$x$取值分布的影响，即将参数$w$看作自变量。
对于线性回归，参数$w$在训练集$D$上的似然函数为：
$$p(y|X;w,\sigma )=\prod _{n=1}^{N}p(y^{(n)}|x^{(n)};w,\sigma )=\prod _{n=1}^N\mathcal{N}(y^{(n)};w^T{x}^{(n)},{\sigma }^2)$$
要特别注意其中的自变量是$w$。此外，$y=\left[\begin{array}{c}{y}^{(1)}\\ ⋮\\ y^{(n)}\end{array}\right]$，$X=\left[\begin{array}{cccc}{x}^{(1)}& x^{(2)}& \cdots & x^{(n)}\end{array}\right]$ ，由于$y$和$X$独立同分布²（这里是默认$X$也服从高斯分布），因此整体的似然函数可以分解为每个样本似然函数的连乘。

最大似然估计（Maximum Likelihood Estimate，MLE）

有了似然函数之后，需要通过一个准则来优化似然函数中的参数$w$，使得似然函数最大，这个过程就是最大似然估计，即找到一组参数$w$使得似然函数$p(y|X;w,\sigma )$最大。
同时，对于指数型的似然函数（$e$的n次方，即$\exp$），通常还会在计算偏导数时加上$\log$（这里的$\log$只是表明是对数函数，不单独指以某个值为底数）转换成对数型的似然函数，转换成对数函数之后，在求偏导数时就能将连乘（$\prod$）转换为连加（$\sum$），方便下一步计算。同时，由于$\exp (x)$和${\ln }^x$都单调递增，所以二者的复合仍单调递增（同增异减），函数单调性不变，因此极值点不变。
$$\begin{array}{rl}\frac{\partial \log p(y|X;w,\sigma )}{\partial w}& =\frac{\partial }{\partial w}\log (p(y^{(1)}|x^{(1)};w,\sigma )\cdot p(y^{(1)}|x^{(2)};w,\sigma )\cdots p(y^{(N)}|x^{(N)};w,\sigma ))\\ & =\frac{\partial }{\partial w}(\log p(y^{(1)}|x^{(1)};w,\sigma )+\log p(y^{(1)}|x^{(2)};w,\sigma )+\cdots +\log p(y^{(N)}|x^{(N)};w,\sigma )))\\ & （假设以e为底求导，其他可以参考导数表）\\ & =\frac{1}{p(y^{(1)}|x^{(1)};w,\sigma )}\frac{\partial p(y^{(1)}|x^{(1)};w,\sigma )}{\partial w}+\cdots +\frac{1}{p(y^{(N)}|x^{(N)};w,\sigma )}\frac{\partial p(y^{(N)}|x^{(N)};w,\sigma )}{\partial w}\\ & =\sum _{n=1}^N\frac{1}{p(y^{(n)}|x^{(n)};w,\sigma )}\frac{\partial p(y^{(n)}|x^{(n)};w,\sigma )}{\partial w}\\ & =\sqrt{2\pi }\sigma \frac{1}{\sqrt{2\pi }\sigma }\sum _{n=1}^N\frac{1}{\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})}\frac{\partial }{\partial w}\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})\\ & =-\sum _{n=1}^N\frac{1}{\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})}\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})\frac{\partial }{\partial w}(\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})\\ & =-\sum _{n=1}^N\frac{1}{\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})}\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})(\frac{-2(x^{(n)}{)}^T(y^{(n)}-w^T{x}^{(n)})}{2{\sigma }^2})\\ & =\sum _{n=1}^N\frac{1}{\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})}\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})(\frac{(x^{(n)}{)}^T(y^{(n)}-w^T{x}^{(n)})}{{\sigma }^2})\\ & =\frac{1}{\sigma }\sum _{n=1}^N\frac{1}{\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})}\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})(x^{(n)}{)}^T(y^{(n)}-w^T{x}^{(n)})\\ & =\frac{1}{{\sigma }^2}\sum _{n=1}^N(x^{(n)}{)}^T(y^{(n)}-w^T{x}^{(n)})\\ & =\frac{1}{{\sigma }^2}X(y-X^{T}w)\end{array}$$
算到这里可以看出，啊其实不用这么麻烦，直接用$p(y|X;w,\sigma )$算就行，不用拆开，但是我已经算出来了，那就这样吧。令上式为0
$$\begin{array}{rl}\frac{1}{p(y|X;w,\sigma )}& =0\\ \frac{1}{{\sigma }^2}X(y-X^{T}w)& =0\\ Xy-X{X}^{T}w& =0\\ X{X}^{T}w& =Xy\\ w& =(X{X}^T{)}^{-1}Xy\\ w& =(X^T{)}^{-1}y\end{array}$$
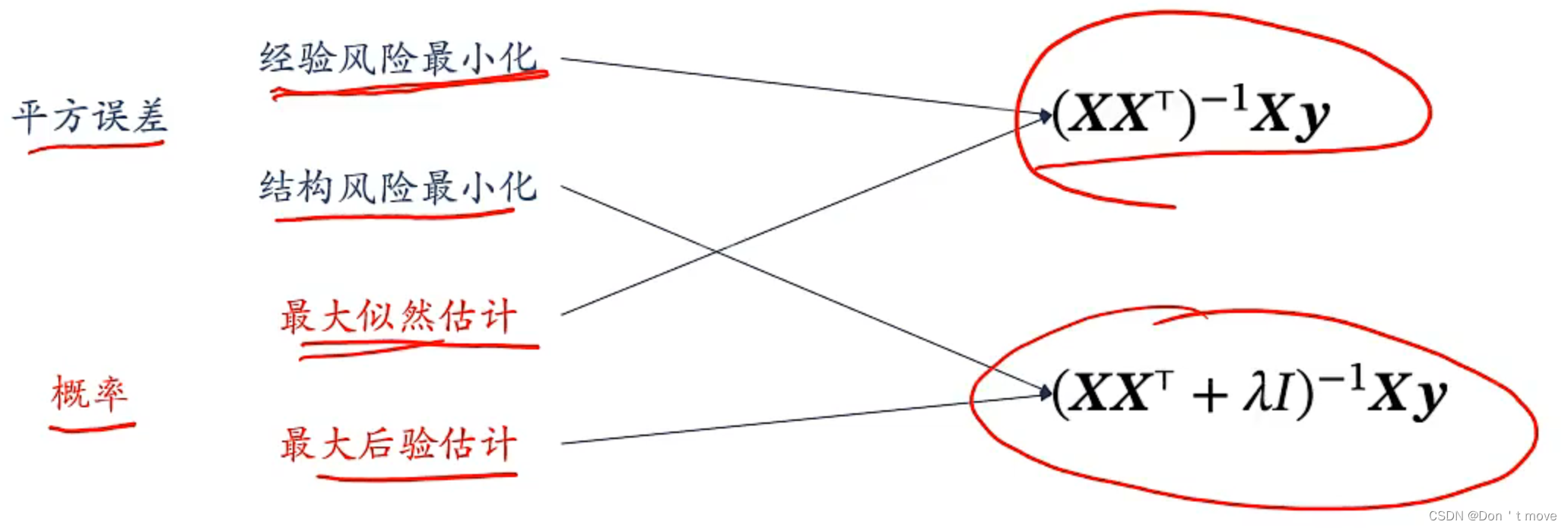
由此可见最大似然估计的解与经验风险最小化ERM的解相同

从贝叶斯的角度来看线性回归

从贝叶斯的视角来看，需要将可能影响结果的因素作为随机变量添加到计算当中，对于回归问题来说，就是需要将参数$w$也看作随机变量而不是一个给定的参数，将对$w$的估计变成对$w$分布的估计，目标是求在给定观测数据$(x,y)$的条件下$w$的条件概率$p(w|x,y)$。这种已知观测数据，由观测数据得到的分布叫做后验分布³；然后，还有先验分布，就是在没有观测数据支持的情况下，直接根据经验给出分布，即$p(w)$；最后还有之前提到的似然估计，就是在已知$w$的情况下来估计观测数据$(x,y)$的概率$p(x,y|w)$。后验、先验、似然是贝叶斯问题中三个相似的概念，三者都要将回归问题中的$w$作为随机变量。
在回归问题中，为了求解$w$，先验分布、后验分布、似然估计分别表示为

先验分布	后验分布	似然估计
$p(w)$	$p(w\mid X,y)$	$p(y\mid X,w)$

接下来，假设三个随机变量都服从以$v$为均值、$\sigma$为方差的分布，根据条件概率公式可得
$$p(w\mid X,y;v,\sigma )=\frac{p(w,X,y;v,\sigma )}{p(X,y;v,\sigma )}$$
由概率的乘积的定义可知，$w,X,y$同时发生的概率也就是$p(w,X,y)=p(w)p(X,y\mid w)=p(w)p(X\mid w)p(y\mid X,w)$，然后由于在机器学习问题中$X$的取值与$w$无关，所以$p(X\mid w)=p(X)$，因此
$$\begin{array}{rl}p(w\mid X,y;v,\sigma )& =\frac{p(w;v,\sigma )p(X;v,\sigma )p(y\mid X,w;v,\sigma )}{p(X,y;v,\sigma )}\\ & =\frac{p(w;v,\sigma )p(X;v,\sigma )p(y\mid X,w;v,\sigma )}{p(X;v,\sigma )p(y\mid X;v,\sigma )}\\ & =\frac{p(w;v,\sigma )p(y\mid X,w;v,\sigma )}{p(y\mid X;v,\sigma )}\end{array}$$
也可以套贝叶斯公式⁴得到
$$\begin{array}{rl}p(w\mid X,y)& =\frac{p(w)p(X,y\mid w)}{{\sum }_{w}p(w)p(X,y\mid w)}\\ & =\frac{p(w)p(X\mid w)p(y\mid X,w)}{{\sum }_{w}p(w)p(X\mid w)p(y\mid X,w)}\\ & =\frac{p(w)p(X)p(y\mid X,w)}{{\sum }_{w}p(w)p(X)p(y\mid X,w)}\\ & =\frac{p(w)p(y\mid X,w)}{{\sum }_{w}p(w\mid X)p(y\mid X,w)}\\ & =\frac{p(w)p(y\mid X,w)}{{\sum }_{w}p(w,y\mid X)}\end{array}$$
在实际应用中，通常只关注与之前提到过的后验、先验和似然，从上式可以看出后验分布和先验分布与似然估计的乘积成正比，记作$p(w\mid X,y)\propto p(w)p(y\mid X,w)$。
同样的为了方便计算，将后验分布转换为对数形式计算
$$\begin{array}{rl}\log p(w\mid X,y;v,\sigma )& \propto \log (p(w;v,\sigma )p(y\mid X,w;v,\sigma ))\\ & \propto \log p(w;v,\sigma )+\log p(y\mid X,w;v,\sigma )\end{array}$$
假设（先验，所以假设）$w$取值服从以0为均值、方差为$v^{2}I$（$I$为单位矩阵）的高斯分布，则
$$\begin{array}{rl}p(w;v,\sigma )& =\mathcal{N}(w;0,v^{2}I)\\ & =\frac{1}{\sqrt{2\pi }v}\sum _{n=1}^D\exp (-\frac{(w^{(n)}{)}^2}{2v^2})\\ \log p(w;v,\sigma )& =\sum _{n=1}^D(\log \exp (-\frac{(w^{(n)}{)}^2}{2v^2})-\frac{1}{2}\log 2\pi v^2)\\ & =\sum _{n=1}^D(-\frac{(w^{(n)}{)}^2}{2v^2}-\frac{1}{2}\log 2\pi v^2)\\ & =-\frac{1}{2v^2}{w}^{T}w-\frac{D}{2}\log 2\pi v^2\end{array}$$
同时，前面在从概率视角看的时候提到过，$y$是服从$\mathcal{N}(y;w^{T}x,{\sigma }^2)$的高斯分布（似然），则
$$\begin{array}{rl}p(y\mid X,w;v,\sigma )& =\prod _{n=1}^N\mathcal{N}(y^{(n)};w^T{x}^{(n)},{\sigma }^2)\\ \log p(y\mid X,w;v,\sigma )& =\sum _{n=1}^N\log (\frac{1}{\sqrt{2\pi }\sigma }\exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2}))\\ & =\sum _{n=1}^N(\log \exp (-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2})-\frac{1}{2}\log 2\pi {\sigma }^2)\\ & =\sum _{n=1}^N(-\frac{(y^{(n)}-w^T{x}^{(n)}{)}^2}{2{\sigma }^2}-\frac{1}{2}\log 2\pi {\sigma }^2)\\ & =-\frac{1}{2{\sigma }^2}\parallel y-X^{T}w{\parallel }^2-\frac{N}{2}\log 2\pi {\sigma }^2\end{array}$$
代入上面关系式
$$\begin{array}{rl}& \log p(w;v,\sigma )+\log p(y\mid X,w;v,\sigma )\\ & =-\frac{1}{2v^2}{w}^{T}w-\frac{D}{2}\log 2\pi v^2-\frac{1}{2{\sigma }^2}\parallel y-X^{T}w{\parallel }^2-\frac{N}{2}\log 2\pi {\sigma }^2\\ & =-\frac{1}{2{\sigma }^2}\parallel y-X^{T}w{\parallel }^2-\frac{1}{2v^2}{w}^{T}w-C\\ & \propto -\frac{1}{2{\sigma }^2}\parallel y-X^{T}w{\parallel }^2-\frac{1}{2v^2}{w}^{T}w\\ & 令\lambda =\frac{{\sigma }^2}{v^2}，则v^2=\frac{{\sigma }^2}{\lambda }\\ 原式& \propto -\frac{1}{2{\sigma }^2}\parallel y-X^{T}w{\parallel }^2-\frac{\lambda }{2{\sigma }^2}{w}^{T}w\\ & =-\frac{1}{{\sigma }^2}(\frac{1}{2}\parallel y-X^{T}w{\parallel }^2+\frac{\lambda }{2}{w}^{T}w)\\ & \propto \frac{1}{2}\parallel y-X^{T}w{\parallel }^2+\frac{\lambda }{2}{w}^{T}w\end{array}$$
这里需要解释一下为什么在乘了负号之后仍然成正比：因为本身最优化问题就是求解函数的极值，从极大值变成极小值对于函数来说没有什么影响，所以虽然严格意义上乘以负号之后确实与原函数成反比，但对于最优化问题来说二者是成正比的，其实也可以说对于概率的最优化问题来说，函数乘以任意常数后仍然成正比。
算到这里可以看出实际上贝叶斯回归的待优化函数与带正则化项的结构风险函数是一样的，因此可以说结构风险函数与后验分布成正比，记作$\hat{R}(w)\propto -\log p(w)$（带不带负号不影响）
有了后验分布，可以通过后验分布得到模型的期望
$$\begin{array}{rl}y& ={\mathbb{E}}_{w\sim p(w\mid X,y)}[f(X,y,w)]\\ & ={\int }_{\mathbb{R}}f(X,y,w)p(w\mid X,y)dw\end{array}$$
这种方法直接通过$w$的后验分布计算得到模型的期望，整个过程中虽然$w$的值都是固定不变的，但每次都需要通过积分去计算期望，无疑加大了计算量。因此，更为可行的方法还是需要计算出参数$w$的期望，在贝叶斯估计中可以用点估计的方法来完成这个操作。
所谓点估计，就是估计出一个实际的点而不是分布，对于机器学习来说，也就是需要通过后验分布来估计出一个最优的参数$w$取值，从而避免直接使用后验分布进行计算，这个过程叫做最大后验估计（Maximum A Posterior Estimation，MAP）
$$w^{MAP}={\mathrm{argmax}}_{w}p(y\mid X,w;\sigma )p(w;v)$$
$$\begin{array}{rl}& \frac{\partial }{\partial w}\log (p(y\mid X,w;\sigma )p(w;v))\\ & =\frac{\partial }{\partial w}(\log p(y\mid X,w;\sigma )+\log p(w;v))\\ & =\frac{\partial }{\partial w}(-\frac{1}{2{\sigma }^2}\parallel y-X^{T}w{\parallel }^2-\frac{N}{2}\log 2\pi {\sigma }^2-\frac{1}{2v^2}{w}^{T}w-\frac{D}{2}\log 2\pi v^2)\\ & =\frac{\partial }{\partial w}(-\frac{1}{2{\sigma }^2}(y-X^{T}w{)}^T(y-X^{T}w)-\frac{N}{2}\log 2\pi {\sigma }^2-\frac{1}{2v^2}{w}^{T}w-\frac{D}{2}\log 2\pi v^2)\\ & =-\frac{1}{{\sigma }^2}X(y-X^{T}w)-\frac{1}{v^2}w\end{array}$$
$$\begin{array}{rl}-\frac{1}{{\sigma }^2}X(y-X^{T}w)-\frac{1}{v^2}w& =0\\ -\frac{1}{{\sigma }^2}Xy+\frac{1}{{\sigma }^2}X{X}^{T}w-\frac{1}{v^2}w& =0\\ (\frac{1}{{\sigma }^2}X{X}^T-\frac{1}{v^2})w& =\frac{1}{{\sigma }^2}Xy\\ (X{X}^T-\frac{{\sigma }^2}{v^2})w& =Xy\\ w& =(X{X}^T-\frac{{\sigma }^2}{v^2}{)}^{-1}Xy\end{array}$$
即$w^{MAP}=(X{X}^T-\frac{{\sigma }^2}{v^2}{)}^{-1}Xy$（视频里错了，这里有个算的一样的⁵），也就是说最大后验估计的结果与结构风险最小化SRM结果一致。

---

1. 最大似然估计：从概率角度理解线性回归的优化目标 - 知乎 (zhihu.com) ↩︎

2. 独立同分布 independent and identically distributed - 知乎 (zhihu.com) ↩︎

3. 一个例子搞清楚（先验分布/后验分布/似然估计）-CSDN博客 ↩︎

4. 条件概率、全概率公式、贝叶斯公式 - 知乎 (zhihu.com) ↩︎

5. 线性模型参数求解的最大似然估计、MAP估计、正则最小二乘估计_双月实验map估计-CSDN博客 ↩︎