压缩感知、一阶范数、Lasso

压缩感知

什么是可压缩信号：
$$\mathbf{x}=\mathbf{\Psi }\mathbf{s}$$
信号$\mathbf{x}$代表原始信号信号（时域空间），$\Psi$是转换基，$\mathbf{s}$是$k-\text{稀疏}$信号,代表有$K$ 个非零值。

这个式子表明，只要是能够在另一个空间表示的信号基本都可以被压缩，比如在时域中的信号在傅里叶空间中可以表示，所以时域信号就可以压缩。

假设有信号
$$\begin{gathered} \mathbf{y}=\mathbf{x}(\mathbf{t})+\text{Noise} \\ \mathbf{x}(\mathbf{t})=\mathbf{s}\mathbf{i}\mathbf{n}(\mathbf{a}\mathbf{t})+\mathbf{c}\mathbf{o}\mathbf{s}(\mathbf{b}\mathbf{t}) \end{gathered}$$
假设噪音信号的振幅远低于$\mathbf{x}(\mathbf{t})$ ,那么经过傅里叶转换后在频域中$\mathbf{y}$就是几条垂直的直线

clc,clear
t = [0:0.01:10];
y = sin(2*pi*t)+cos(30*pi*t) + randn(1,length(t));
z = fft(y);
f = [0:0.001:1];
stem(abs(z))

上图画的是点图，其余密集的坐标上其实都是有值的，但是它们对信息的保留基本毫无意义，所以只要在频域里保留这几条直线信息，就可以实现数据的压缩。

一般压缩方法：将所有数据都使用傅里叶或者其他转换方法转换到另一个空间然后对数据进行过滤，舍弃掉大多数不重要的信息。

压缩感知：随机抽取一些采样数据，然后推测转换空间里的稀疏性，我的理解是因为傅里叶转换等方法依旧会保留信息的距离关系，所以只需要一些随机采样就可以推测所有数据在转换空间的稀疏程度。

instead of collecting high-dimensional data just to compress and discard most of the information, it is instead possible to collect surprisingly few compressed or random measurements and then infer what the sparse representation is in the transformed basis

所以只需要从$\mathbf{x}$中得到不多的采样就有可能可以将信号压缩，而不是将所有的信号都测量一边再压缩（筛除），即：
$$\mathbf{y}=\mathbf{C}\mathbf{x}$$
矩阵$\mathbf{C}$就是采样矩阵，采样矩阵可以是一个随机矩阵，可以是高斯或者伯努利分布的随机矩阵（矩阵中每一个值都是服从分布的），采样矩阵从原始信号中抽取少量样本。

所以在频域中稀疏的采样值可以表示为：
$$\mathbf{y}=\mathbf{C}\mathbf{\Psi }\mathbf{s}=\mathbf{\Theta }\mathbf{s}$$
其中$\mathbf{\Psi }$ 就是转换基，$\mathbf{s}$是在频域空间的采样值，$\mathbf{\Psi }\mathbf{s}$也就将频域的采样值转化到时域中来。

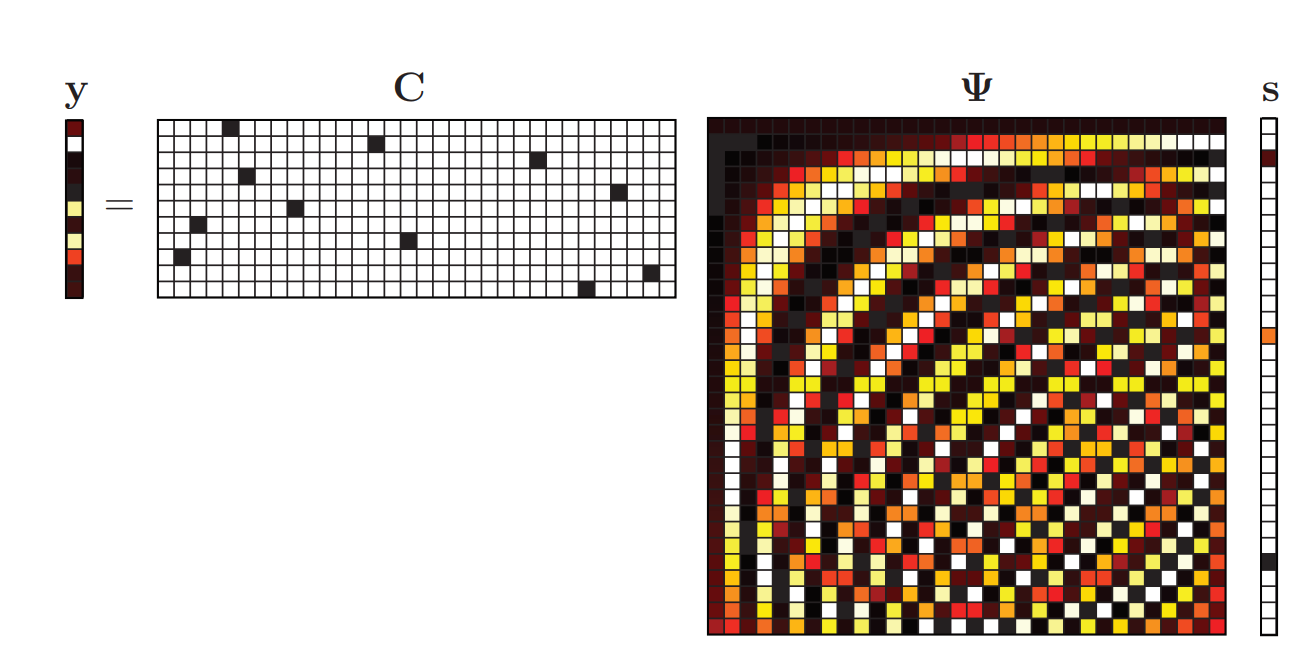
于是乎只要解出$\mathbf{s}$便可以得到时域中的稀疏采样值，那么如何解出$\mathbf{s}$呢？

答案是凸优化最小化算法：
$$\hat{\mathbf{s}}=\underset{\mathbf{s}}{\mathrm{argmin}}\Vert \mathbf{s}{\Vert }_1\text{ subject to }\mathbf{y}=\mathbf{C}\mathbf{\Psi }\mathbf{s}$$
上述问题的表述是，解出拥有最小第一范数值的 $\mathbf{s}$,且该$\mathbf{s}$满足 $\mathbf{y}=\mathbf{C}\mathbf{\Psi }\mathbf{s}$ 。

第一范数：
$$\Vert \mathbf{s}{\Vert }_1=\sum _{k=1}^n\left|s_k\right|$$
所以只要解出来$s$,就可以直接得到压缩后的数据，但前提是要指定随机采样的数量$p$，也就是$\mathbf{\Theta }$的维度。

采样矩阵$\mathbf{C}$必须满足两个要求：

1. 采样矩阵 $\mathbf{C}$必须是非连贯的，这样其每一行就不与 $\mathbf{\Psi }$ 具有相关性 。

2. 采样数量$p$必须足够大，满足：
   $$p\approx \mathcal{O}(K\log (n/K))\approx k_{1}K\log (n/K)$$

$k_1$取决于采样矩阵 $\mathbf{C}$的不连贯性，$K$则是其稀疏性，以图像压缩举例，1024*768像素，保留%5的图像质量，$K=1024\times 768\times 0.05\approx 40000$

if we generate a linear system of equations at random, that has sufficiently many more unknowns than knowns, then the resulting equations will have infinitely many solutions with high probability

如果随机产生的线性系统里有更多的未知量，那么解这个线性系统所建立的方程将会有很高的概率存在无穷多个解 。

Restricted isometry property 有限距离性质

When measurements are incoherent, the matrix $\mathbf{C}\mathbf{\Psi }$ satisfies a restricted isometry property
(RIP) for sparse vectors $s$

当采样值是非连续的，$\mathbf{C}\mathbf{\Psi }$ 满足RIP性质：
$$\left(1-{\delta }_K\right)\Vert \mathbf{s}{\Vert }_2^2\le \Vert \mathbf{C}\mathbf{\Psi }\mathbf{s}{\Vert }_2^2\le \left(1+{\delta }_K\right)\Vert \mathbf{s}{\Vert }_2^2$$
${\delta }_k$定义为对所有的$K$满足上述不等式的最小值，这个值随着样本$\mathbf{s}$的样本数量$p$而改变，$p$越大${\delta }_k$越小。

这个性质就保证了，存在一个界值${\delta }_k$，在足够多的非连续性取样的前提下，能够保证对不是噪音的数据进行准确恢复。另外从能量的角度来看，二范数一般代表能量，把上式子拆开看，$\mathbf{C}\mathbf{\Psi }$ 当成$\mathbf{s}$的系数，就相当于限定了$\mathbf{s}$的能量的一个范围，而这个范围随着$\mathbf{s}$的样本数量$p$而改变，数量越多这个范围就越精确，从而也就能够更加准确地进行数据的恢复和重建。

RIP参考：

1. R. G. Baraniuk. Compressive sensing. IEEE Signal Processing Magazine, 24(4):118–120,
   2007
2. E. J. Candès and M. B. Wakin. An introduction to compressive sampling. IEEE Signal
   Processing Magazine, pages 21–30, 2008.

使用一阶范数进行回归

一阶范数对一些干扰点具有较强的拒绝作用，引用一个例子做说明:

% Compressed Sensing Examples
% Copyright 2016, All Rights Reserved
% Code by Steven L. Brunton (sbrunton@uw.edu)

% Download and install CVX to run this example: http://cvxr.com/cvx/download/

clear all, close all, clc

x = sort(4*(rand(25,1)-.5)); % Random data from [-2,2]
b = .9*x + .1*randn(size(x)); % Line y=.9x with noise 
atrue = x\b;          % Least-squares slope (no outliers)

b(end) = -5.5;                  % Introduce outlier                 
acorrupt = x\b;                 % New slope

cvx_begin;       % L1 optimization to reject outlier
    variable aL1;     % aL1 is slope to be optimized 
    minimize( norm(aL1*x-b,1) );     % aL1 is robust
cvx_end;

hold on
scatter(x(1:end-1),b(1:end-1),'bo') % Data
scatter(x(end),b(end),'ro')         % Outlier
xgrid = -2:.01:2;
plot(xgrid,xgrid*atrue,'k')       % L2 fit (no outlier)
plot(xgrid,xgrid*acorrupt,'r--')    % L2 fit (outlier)
plot(xgrid,xgrid*aL1,'b--')         % L1 fit
axis([-2 2 -6 2])

结果:

上图中红线是使用二阶范数对数据做的拟合，可以发现，当把最后一个点b(end) = -5.5设置成和其他点偏离比较大的时候则对拟合直线坡度的影像很大。

而蓝线是用一阶范数解求得的拟合坡度aL1，发现这个最后的点对其影像很小，黑线是不带红色干扰点的最佳拟合坡度，如果去掉干扰点，则三线基本重叠：

LASSO 回归

LASSO（least absolute shrinkage and selection operator ）使用一阶数据抵抗数据的过拟合作用。一般数据集训练会采用交叉验证的方式，也就是使用80%的样本作为训练集20%样本作为测试集，然后进行多次重选样本集和测试集来训练模型，LASSO对于overdetermined问题的回归效果最好。

LASSO拟合：
$$\mathbf{x}=\underset{{\mathbf{x}}^{\prime }}{\mathrm{argmin}}{\Vert \mathbf{A}{\mathbf{x}}^{\prime }-\mathbf{b}\Vert }_2+\lambda \Vert \mathbf{x}{\Vert }_1$$
假设有一个矩阵$\mathbf{A}\in {\mathbb{R}}^{100\times 10}$ 代表系统, 然后我们有一部分对系统的输入的观测值 $x$，假设$x=[0;0;1;0;0;0;-1;0;0;0],(x\in {\mathbb{R}}^{10\times 1})$,以及系统所产生的所有的结果$b,b\in {\mathbb{R}}^{100\times 1}$，由于系统具有噪音，所以即便我们的输入只有一部分，系统的输出$b$依然全部都有值。

则整个系统可以表示为：
$$\mathbf{A}\mathbf{x}=\mathbf{b}$$
如果使用二阶范数进行拟合，即最小平方距离，我们可以直接计算$A^{-1}b$ 来得到 $x$, 然后看是否能得到正确的结果（现实世界中你不知道$x$是什么，只知道系统$A$和结果$b$，由于存在噪音，即便$x$全部为0，$b$ 依然会有值。而且即便我们使$x$不全为0，由于噪音的存在，我们也无法判断哪些是输入造成的输出，哪些是$x$通过系统得到的输出，也就没办法判断$A$中各行各部分是如何作用到$b$的）。

直接使用最小平方拟合出$x$:

发现每个$x$都有值，也就是说每个$b$的输出都关联着噪音的输入，无法判断$A$中哪部分作用了$x$ 。

使用Lasso拟合：

发现得到的$x$就和真实输入一样的位置有值，噪音作用被滤掉了。

clear all, close all, clc

A = randn(100,10);                   % Matrix of possible predictors
x = [0; 0; 1; 0; 0; 0; -1; 0; 0; 0]; % Two nonzero predictors
b = A*x + 2*randn(100,1);            % Observations (with noise)

xL2 = pinv(A)*b

[XL1 FitInfo] = lasso(A,b,'CV',10);
lassoPlot(XL1,FitInfo,'PlotType','CV')
lassoPlot(XL1,FitInfo,'PlotType','Lambda')

xL1 = XL1(:,FitInfo.Index1SE)
xL1DeBiased = pinv(A(:,abs(xL1)>0))*b