深度探索：强化学习中稳定高效的连续动作空间策略优化算法TD3原理及其应用

最新推荐文章于 2025-03-06 10:51:25 发布

生瓜蛋子

最新推荐文章于 2025-03-06 10:51:25 发布

阅读量2.7k

点赞数 32

分类专栏：机器学习文章标签：算法

本文链接：https://blog.csdn.net/qq_51320133/article/details/137711101

版权

机器学习专栏收录该内容

154 篇文章

订阅专栏

本文详细介绍了TD3算法，一种为解决连续动作空间问题而设计的强化学习方法，通过双Q网络、目标网络和延迟策略改进了DDPG，提升了学习性能和稳定性。文章覆盖了理论基础、实现细节、优缺点分析以及与其他算法的对比，展示了TD3在机器人控制、自动驾驶等领域的应用潜力。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1. 引言与背景

强化学习（Reinforcement Learning, RL）旨在通过智能体与环境的交互学习最优行为策略。在连续动作空间问题中，智能体需要在无穷多的可能动作中做出选择，这对传统RL算法提出了挑战。尤其是对于复杂的高维环境，如机器人控制、自动驾驶等，直接应用如DQN、REINFORCE等算法往往会导致学习不稳定、收敛缓慢甚至发散。为解决这些问题，研究人员提出了Twin Delayed Deep Deterministic Policy Gradients（TD3）算法，它在Deep Deterministic Policy Gradient（DDPG）的基础上，通过引入一系列创新技术，显著提高了在连续动作空间问题中的学习性能和稳定性。本文将详细介绍TD3的理论基础、算法原理、实现细节、优缺点分析、应用案例、与其他算法的对比，以及对该领域的未来展望。

2. TD3定理

TD3算法的理论基础与DDPG相同，基于确定性策略梯度定理（Deterministic Policy Gradient Theorem），该定理描述了如何直接对确定性策略进行梯度更新以最大化期望回报：

Theorem 1 (Deterministic Policy Gradient Theorem): 给定一个确定性策略π(·|s; θ)参数化为θ，其期望回报J(θ)的梯度可以通过下式计算：

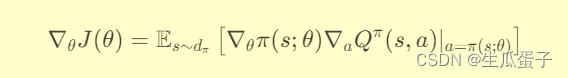
其中，dπ是π诱导的状态分布，Qπ(s, a)是状态s下执行动作a的Q函数。

TD3算法的核心改进在于通过双Q网络、目标网络和延迟更新策略等技术，有效地减小了Q值估计的偏差，从而优化了策略梯度的计算。

3. 算法原理

TD3遵循以下主要步骤：

Step 1: 初始化两个Q网络Q1和Q2（共享参数），以及两个策略网络π和π'（目标网络，参数定期软更新）。

Step 2: 通过ε-greedy策略（或噪声扰动）根据π选择动作，与环境交互，收集经验（s, a, r, s', done）。

Step 3: 将经验存储在回放缓冲区中，并定期从中采样批次数据进行学习。

Step 4: 更新Q网络：

从回放缓冲区采样一批数据，计算每个样本的最小Q值估计min(Q1(s', a'), Q2(s', a'))，其中a' = π'(s')。
计算目标Q值y = r + γ(1 - done) * min(Q1(s', a'), Q2(s', a'))。
以(y - Q1(s, a))^2作为损失函数，更新Q1网络参数。同理更新Q2网络参数。

Step 5: 更新策略网络：

从回放缓冲区采样一批数据，计算每个样本的策略梯度∇θJ(θ)，使用clip(a - π(s; θ), -η, η) + π(s; θ)对梯度进行截断。
使用截断后的梯度更新π网络参数。每两次Q网络更新后更新一次策略网络。

Step 6: 定期（如每隔固定步数）将π的参数软更新到π'，保持目标网络的稳定性。

4. 算法实现

以下是一个使用PyTorch实现TD3算法的简单示例（以MuJoCo环境为例）：

Python

import torch
import torch.nn as nn
import torch.optim as optim
import gym
import numpy as np

class Actor(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(Actor, self).__init__()
        self.l1 = nn.Linear(state_dim, hidden_dim)
        self.l2 = nn.Linear(hidden_dim, hidden_dim)
        self.l3 = nn.Linear(hidden_dim, action_dim)

    def forward(self, state):
        x = torch.relu(self.l1(state))
        x = torch.relu(self.l2(x))
        return torch.tanh(self.l3(x))

class Critic(nn.Module):
    def __init__(self, state_dim, action_dim, hidden_dim=256):
        super(Critic, self).__init__()
        self.l1 = nn.Linear(state_dim + action_dim, hidden_dim)
        self.l2 = nn.Linear(hidden_dim, hidden_dim)
        self.l3 = nn.Linear(hidden_dim, 1)

    def forward(self, state, action):
        x = torch.cat([state, action], dim=-1)
        x = torch.relu(self.l1(x))
        x = torch.relu(self.l2(x))
        return self.l3(x)

class TD3Agent:
    def __init__(self, env, gamma=0.99, tau=0.005, policy_noise=0.2, noise_clip=0.5, policy_freq=2):
        self.env = env
        self.gamma = gamma
        self.tau = tau
        self.policy_noise = policy_noise
        self.noise_clip = noise_clip
        self.policy_freq = policy_freq

        self.actor = Actor(env.observation_space.shape[0], env.action_space.shape[0]).to(device)
        self.actor_target = Actor(env.observation_space.shape[0], env.action_space.shape[0]).to(device)
        self.critic_1 = Critic(env.observation_space.shape[0], env.action_space.shape[0]).to(device)
        self.critic_1_target = Critic(env.observation_space.shape[0], env.action_space.shape[0]).to(device)
        self.critic_2 = Critic(env.observation_space.shape[0], env.action_space.shape[0]).to(device)
        self.critic_2_target = Critic(env.observation_space.shape[0], env.action_space.shape[0]).to(device)

        self.actor_optimizer = optim.Adam(self.actor.parameters(), lr=3e-4)
        self.critic_1_optimizer = optim.Adam(self.critic_1.parameters(), lr=3e-4)
        self.critic_2_optimizer = optim.Adam(self.critic_2.parameters(), lr=3e-4)

        self.replay_buffer = ReplayBuffer()

    def select_action(self, state):
        state = torch.FloatTensor(state.reshape(1, -1)).to(device)
        return self.actor(state).cpu().data.numpy().flatten()

    def learn(self, batch_size=100):
        state, action, next_state, reward, done = self.replay_buffer.sample(batch_size)

        state = torch.FloatTensor(state).to(device)
        action = torch.FloatTensor(action).to(device)
        next_state = torch.FloatTensor(next_state).to(device)
        reward = torch.FloatTensor(reward).unsqueeze(1).to(device)
        done = torch.FloatTensor(np.float32(done)).unsqueeze(1).to(device)

        noise = torch.FloatTensor(action.size()).normal_(0, self.policy_noise).to(device)
        noise = noise.clamp(-self.noise_clip, self.noise_clip)

        next_action = (self.actor_target(next_state) + noise).clamp(-1, 1)
        target_Q1 = self.critic_1_target(next_state, next_action)
        target_Q2 = self.critic_2_target(next_state, next_action)
        target_Q = torch.min(target_Q1, target_Q2)
        target_Q = reward + (1 - done) * self.gamma * target_Q

        current_Q1 = self.critic_1(state, action)
        current_Q2 = self.critic_2(state, action)

        critic_loss = F.mse_loss(current_Q1, target_Q) + F.mse_loss(current_Q2, target_Q)
        self.critic_1_optimizer.zero_grad()
        self.critic_2_optimizer.zero_grad()
        critic_loss.backward()
        self.critic_1_optimizer.step()
        self.critic_2_optimizer.step()

        if self.total_it % self.policy_freq == 0:
            actor_loss = -self.critic_1(state, self.actor(state)).mean()
            self.actor_optimizer.zero_grad()
            actor_loss.backward()
            self.actor_optimizer.step()

            self.soft_update(self.critic_1_target, self.critic_1, self.tau)
            self.soft_update(self.critic_2_target, self.critic_2, self.tau)
            self.soft_update(self.actor_target, self.actor, self.tau)

    def soft_update(self, target_net, eval_net, tau):
        for target_param, local_param in zip(target_net.parameters(), eval_net.parameters()):
            target_param.data.copy_(tau * local_param.data + (1.0 - tau) * target_param.data)

    def train(self, num_episodes=1000):
        for episode in range(num_episodes):
            state = self.env.reset()
            episode_reward = 0
            done = False
            while not done:
                action = self.select_action(state)
                next_state, reward, done, _ = self.env.step(action)
                self.replay_buffer.add(state, action, next_state, reward, done)
                state = next_state
                episode_reward += reward

                if len(self.replay_buffer) > batch_size:
                    self.learn()

            print(f"Episode {episode}, Reward: {episode_reward:.3f}")

if __name__ == '__main__':
    device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
    env = gym.make('Pendulum-v0')
    agent = TD3Agent(env)
    agent.train()

这段代码实现了基于PyTorch框架的TD3（Twin Delayed Deep Deterministic Policy Gradients）算法，用于解决连续动作空间的强化学习问题。主要分为以下四个部分：

网络结构定义：定义了Actor（策略网络）和Critic（价值网络）两个类，分别用于生成策略动作和评估状态-动作对的价值。Actor网络包含三个全连接层，通过ReLU激活函数进行非线性变换，输出层使用tanh激活函数确保生成的动作限制在[-1, 1]范围内。Critic网络接受状态和动作作为输入，将其拼接并通过三个全连接层处理，同样使用ReLU激活函数，输出单个标量Q值。
TD3Agent类：定义了一个名为TD3Agent的类，封装了TD3算法的主体逻辑。该类包含环境对象、策略网络（Actor及目标网络）、价值网络（两个Critic及对应目标网络）、优化器（Adam算法）以及经验回放缓冲区。类中实现了select_action方法，根据当前状态通过策略网络选择动作；learn方法从经验回放缓冲区采样经验，计算目标Q值，更新价值网络参数，并在满足条件时同步至目标网络及更新策略网络；以及train方法，用于进行多轮训练并在每轮结束后打印奖励。
ReplayBuffer类：虽然未在给出的代码片段中直接展示，但根据TD3Agent类中的replay_buffer属性和learn方法的使用，可知存在一个ReplayBuffer类，用于存储智能体与环境交互产生的经验（状态、动作、奖励、新状态、是否结束），并支持从中随机采样一批经验。
主程序：在__main__块中，首先创建环境（使用Pendulum-v0），判断是否使用GPU设备，然后初始化一个TD3Agent对象，并调用其train方法进行训练。在训练过程中，智能体与环境进行多轮交互，积累经验并进行学习，最终学会在给定环境中执行有效的策略，以获得较高的累积奖励。

综上，这段代码构建了一个完整的TD3算法实现，利用PyTorch框架进行深度学习模型的搭建、训练与优化，适用于解决连续动作空间的强化学习任务。

5. 优缺点分析

优点：

双Q网络：通过使用两个Q网络评估动作价值，取其最小值作为目标Q值，有效减少了Q值过估计，提高了学习稳定性。
目标网络：使用目标网络稳定Q值估计，避免了频繁更新导致的Q值波动。
延迟策略更新：每两次Q网络更新后才更新一次策略网络，进一步减小了策略与价值函数之间的耦合，有利于稳定学习过程。
动作噪声：在策略网络输出的动作上加入噪声扰动，促进探索并防止策略过早收敛到局部最优。

缺点：

计算资源需求：使用双Q网络和目标网络增加了模型复杂度和计算成本。
超参数敏感：TD3对超参数（如τ、η、policy_noise等）较为敏感，需要精心调整以获得良好性能。
收敛速度：由于引入了额外的稳定化措施，TD3的收敛速度可能略慢于某些更激进的算法。

6. 案例应用

机器人控制：在MuJoCo、PyBullet等模拟环境中，TD3成功应用于各种机器人（如Ant、Humanoid、Fetch等）的运动控制任务，学习到了复杂、高效的动作策略。

自动驾驶：在自动驾驶模拟器中，TD3被用于优化车辆的转向、加减速等控制策略，实现安全、高效的路径跟踪。

能源管理系统：在智能电网、数据中心等能源管理系统中，TD3被用于优化能源分配、负载调度等决策问题，实现能源效率与服务质量的平衡。

7. 对比与其他算法

与DDPG：TD3是DDPG的改进版本，通过引入双Q网络、目标网络、延迟更新策略和动作噪声等技术，显著提高了学习稳定性，降低了Q值过估计，从而在连续动作空间问题中表现出更好的性能。

与SAC（Soft Actor-Critic）：SAC是一种基于最大熵原理的强化学习算法，通过最大化预期回报与策略熵之和来鼓励探索。相比TD3，SAC在某些任务中可能具有更快的收敛速度和更好的探索能力，但计算复杂度更高，对超参数调整的要求也更为严格。

与PPO（Proximal Policy Optimization）：PPO是一种基于策略梯度的算法，通过限制策略更新的幅度来保证稳定性。与TD3相比，PPO在某些任务中可能具有更快的收敛速度和更好的样本效率，但对环境模型的假设较少，适用于更广泛的强化学习问题。

8. 结论与展望

TD3作为连续动作空间强化学习的重要算法，通过一系列创新技术有效解决了Q值过估计、学习不稳定等问题，展现出在复杂机器人控制、自动驾驶等领域优秀的学习性能和稳定性。尽管存在计算资源需求较高、超参数敏感等挑战，但随着硬件性能的提升和算法优化技术的进步，TD3及其变种有望在更多实际应用中发挥关键作用。

未来，TD3的研究与应用可以从以下几个方向展开：

算法优化：进一步探索如何优化TD3的网络架构、优化方法、正则化技术等，提高其收敛速度、稳定性和泛化能力。
环境适应性：研究如何在未知、动态、部分可观测或非马尔科夫环境中有效地应用TD3，或者针对特定领域的任务（如复杂机器人操作、能源管理等）定制化设计TD3模型。
理论深化：深入研究TD3的学习过程和收敛性质，为算法设计与调优提供理论指导，同时探索TD3与其它强化学习框架（如 actor-critic、蒙特卡洛方法等）的融合与比较。
实际应用推广：推动TD3在更多实际场景中的落地应用，如工业自动化、能源管理、医疗决策、金融交易等，结合具体领域的知识，设计针对性的环境建模、状态表示、奖励函数等，同时考虑现实约束（如延迟、通信成本、安全性等）对算法设计的影响。