深度探索：机器学习中的最大似然估计（MLE）原理及其应用

目录

1. 引言与背景

2. 最大似然定理

3. 算法原理

4. 算法实现

5. 优缺点分析

优点：

缺点：

6. 案例应用

7. 对比与其他算法

8. 结论与展望

---

1. 引言与背景

在机器学习领域，统计推断是建立和评估模型的核心方法之一。其中，最大似然估计（Maximum Likelihood Estimation, MLE）作为一项基础且广泛应用的参数估计技术，凭借其直观的原理、坚实的理论基础以及良好的实践效果，成为众多统计模型构建过程中的首选策略。本文旨在系统地阐述最大似然估计的理论基础、算法原理、实现细节、优缺点分析、实际应用案例，并将其与相关算法进行对比，最后展望其在机器学习未来发展的潜在影响。

2. 最大似然定理

最大似然定理是最大似然估计的理论基石。该定理指出，对于一个给定的观测数据集和一个参数化的概率模型，若模型参数的真值未知，那么在所有可能的参数值中，使观测数据出现的概率（即似然函数）最大的那个参数值，可以作为参数的估计值。简而言之，最大似然估计旨在找到能使已知数据最“自然”、最“合理”的模型参数。

数学上，假设数据集 是独立同分布的样本，其共同的概率分布由参数向量 θ 决定。则似然函数 可以表示为所有样本联合发生的概率：

最大似然估计的目标就是找到使似然函数最大化的参数值，即：

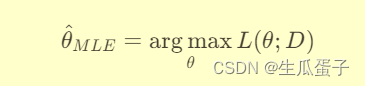
或者等价地最大化对数似然函数（为了计算方便，避免数值下溢）：

3. 算法原理

最大似然估计的算法原理主要涉及以下几个步骤：

步骤一：确定模型与似然函数：首先，根据问题背景选择一个合适的概率模型，如高斯分布、伯努利分布、多项式分布等。然后，根据选定的模型形式写出对应的似然函数。

步骤二：求解最大似然估计：通常，直接最大化似然函数或对数似然函数可能会遇到非凸、无解析解等问题。此时，可以借助数值优化方法，如梯度上升法、牛顿法、拟牛顿法或现代优化算法（如L-BFGS、Adam等），通过迭代寻找使对数似然函数最大化的参数值。

步骤三：评估与验证：获得最大似然估计参数后，需对其进行评估，如计算预测误差、交叉验证等，确保所选参数能有效拟合数据并具有良好的泛化能力。

4. 算法实现

下面我将详细讲解如何使用Python实现一个简单的最大似然估计（MLE）示例，以拟合一个正态分布（高斯分布）为例。我们将从数据生成、定义似然函数、实现MLE算法以及可视化结果等步骤进行说明。

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import minimize

# 1. 数据生成
np.random.seed(42)  # 设置随机种子以保证结果可复现
true_mu = 5.0  # 真实均值
true_sigma = 1.5  # 真实标准差
sample_size = 100  # 样本数量
data = np.random.normal(true_mu, true_sigma, sample_size)  # 生成正态分布数据

# 2. 定义似然函数
def likelihood(theta, data):
    mu, sigma = theta  # 解包参数
    n = len(data)
    log_likelihood = -n/2 * np.log(2*np.pi*sigma**2) - (1/(2*sigma**2)) * np.sum((data-mu)**2)
    return -log_likelihood  # 返回负对数似然函数，因为minimize函数需要最小化目标

# 3. 实现MLE算法
initial_guess = [0, 1]  # 初始参数猜测
result = minimize(likelihood, initial_guess, args=(data,), method='Nelder-Mead')

# 4. 获取并打印MLE估计的参数
mu_mle, sigma_mle = result.x
print(f"MLE estimated mean: {mu_mle:.2f}, true mean: {true_mu}")
print(f"MLE estimated std dev: {sigma_mle:.2f}, true std dev: {true_sigma}")

# 5. 可视化结果
plt.figure(figsize=(10, 6))
sns.histplot(data, kde=True, color="skyblue", label="Data")
x_range = np.linspace(np.min(data), np.max(data), 1000)
plt.plot(x_range, norm.pdf(x_range, mu_mle, sigma_mle), label="MLE Fit")
plt.axvline(true_mu, linestyle="--", color="red", label="True Mean")
plt.axvline(mu_mle, linestyle="--", color="green", label="Estimated Mean")
plt.legend()
plt.title("Maximum Likelihood Estimation for a Normal Distribution")
plt.show()

代码详解：

1. 数据生成

我们使用numpy.random.normal()函数生成一个正态分布的数据集，指定真实的均值true_mu、标准差true_sigma以及样本数量sample_size。

2. 定义似然函数

定义一个名为likelihood的函数，它接受参数向量theta（包含待估计的均值mu和标准差sigma）及数据集data。函数内部计算负对数似然函数（因为在scipy.optimize.minimize中，我们需要提供一个可最小化的函数）。正态分布的对数似然函数公式如下：

3. 实现MLE算法

使用scipy.optimize.minimize函数来执行最大似然估计。我们指定使用Nelder-Mead优化方法（一种无需梯度的数值优化算法），初始猜测参数为initial_guess，目标函数为之前定义的likelihood函数，并传入实际数据集data作为额外参数。

4. 获取并打印MLE估计的参数

从优化结果result中提取出最大似然估计的均值和标准差，并与真实的均值和标准差进行比较。

5. 可视化结果

利用matplotlib和seaborn库绘制数据直方图，并在其上叠加MLE拟合的正态分布曲线，以及真实均值和估计均值的垂直参考线，以便直观地对比数据分布、MLE估计效果以及真实参数值。

运行上述代码，您将看到MLE估计的结果以及数据分布与MLE拟合曲线的可视化展示。通过比较估计参数与真实参数，可以评估MLE方法的有效性。在这个例子中，由于正态分布的MLE有解析解，所以估计结果应当非常接近真实值。在实际应用中，可能会遇到更复杂的模型，这时MLE通常需要依赖数值优化方法来求解。

5. 优缺点分析

优点：

• 理论基础坚实：最大似然估计基于强大的统计学理论，有明确的数学解释和推导过程。
• 易于理解与实现：直观地寻找使数据出现可能性最大的参数，算法实现相对简单。
• 适用范围广：适用于各类概率模型，包括参数型和非参数型模型。
• 可扩展性强：可以自然地推广到贝叶斯框架下的最大后验概率估计（MAP）。

缺点：

• 对模型假设敏感：如果所选模型与真实数据生成过程不匹配，可能导致较差的估计效果。
• 易受异常值影响：由于最大化的是所有观测值的联合概率，个别极端值可能显著影响估计结果。
• 可能存在局部最优解：对于复杂的似然函数，数值优化方法可能陷入局部最优而非全局最优。
• 未考虑模型不确定性：仅提供单点估计，未提供参数的不确定性信息（如置信区间）。

6. 案例应用

最大似然估计在诸多机器学习任务中发挥着关键作用，以下是一些典型应用案例：

• 线性回归：通过最大化数据点到回归直线的联合概率，求得最优的截距和斜率。
• 逻辑回归：用于分类任务，通过最大化数据点按类标记的概率，得到分类边界。
• 高斯混合模型（GMM）：用于聚类，通过最大化数据点属于各个高斯分量的概率总和，确定分量的参数。
• 隐马尔可夫模型（HMM）：在语音识别、生物信息学等领域，通过最大化观察序列和隐藏状态序列联合概率，估计模型参数。

7. 对比与其他算法

与最小二乘法对比：最小二乘法主要用于线性模型参数估计，侧重于最小化预测误差的平方和，而最大似然估计则从概率角度最大化数据的联合概率。两者在简单线性回归问题上结果一致，但在更复杂模型或非高斯噪声情况下，最大似然估计往往更具一般性和解释力。

与贝叶斯估计对比：最大似然估计是频率派统计的方法，只关注参数的点估计；而贝叶斯估计结合了先验知识，提供参数的全概率分布。最大后验概率估计（MAP）是最大似然估计与贝叶斯估计的结合，既考虑了数据又考虑了先验。

8. 结论与展望

最大似然估计作为统计推断的核心方法，在机器学习领域具有广泛的应用价值和深远影响。尽管存在对模型假设敏感、易受异常值影响等局限性，但其直观的原理、坚实的理论基础以及高效的实现方式使其在实践中仍占据主导地位。随着深度学习、强化学习等新兴领域的快速发展，最大似然估计将继续演化并适应新的模型结构与优化框架。同时，结合现代优化算法、并行计算技术以及贝叶斯方法的融合，最大似然估计有望在保持其核心优势的同时，进一步提升参数估计的准确性和鲁棒性，为未来的机器学习研究与应用开辟更广阔的道路。