深度探索：机器学习中的Metropolis-Hastings原理及其应用

最新推荐文章于 2024-12-20 17:07:51 发布

生瓜蛋子

最新推荐文章于 2024-12-20 17:07:51 发布

阅读量3.2k

点赞数 30

分类专栏：机器学习文章标签：机器学习人工智能

本文链接：https://blog.csdn.net/qq_51320133/article/details/137953262

版权

机器学习专栏收录该内容

154 篇文章

订阅专栏

1.引言与背景

2.Metropolis-Hastings定理

1.引言与背景

在大数据时代，机器学习作为一门核心学科，致力于从海量数据中提取有价值的信息和知识。其中，采样方法在模型训练、参数估计、概率分布探索等众多领域扮演着关键角色。在众多采样技术中，Metropolis-Hastings(MH)算法以其强大的通用性和高效性，成为统计推断和机器学习研究中的重要工具。本文将对Metropolis-Hastings算法进行全面探讨，包括其理论基础、工作原理、实现细节、优缺点分析、实际应用案例、与其他算法的对比以及未来展望。

2.Metropolis-Hastings定理

Metropolis-Hastings定理是该算法的核心理论基石，基于马尔科夫链蒙特卡洛（Markov Chain Monte Carlo, MCMC）方法。该定理指出，对于任意的概率分布π(x)，只要设计出一个合适的马尔科夫链转移核Q(x'|x)，使得满足详细的平衡条件：

即可保证该马尔科夫链的平稳分布为π(x)。这意味着，经过足够长的时间，链上采样的点将按照目标分布π(x)进行分布，从而实现从难以直接采样的复杂分布中抽样。

3.算法原理

Metropolis-Hastings算法遵循以下四个基本步骤：

初始化：选择一个初始状态x^(0)。
提议生成：根据当前状态x^(t)，生成一个候选新状态x'，通常通过一个简单且易于采样的提议分布q(x'|x^(t))实现。
接受/拒绝判定：计算接受概率α(x^(t), x')：

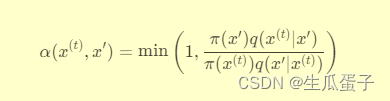
这个比例反映了新旧状态在目标分布π(x)下的相对权重以及提议分布的逆向移动概率。
状态更新：以接受概率α随机决定是否接受候选新状态。若接受（如通过抛硬币决定），则令x^(t+1)=x'；否则保持原状态，即x^(t+1)=x^(t)。重复上述过程直至达到所需的迭代次数或收敛标准。

4.算法实现

Metropolis-Hastings算法的实现涉及以下几个关键环节：

提议分布的选择：应确保提议分布既不太集中以至于难以逃离局部极值，也不太分散导致接受率过低。常用的提议分布包括高斯分布、均匀分布、多峰分布等，也可结合领域知识设计自适应提议分布。
调整超参数：如提议分布的标准差、步长等，以优化接受率和采样效率。常用的方法包括模拟退火、窗口调整、自适应MCMC等。
收敛诊断：通过观察链长、嵌入维数、有效样本大小、 Gelman-Rubin统计量等指标判断算法是否已收敛到目标分布。
后处理：对得到的马尔科夫链样本进行去相关处理，如使用截尾、薄化、阻尼等方法，以减少序列相关性并提高样本的有效性。

以下是一个使用Python实现Metropolis-Hastings算法的示例代码，并配以详细讲解：

Python

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import norm

# 目标分布：双峰高斯混合分布
def target_distribution(x):
    # 分布参数：两个高斯均值、方差及混合比例
    mu1, mu2, sigma1, sigma2, w1, w2 = -2, 2, 1, 1, 0.½, 0.½
    return w1 * norm.pdf(x, loc=mu1, scale=sigma1) + w2 * norm.pdf(x, loc=mu2, scale=sigma2)

# 提议分布：对称高斯分布
def proposal_distribution(x, current_state, std_dev):
    return norm.pdf(x, loc=current_state, scale=std_dev)

# Metropolis-Hastings算法
def metropolis_hastings(target_dist, proposal_dist, num_samples, initial_state, std_dev, burn_in=0):
    samples = [initial_state]
    current_state = initial_state

    for _ in range(num_samples):
        # 提议新的状态
        proposed_state = np.random.normal(current_state, std_dev)

        # 计算接受概率
        acceptance_ratio = min(1, target_dist(proposed_state) / target_dist(current_state))

        # 随机决定是否接受提议
        if np.random.uniform(0, 1) <= acceptance_ratio:
            current_state = proposed_state

        # 添加当前状态到样本列表
        samples.append(current_state)

    # 去除“烧瓶期”样本
    samples = samples[burn_in:]

    return samples

# 参数设置
num_samples = 10000  # 总样本数
burn_in = 2000       # 烧瓶期长度
initial_state = 0     # 初始状态
std_dev = 1          # 提议分布标准差

# 运行Metropolis-Hastings算法
mh_samples = metropolis_hastings(target_distribution, proposal_distribution, num_samples, initial_state, std_dev, burn_in)

# 可视化结果
plt.hist(mh_samples, bins=50, density=True, alpha=0.5)
x_range = np.linspace(-5, 5, 1000)
plt.plot(x_range, target_distribution(x_range), label='True Distribution', linewidth=2)
plt.legend()
plt.show()

代码讲解：

定义目标分布：这里我们选择一个双峰高斯混合分布作为示例目标分布。实际应用中，目标分布可能由模型的后验概率或其他难以直接采样的概率密度函数构成。
定义提议分布：选用对称高斯分布作为提议分布，它以当前状态为中心，具有固定标准差std_dev。实际应用中，提议分布的选择需依据目标分布的特点进行调整，以确保较好的采样效率。
Metropolis-Hastings算法实现：
- metropolis_hastings函数接收目标分布、提议分布、样本总数、初始状态、提议分布的标准差以及可选的烧瓶期长度（burn_in）作为参数。
- 在循环中，每一步：
  - 从提议分布中生成一个新的状态proposed_state。
  - 计算接受概率acceptance_ratio，即新旧状态在目标分布下的比例值，取其最小值1。
  - 生成一个[0, 1)之间的随机数，若小于接受概率，则接受新状态，否则保留当前状态。
  - 将当前状态添加到样本列表中。
- 完成循环后，去除烧瓶期内的样本，返回最终采样序列。
参数设置：指定所需采样的样本总数、初始状态、提议分布的标准差以及烧瓶期长度。
运行算法：调用metropolis_hastings函数，得到Metropolis-Hastings算法生成的样本序列。
结果可视化：绘制样本直方图并与目标分布曲线进行比较，验证算法的有效性。理想情况下，样本分布应与目标分布吻合。

通过这段代码，我们可以直观地看到Metropolis-Hastings算法如何从给定的目标分布中抽样，并通过可视化检查采样效果。在实际应用中，您需要根据具体问题替换目标分布和提议分布函数，并调整相关参数以获得最佳采样性能。

5.优缺点分析

优点：

通用性：Metropolis-Hastings算法适用于任何已知概率密度函数的采样问题，无需知道其显式形式，只需能评估其数值。
高效性：尽管单次迭代可能仅产生微小变化，但通过长时间运行，MH算法能够遍历整个状态空间，有效探索复杂分布。
并行化潜力：通过独立运行多个链或采用分层采样等技术，MH算法可方便地进行并行化加速。

缺点：

收敛速度：对于某些高度尖峰或多模态分布，MH算法可能需要较长的“烧瓶期”才能收敛，且容易陷入局部最优。
提议分布选择：提议分布的选择对算法性能影响显著，但往往需要领域专业知识和试错调整。
序列相关性：生成的样本之间存在较强的相关性，需进行后处理以提高样本独立性。

6.案例应用

Metropolis-Hastings算法在诸多机器学习场景中展现出广泛应用价值，例如：

贝叶斯推断：在复杂的后验分布下，MH算法用于从全贝叶斯模型中抽取参数样本，进行模型平均、不确定性量化等。
深度学习：在变分自编码器、生成对抗网络等模型的训练中，MH算法用于从隐变量分布中采样，辅助模型学习和生成任务。
统计物理：在伊辛模型、自旋玻璃等物理系统中，MH算法用于模拟系统动力学，探究相变、临界行为等现象。

7..对比与其他算法

与其他采样方法相比，Metropolis-Hastings算法有以下特点：

与Gibbs采样对比：Gibbs采样适用于条件概率已知且易于采样的情况，每次只更新一个变量，降低了接受率问题，但不适用于高维、强耦合的系统。
与Hamiltonian Monte Carlo(HMC)：HMC引入物理系统的动力学模拟，利用动量变量跨越概率分布的高低区域，提高了采样效率，尤其适合处理高维、多模态分布，但实现较为复杂，对超参数调整敏感。

8.结论与展望

Metropolis-Hastings算法作为MCMC方法的代表，凭借其强大的通用性和在复杂分布采样中的出色表现，已成为机器学习、统计推断等领域不可或缺的工具。然而，面对大规模、高维度、强耦合的现代数据科学问题，如何进一步提升MH算法的采样效率、降低收敛时间、自动调整提议分布等，仍具有挑战性和研究价值。未来的研究方向可能包括：开发新型混合MH算法、融合深度学习进行智能提议分布学习、探索量子计算等新型计算平台上的MH算法实现等。随着这些研究的深入，我们有理由期待Metropolis-Hastings算法在解决更复杂、更前沿的机器学习问题中发挥更大作用。