Overall Accuracy（OA）、Average Accuracy（AAcc）计算公式

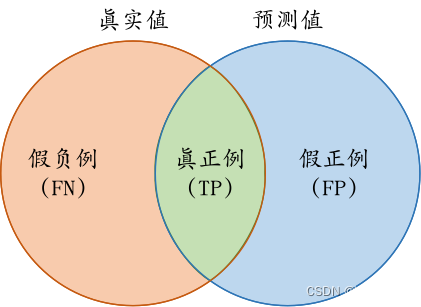
四个重要的指标：
True Positive（TP）、False Positive（FP）、True Negative（TN）和False Negative（FN）。
TP表示分类器预测结果为正样本，实际也为正样本，即正样本被正确识别的数量；
FP表示分类器预测结果为正样本，实际为负样本，即误报的负样本数量；
TN表示分类器预测结果为负样本，实际也为负样本，即负样本被正确识别的数量；
FN表示分类器预测结果为负样本，实际为正样本，即漏报的正样本数量。

---

以二分类为例：

1.总体精度(Overall Accuracy, OA)：样本中正确分类的总数除以样本总数。
OA=(TP+TN)/(TP+FN+FP+TN)

2.平均精度(Average Accuracy, AA)：每一类别中预测正确的数目除以该类总数，记为该类的精度，最后求每类精度的平均。
AA=(TP/(TP+FN)+TN/(FP+TN))/2

OA与Accuracy定义一致。AA与Recall计算公式比较一致，不过考虑了正负两例的计算。

---

 Accuracy、Precision、Recall以及F-score

1.准确率(Accuracy)：模型的精度，即模型预测正确的个数 / 样本的总个数;一般情况下，模型的精度越高，说明模型的效果越好。
Accuracy=(TP+TN)/(TP+TN+FP+FN) 

2.精确率(Precision)：模型预测为正的部分的正确率。
Precision=TP/(TP+FP) 

3.召回率(Recall)：真实值为正的部分，被模型预测出来且正确的比重。
Recall=TP/(TP+FN) 

4.F1-score：此指标综合了Precision与Recall的产出的结果，取值范围从0到1的，1代表模型的输出最好，0代表模型的输出结果最差。
F=2*Precision*Recall/(Precision+Recall)

---

IoU与MIoU

以二分类为例：

IoU(Intersection over Union，交并比)：计算某一类别预测结果和真实值的交集和并集的比值。计算公式如下：

MIoU(Mean Intersection over Union，平均交并比)：计算所有类别的IoU的平均值。计算公式如下（因k从0开始，故需要加1）：

计算二分类混淆矩阵中正负两类的MIoU MIoU=(IoU(正)+IoU(负))/2 =(TP/(FN+FP+TP)+TN/(TN+FN+FP))/2

多分类：

某一类的IoU的分子为：该类所在混淆矩阵对角线的值。

某一类的IoU的分母为：该类所在混淆矩阵对角线的位置对应的行和列的总和。（对角线位置的值只能计算一次）

---

因对于一个样本来说，FN+TP是固定的，那么IoU就可以变为IoU=TP/(K+FP)，那么主要相当于分析TP与FP的变化趋势。孤立的分析IoU，这里有4种情况可能使得IoU变大：

1）TP不变，FP减小；IoU肯定变大

2）TP变小，FP变小；IoU应该可大可小

3）TP变大，FP不变；IoU肯定变大

3）TP变大，FP变大；IoU应该可大可小！如下表格C1到C2，IC1=1/(1+5)=1/6、IC2=3/(4+5)=1/3；此时虽然IoU变大，但是Accuracy却变小了，模型的好坏需要另外讨论。

假设	TP	FN	FP	TN	Total
C1	1	4	1	4	10
C2	3	2	4	1	10
C3	2	3	2	3	10

也就是说IoU变大，模型不一定变好，但大多数情况下还是变好的。　

---

 混淆矩阵及相关精度指标计算和实现记录 - 他的博客 - 博客园 (cnblogs.com)