通俗易懂介绍傅里叶变换

开场白

最近在参加夏令营的时候，阅读到了CompGCN这篇文章，其中在计算两个序列相关性的时候，使用循环相关这一方法，但他并未使用的是时域的计算方法而是频域的计算方法来降低计算的复杂度，借此回顾了数字信号处理的相关知识，希望读这篇文章让大家对傅里叶变换有一个更广泛的认识同时感叹傅里叶同学的智慧，我将用尽可能理解语言来进行阐述，欢迎大家指正。

傅里叶变换

什么是频域?

我们生活在这个世界，好像一切事情都是沿着时间发展的，比如人的身高、大家的感情经历、股票趋势等等，大家对时域理解相比于频域更容易。但是我告诉你，如果这个世界从频域的角度考虑是静态的，你可能会不可思议，我先举一个例子，再写这篇笔记的时候，为了避免枯燥乏味，我打开了音乐，没错音乐他的播放是随时间，这个就是时域。

这是我们对音乐最普遍的理解，对于乐手来说他是由一个个音符组成的，其中不同的音符他的频率不同，这就是下图就是该音乐在频域的表现方式，大家对频域这一概念其实并不陌生。

时域：

频域：

所以在时域，钢琴的琴弦一上一下的摆动，在频域就是一个一个永恒的音符。因此，大家眼中看似眼花缭乱的世界，其实可能是上帝手中已经谱写好的一副音符。这并不是鸡汤，傅里叶同学已经为我们证明了，任何周期函数都可以看成是不同振幅、不同相位、正弦波叠加（这里的正弦波指的不仅是正弦还有余弦）。非周期函数也可以看成周期很大的周期函数，在频域和时域来回穿梭的通道，就是传说中的傅里叶分析，傅里叶分析包括傅里叶级数和傅里叶变换，让我们一步一步的深入。

傅里叶级数的频谱

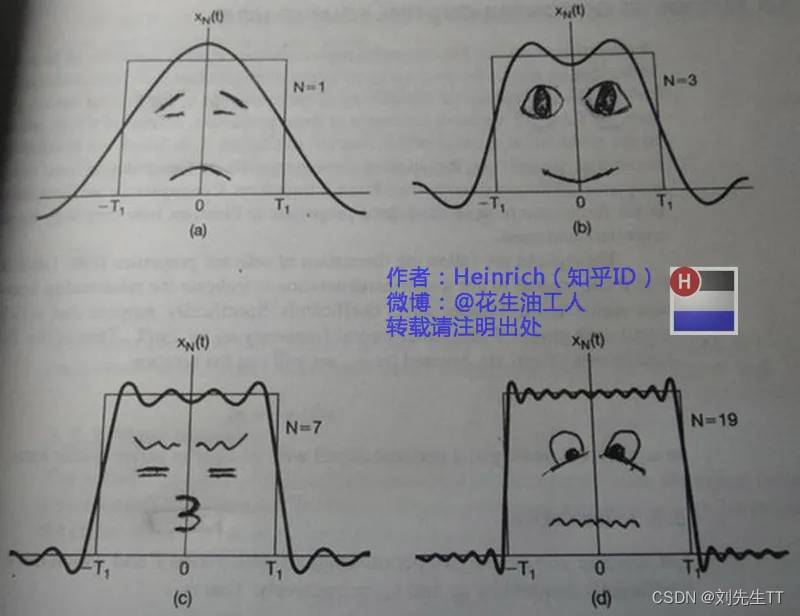
第一幅图是一个郁闷的正弦波 cos（x）
第二幅图是2个卖萌的正弦波的叠加cos(x)+a.cos(3x)
第三幅图是4个发春的正弦波的叠加
第四幅图是10个便秘的正弦波的叠加
可以发现，随着正弦波数量的增多，他们最终会形成一个矩形，所以大家只要肯努力，实干，没有什么是做不成的。随着正弦波数量的增加，所有正弦波中上升的部分让本来慢慢增加的曲线不断变陡，而上升部分又抵消了下降部分，使其变成 水平线，那么到底多少个正弦波才能形成一个矩形呢，其实是无穷多个。（上帝：我皮不皮）不仅仅是矩形，任何波形都可以由无数个正弦波聚合到一起。

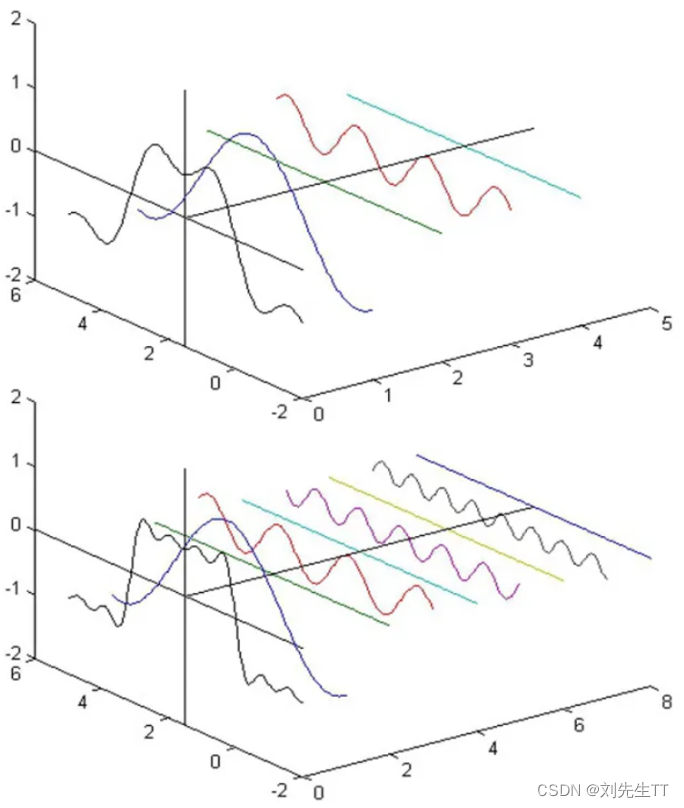
我们可以发现，最前面的黑线是由几个正弦波组成的，越来越多正弦波拟合出来的形状与时域中的长方形越像，效果越好，而两条正弦波中的值线，代表不具有该频率的一个正弦波，为了特殊的正弦波图像，有些频率的正弦波是不需要的。
让我们看看老师是怎末解视正弦波的，他就是圆周运动在一条直线上的投影。使用欧拉公式可以进行表示。后面将相信介绍。

观察下面的动图，我们发现不同的圆周运动组合到一起（也就是不同的正弦波）会产生不同的图形。

用另一种方式来表示正弦波，就是下图这种方式，大家最开始看可能会想，这是什么东西。

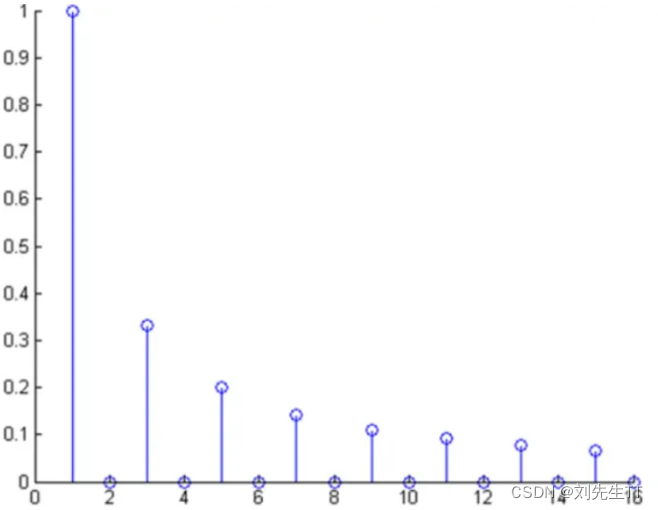
补上下面这长度大家就可以理解了，不过就是换了个方向观察，从正面看它相当于在时域进行观察，从侧面看相当于在频域进行观察，进一步通俗的理解，时域和频域的不同无非就是一个函数在不同维度下的情况。

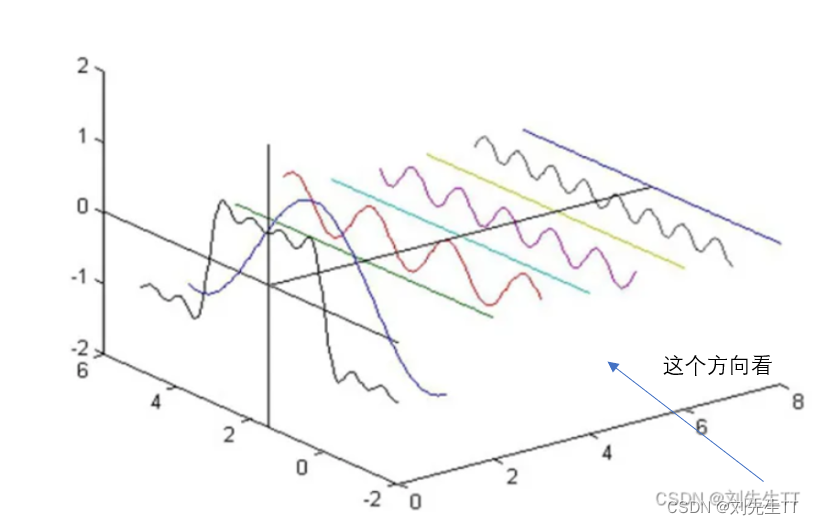
下面这个图大家是不是更直白了些。

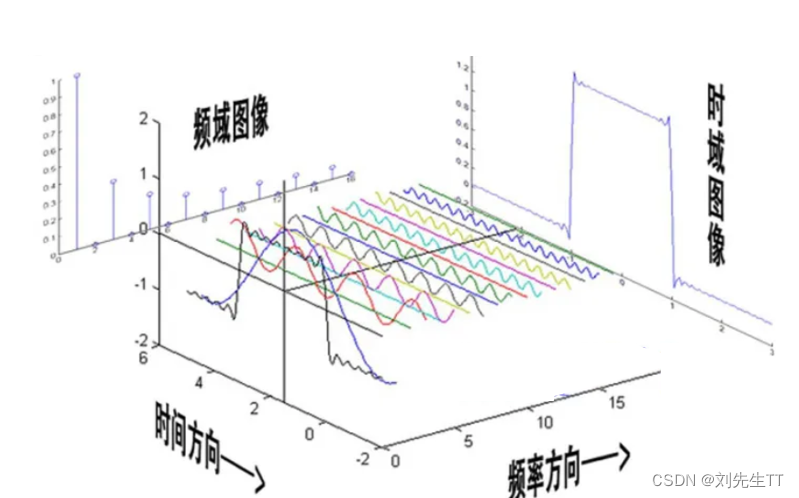
傅里叶级数的相位谱

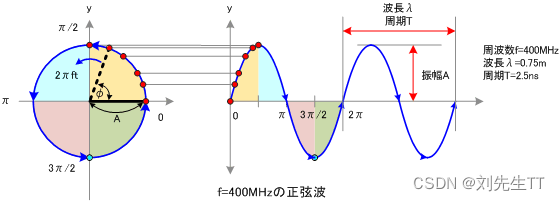
从正面看是时域空间的图像，侧面看是频域空间的图像，那么从下面看呢，没错与主题有关，就是相位谱。相位大家可能都有了解，就是一个正弦波平移的度量，

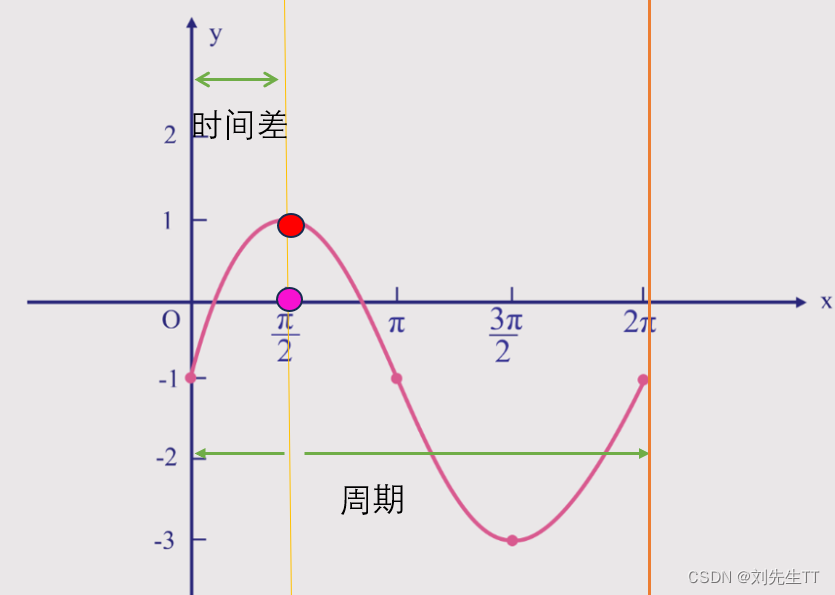
鉴于正弦波是周期的，我们需要设定一个用来标记正弦波位置的东西。在图中就是那些小红点。小红点是距离频率轴最近的波峰，而这个波峰所处的位置离频率轴有多远呢？为了看的更清楚，我们将红色的点投影到下平面，投影点我们用粉色点来表示。当然，这些粉色的点只标注了波峰距离频率轴的距离，并不是相位。
这里需要纠正一个概念：时间差并不是相位差。如果将全部周期看作2Pi或者360度的话，相位差则是时间差在一个周期中所占的比例。我们将时间差除周期再乘2Pi，就得到了相位差。
补充上图，来一个大集合，方便大家对时域、频域、相位谱有一个充分的了解。

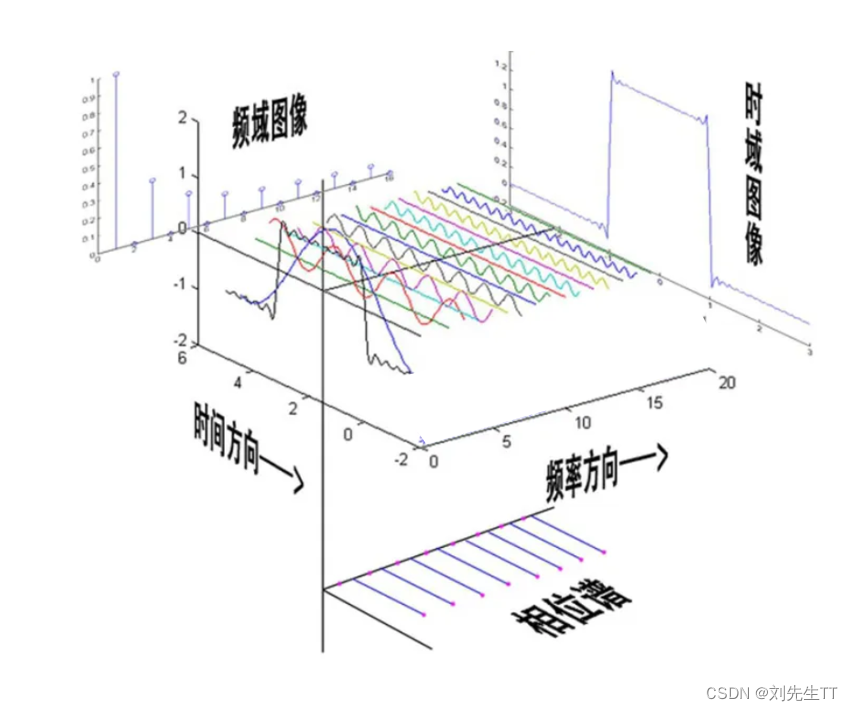
傅里叶变换

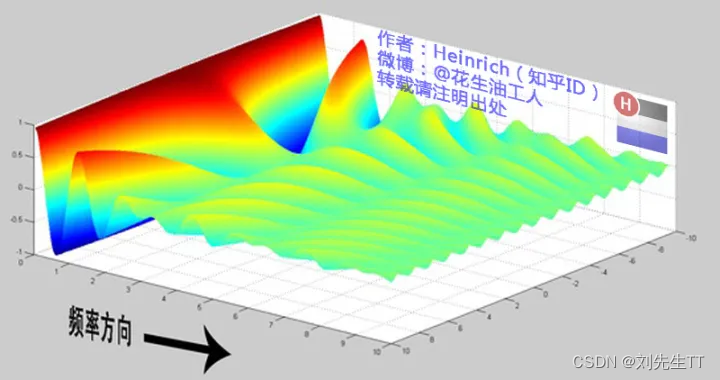
傅里叶变换是将时域中的函数转换为频域中的函数，其中频域我们发现其是由不同频率的正弦波组成，横坐标为频率、纵坐标为振幅，而将不同的正弦波连续起来，大家可以想像海浪的形状。

傅里叶公式如下所示
$$F(w)={\int }_{-\infty }^{+\infty }f(x)e^{-iwx}dx$$
大家第一次看见这个公式肯定会很懵这是什么东西？下面我一步一步进行分析。

欧拉公式

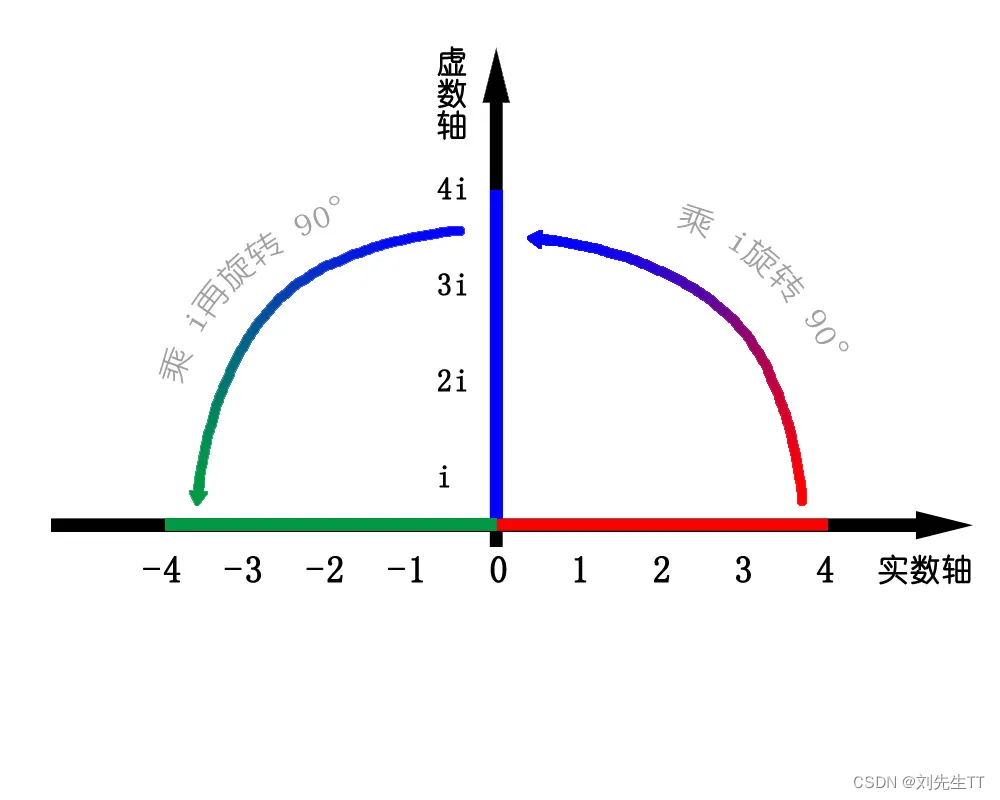
高中的时候，相信大家都学习国复数，其中的i表示-1的平方根。我们将4乘上-1就是在实数轴上转一百八十度，而-1=i乘i。 那么如果我们将4乘上i呢?没错，就是旋转90度

e^t次方图像如下所示。

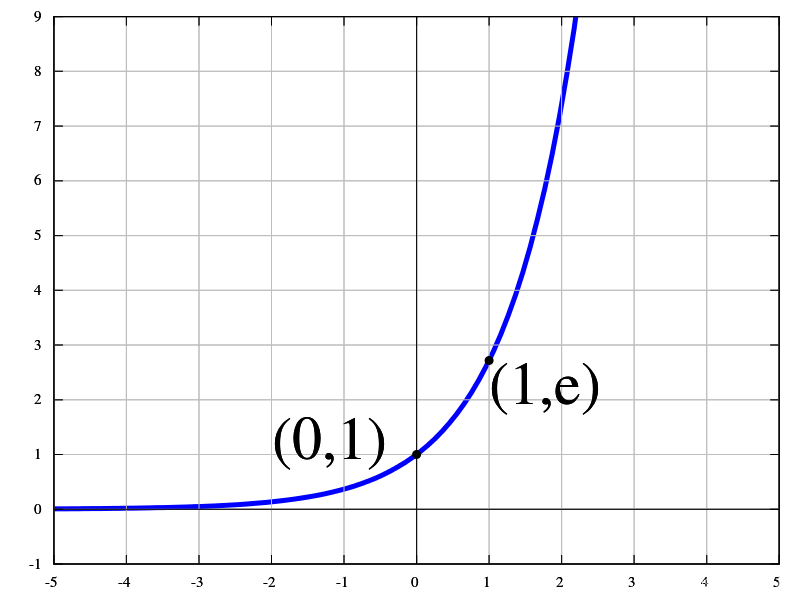
但是我们将二者结合，将t加上i之后呢，那么我们变会得到如下的图像。

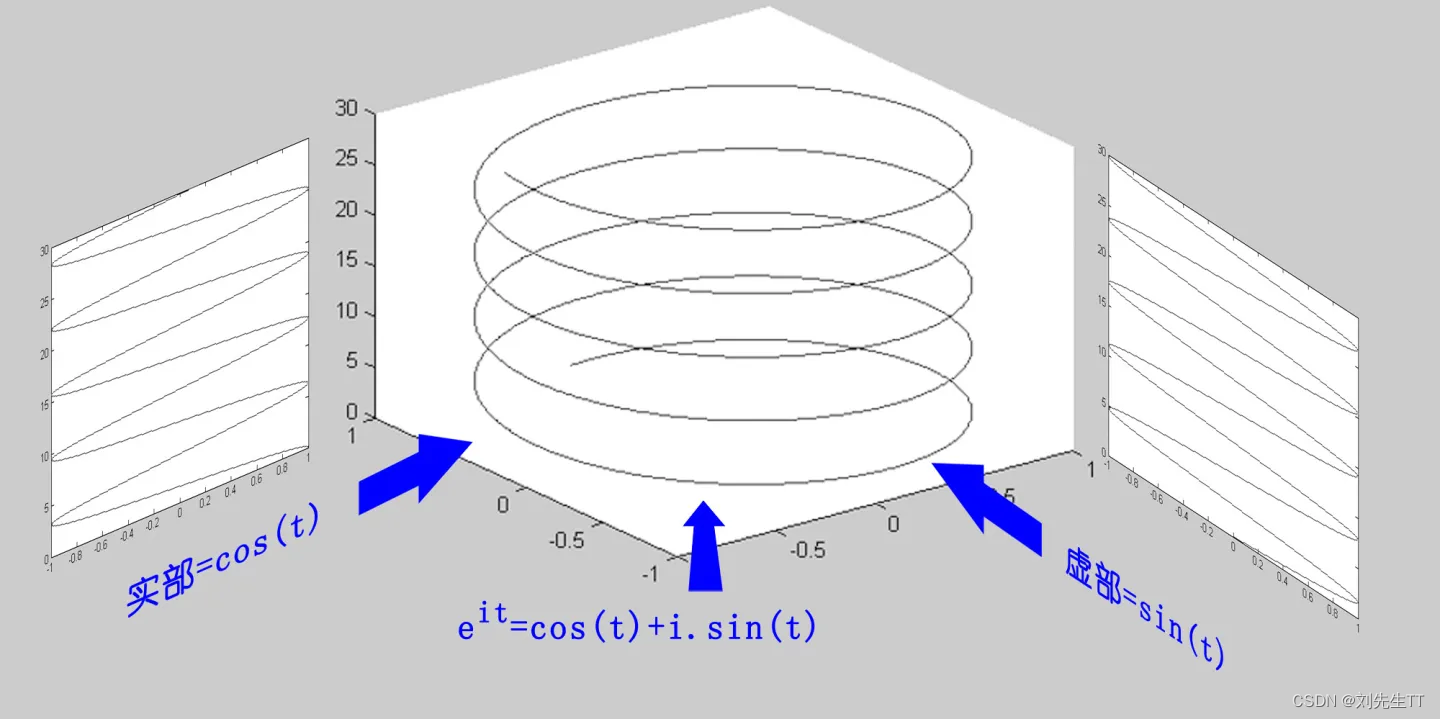
没错，将实数域的图像扩展到了复数域。其实部为cos(t)虚部为sin(t)。因此我们可以理解欧拉公式了。
$$e^{i\theta }=cos(\theta )+i\ast sin(\theta )$$

观察该图，我们发现横坐标正好与实部对应，纵坐标和虚部对应。
如果w我们进行如下的变换。将其中的角度用频率来表示。
$$\theta =wt$$
那么得出
$$e^{iwt}=cos(wt)+i\ast sin(wt)$$
随着t的增加表示其沿着圆圈逆时针旋转。
下面公式则表示这他向顺时针旋转$$e^{-iwt}$$
诶，是不是与傅里叶变换的后半部分对应上了，如果你忘记了请你翻翻之前的笔记，并且加深印象。

基向量和内积关系

任何一个维度的向量都可以由当前维度下的基向量线性相加表示出来。
观察下图，我们可以发现基向量为e^x ,e ^y，而我所画的向量等于 2e ^x+e ^y,可以通过基向量组合进行表示。

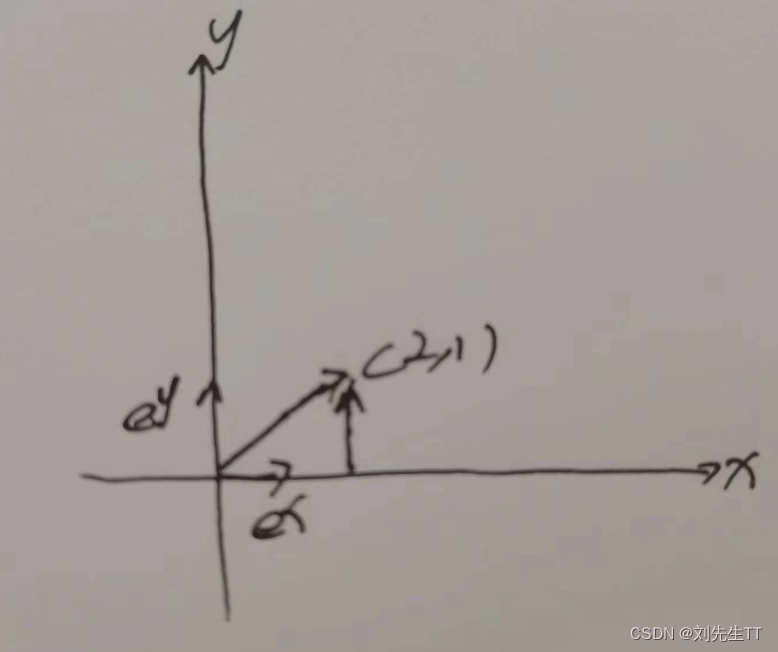
因此如果我用该向量对两个基向量做内积，他的值都不会为0，因为他们不是正交的。
得出结论：如果某一向量中含有任一基向量，那么该向量与该基向量的内积不为0。
傅里叶变换可以理解为从时域到频域的一个空间变换，因此如果原始向量与频域中的正弦波进行内积不为0的话，那么就表示该正弦波是原始向量在频域的基向量，是不是与最开始所说的对应上了，一个长方形可以有任意无限多正弦波组成。现在我们再看傅里叶变换的公式
$$F(w)={\int }_{-\infty }^{+\infty }f(x)e^{-iwx}dx$$
其中积分号里面表示做内积来进行正弦波的筛选。如果有则不为0，没有则为0，进而进行时域对频域的转换，
相信大家对傅里叶变换的公式有了更深一步的了解。

参考：

B站首发！草履虫都能看懂的【傅里叶变换】讲解
复数的意义