（四）航空发动机强度与振动复习纲要

第6章 圆盘振动

6.1 圆盘振动现象

轮盘的结构型式可分为中心轴联结（中心固定）的轮盘和外缘联结（边缘固定）的轮盘。

▶轮盘的振动形式可以分为：第一类振动：（节圆振动），这类振动一般不会导致轮盘的损坏；第二类振动：（节径振动），这类振动容易引起轮盘的损坏；复合振动。

（1）第一类振动—————振动形式中心对称，即全部节线都是同心圆。中心固定的一阶振动又称伞形振动。
对于外缘固定的圆盘，振动时没有中心节点，节圆情况类似。
节圆振动不严重，一般不会导致盘的损坏。

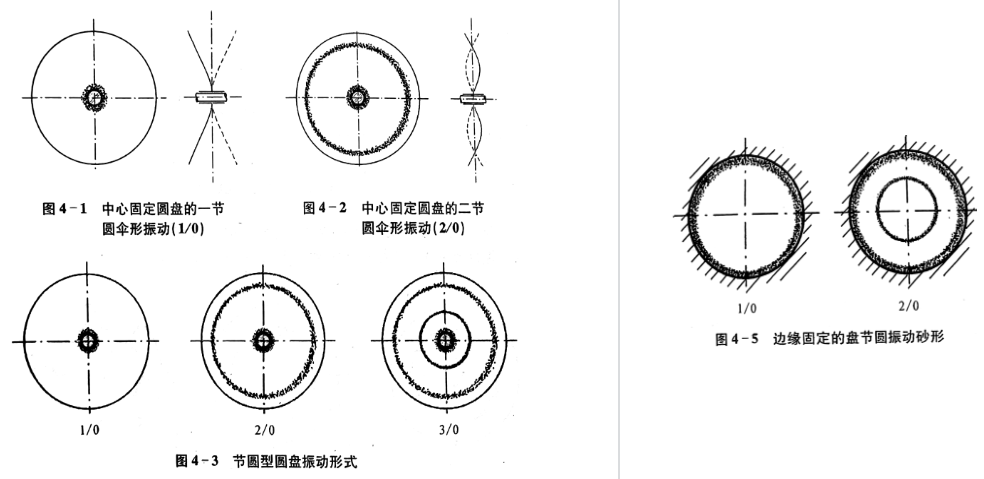
（2）第二类振动————全部节线都是沿圆盘面均匀分布的直径，称为节径。
这类振动无论在中心固定或边缘固装的圆盘都可能产生。这类振动最容易引起轮盘的损坏。

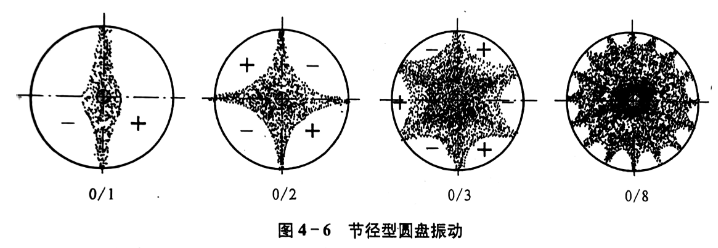
（3）复合振动

将各类振动编以标记符号。其中分子为节圆数，分母为节径数。

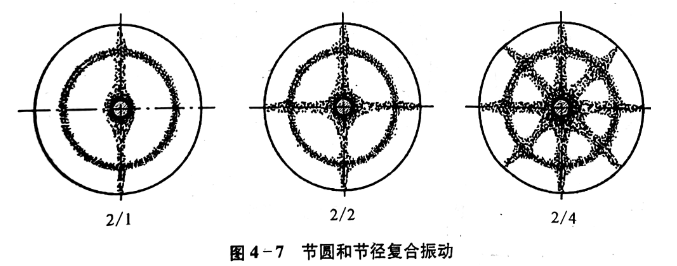
☛[选择题]判断下面轮盘的振动类型（C）

A、弯曲振动 B、节圆振动 C、节径振动 D、伞形振动

6.2 等厚圆盘的自振频率

圆盘的各种自振频率随其转速增加而增加。

高温使轮盘处理的弹性模量减小，从而导致轮盘的振动固有频率下降。

6.3 动波

第二类振动在实际发动机中最常见，下面详细分析这类振动。
与叶片振动类似，在求解盘的节径振动问题中，采用极坐标，写出振幅方程如下：
$$W=W_0\left(r,\theta \right)\cos pt$$
$W_0$表示圆盘各位置的振幅，具体写为：
$$W_0\left(r,\theta \right)=U\left(r\right)\cos \theta$$
$U(r)$表示在一定半径$r$的圆周上的最大振幅。

对于$m$个节径的振动，则写为：
$$W_0\left(r,\theta \right)=U\left(r\right)\cos m\theta$$
因此，振幅方程可以写为：
$$W=U\left(r\right)\cos m\theta \cos pt=\frac{U}{2}\left[\cos \left(m\theta +pt\right)+\cos \left(m\theta -pt\right)\right]$$
上式$\frac{U}{2}\cos \left(m\theta +pt\right)$和$\frac{U}{2}\cos \left(m\theta -pt\right)$都被称为动波。

当位移为$0$时，$\cos \left(m\theta \pm pt\right)=0$，解得节线相对于盘的运动方程为：
$$\theta =\frac{i\pi }{2m}\pm \frac{p}{m}t$$
得到对应的角速度：$\frac{d\theta }{dt}=\pm \frac{p}{m}$

因此“动波”有下列特性：
①全圆周上任何时间都有$2m$个节点、极大值和极小值；
②这些节点（与其他点一起）随时间以一定角速度$\pm \frac{p}{m}$在圆周上旋转；
③两个动波具有相同的角频率和幅值，但旋转方向相反。

当盘以$\omega$的速度旋转时，如果动波移动方向与$\omega$相同，称为顺动波；反之称为逆动波。

逆动波相对于地面的角速度${\omega }_2$为：${\omega }_2=\frac{p_d}{m}-\omega$（$p_d$是旋转情况下盘的自振频率，比静止盘要高）
可以看出，当$p_d=m\omega$时，${\omega }_2=0$，于是得出如下结论：

▶（逆动波）的移动速度和盘的旋转速度相等，波形将在空间停止不动，称为（驻波）。

6.4 盘振动的激振力

引起盘振动的激振力大致有三种来源：

（1）叶片受到周期性变化的气体力传递给盘；
（2）其它零件的力通过联接环或轴传递给盘；
（3）盘面气体压力不均，或有周期性变化。

第7章 发动机的振动与平衡

7.1 临界转速

▶轴的挠度达到最大值时，这时轴的转速就称为（临界转速）。

平衡转子

假设一个弯曲平衡的轴盘系统，盘的重心与轴线重合，忽略轴的质量，并忽略盘重产生的静挠度。会有两种情况：
（1）不管什么转速下，盘的重心始终在旋转轴线上，轴不发生任何挠度。

（2）旋转时，轴发生挠度，只有在特定转速（临界转速）下，盘的离心力与轴的弹性恢复力平衡，此时轴可以产生任何挠度。

盘的离心力为：$my{\omega }^2$ 轴的弹性恢复力为：$Cy$（$C$为刚性系数）

列出平衡方程：$my{\omega }^2=Cy$ ，解得临界转速为：${\omega }_{cr}=\sqrt{\frac{C}{m}}$

综述：完全平衡的轴－盘系统除非在特定转速下，轴可以产生任何挠度外，其它情况下，轴都不会有挠度。（✔）

不平衡转子

假设盘的重心与旋转轴不重合，带有一定的偏心距$e$，盘装在跨度中央，此时无陀螺力矩。轴旋转时会有两种情况：

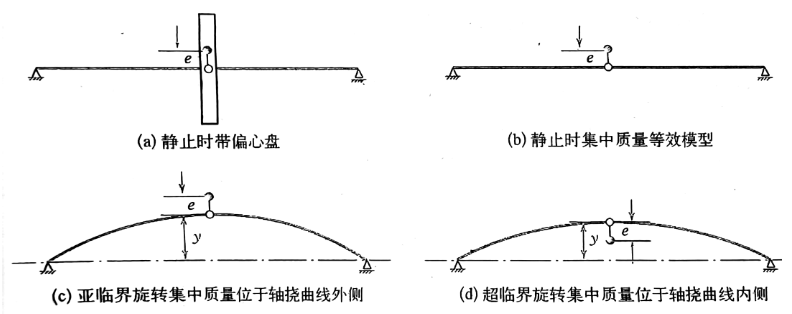
（一）亚临界状态

平衡方程为：
$$m{\omega }^2\left(y+e\right)=Cy$$
解得挠度$y$为:
$$y=\frac{e}{\frac{C}{m{\omega }^2}-1}=\frac{e}{{\left(\frac{p}{\omega }\right)}^2-1}=\frac{{\left(\frac{\omega }{p}\right)}^{2}e}{1-{\left(\frac{\omega }{p}\right)}^2}=\frac{{\left(\frac{\omega }{{\omega }_{cr}}\right)}^{2}e}{1-{\left(\frac{\omega }{{\omega }_{cr}}\right)}^2}$$
此时$\omega <{\omega }_{cr}$，轮盘质心位于轴挠曲线的外侧。

（二）超临界状态

平衡方程为：
$$m{\omega }^2\left(y-e\right)=Cy$$
解得挠度$y$为:
$$y=\frac{e}{1-\frac{C}{m{\omega }^2}}=\frac{e}{1-{\left(\frac{p}{\omega }\right)}^2}=\frac{{\left(\frac{\omega }{p}\right)}^{2}e}{{\left(\frac{\omega }{p}\right)}^2-1}=\frac{{\left(\frac{\omega }{{\omega }_{cr}}\right)}^{2}e}{{\left(\frac{\omega }{{\omega }_{cr}}\right)}^2-1}$$
此时$\omega >{\omega }_{cr}$，轮盘质心位于轴挠曲线的内侧。

总结：

①在$\omega =p=\sqrt{\frac{C}{m}}$时，挠度$y$将无限增大，远离此处，挠度明显减小。偏心距存在与否，并不影响临界转速；
②对于同一转子，平衡得越好，$e$值越小，同一转速下，挠度呈比例下降，良好的平衡能减少振动；
③图中左右两支曲线并不对称，左支代表亚临界状态，右支代表超临界状态；
④当转子由亚临界越过临界过渡到超临界时，质心将由外侧转向内侧。

▶不平衡转子旋转时，在临界转速以下，处于（亚临界）状态；在临界转速以上，处于（超临界）状态。

偏心距的存在与否不影响转子临界转速的数值，因此，对转子的平衡并不能减少振动。（✘）

不完全平衡的轴-盘系统除非在特定的转速下，轴才有挠度。（✘）

当转子由亚临界越过临界而过渡到超临界时，质心将由挠曲线内侧转向外侧。（✘）

✈[例1]有单盘实心轴转子，尺寸如下图所示。设盘的偏心距为$3\times 10^{-5}\mathrm{m}$，求$n=2000$和$3000\mathrm{rpm}$时，轴在装盘处的挠度。假设无摩擦和陀螺力矩。

由题目可知：$E=2.1\times 10^{11}\mathrm{Pa}$，$J=\pi d^4/64=3.976\times 10^{-8}{\mathrm{m}}^4$，$m=5\mathrm{kg}$，$l=1.2\mathrm{m}$，$a=0.4/1.2=1/3$；

可算出轴在装盘处的刚性系数：
$$C=\frac{3EJ}{a^2{\left(1-a\right)}^2{l}^3}=2.935\times 10^5\mathrm{N}/\mathrm{m}$$
临界转速：
$$\begin{gathered} {\omega }_{cr}=\sqrt{\frac{C}{m}}=242.3\mathrm{rad}/\mathrm{s} \\ {n}_{cr}=\frac{60{\omega }_{cr}}{2\pi }=2314\mathrm{rpm} \end{gathered}$$
当$n=2000\mathrm{rpm}$时，盘处于亚临界状态
$$\omega =\frac{2\pi n}{60}=209.4\mathrm{rad}/\mathrm{s}$$
故盘处挠度为：
$$y=\frac{e{\left(\frac{\omega }{{\omega }_{cr}}\right)}^2}{1-{\left(\frac{\omega }{{\omega }_{cr}}\right)}^2}=\frac{3\times 10^{-5}\times {\left(\frac{209.4}{242.3}\right)}^2}{1-{\left(\frac{209.4}{242.3}\right)}^2}=8.85174\times 10^{-5}\mathrm{m}$$
当$n=3000\mathrm{rpm}$时，盘处于超临界状态
$$\omega =\frac{2\pi n}{60}=314.2\mathrm{rad}/\mathrm{s}$$
故盘处挠度为：
$$y=\frac{e{\left(\frac{\omega }{{\omega }_{cr}}\right)}^2}{{\left(\frac{\omega }{{\omega }_{cr}}\right)}^2-1}=\frac{3\times 10^{-5}\times {\left(\frac{314.2}{242.3}\right)}^2}{{\left(\frac{314.2}{242.3}\right)}^2-1}=7.40184\times 10^{-5}\mathrm{m}$$

7.2 轴质量对临界转速的影响

先讨论光轴（不带盘）的临界转速，对轴上一微元段进行受力分析：

把离心力作为分布载荷，建立微分方程如下：
$$\frac{d^2}{d{x}^2}\left(EJ\frac{d^{2}y}{d{x}^2}\right)=q=m_1{\omega }^{2}y$$
$m_1$为单位长度的质量，对于等截面的均质轴，$EJ$为常数，令$a^4=\frac{m_1{\omega }^2}{EJ}$，故得：
$$\frac{d^{4}y}{d{x}^4}=a^{4}y$$
对于双简支梁，上述微分方程的特征方程为：
$$\sin al=0$$
解得$(al{)}_i=i\pi ,i=1,2,3\cdots$故得一系列的临界转速值为：
$${\omega }_{cr}=a_i^2\sqrt{\frac{EJ}{m_1}}=\frac{{\left(al\right)}_i^2}{l^2}\sqrt{\frac{EJ}{A\rho }}$$
因此前三阶转速：${\omega }_{cr,1}:{\omega }_{cr,2}:{\omega }_{cr,3}=f_{cr,1}:f_{cr,2}:f_{cr,3}=1:4:9$

现在讨论考虑轴质量的单盘转子的临界转速。设盘装在双简支轴的中央，且轴的临界转速与分布质量的光轴一样。

分布质量的光轴可以折合为中央带集中质量的$m_{折}$的无重轴，折合质量可由下式解出：
$${\omega }_{cr,1}=\sqrt{\frac{C}{m_{\text{折}}}}=\frac{{\pi }^2}{l^2}\sqrt{\frac{EJ}{A\rho }}$$
再考虑轴中央装有盘的情形:
$${\omega }_{cr,1}=\sqrt{\frac{C}{m_{\text{折}}+m_{\text{盘}}}}$$
经过变换可得顿克（Dunkerley）公式：
$$\frac{1}{{\omega }^2}=\frac{1}{{\omega }_0^2}+\frac{1}{{\omega }_1^2}$$
此处$\omega$（$={\omega }_{cr,1}$）是该系统一阶临界转速，${\omega }_0$、${\omega }_1$分别为光轴和单盘无重轴的临界转速。

注意：①只能用于一阶临界转速；②不考虑陀螺力矩；③该公式是近似的，当盘位置接近支承时，误差较大；对于悬臂转子误差更大；④计算值低于精确值。

多盘转子的临界转速

对顿克公式进行推广，可得：
$$\frac{1}{{\omega }_{cr}^2}=\frac{1}{{\omega }_0^2}+\frac{1}{{\omega }_1^2}+\frac{1}{{\omega }_2^2}+\cdots$$
其中，${\omega }_{cr}$————考虑轴质量的多盘转子的一阶临界转速；

​ ${\omega }_0$————光轴的临界转速；

​ ${\omega }_1$————无重轴，只带盘1的系统临界转速；

​ ${\omega }_2$————无重轴，只带盘2的系统临界转速；

​ …

✈[例2]已知双支点等截面带盘的轴如下图所示，分别计算下列三种情况的临界转速：（1）光轴（不计盘质量）；（2）单盘无重轴；（3）单盘计入轴质量。

已知：
$$\begin{gathered} E=2.1\times 10^{11}\mathrm{Pa} \\ \rho =7.8\times 10^3\mathrm{kg}/{\mathrm{m}}^3 \\ A=\pi d^2/4=7.069\times 10^{-4}{\mathrm{m}}^2 \\ J=\pi d^4/64=3.976\times 10^{-8}{\mathrm{m}}^4 \\ m=5\mathrm{kg} \\ l=1.2\mathrm{m} \\ a=0.4/1.2=1/3 \end{gathered}$$
（1）光轴：
$$\begin{gathered} {\omega }_{cr}^{\prime }=\frac{{\pi }^2}{l^2}\sqrt{\frac{EJ}{A\rho }}=266.7\mathrm{rad}/\mathrm{s} \\ {n}_{cr}^{\prime }=\frac{60{\omega }_{cr}^{\prime }}{2\pi }=2547\mathrm{rpm} \end{gathered}$$
（2）单盘无重轴：

轴在装盘处的刚性系数：
$$C=\frac{3EJ}{a^2{\left(1-a\right)}^2{l}^3}=2.935\times 10^5\mathrm{N}/\mathrm{m}$$
临界转速：
$$\begin{gathered} {\omega }_{cr}^{{}^{\prime \prime }}=\sqrt{\frac{C}{m}}=242.3\mathrm{rad}/\mathrm{s} \\ {n}_{cr}^{{}^{\prime \prime }}=\frac{60{\omega }_{cr}}{2\pi }=2314\mathrm{rpm} \end{gathered}$$
（3）单盘计轴质量：

根据顿克公式：
$$\begin{gathered} \frac{1}{{\omega }_{cr}^2}=\frac{1}{{\left({\omega }_{cr}^{\prime }\right)}^2}+\frac{1}{{\left({\omega }_{cr}^{{}^{\prime \prime }}\right)}^2} \\ {\omega }_{cr}=179.3\mathrm{rad}/\mathrm{s} \\ {n}_{cr}=\frac{60{\omega }_{cr}}{2\pi }=1712\mathrm{rpm} \end{gathered}$$

7.3 处理临界转速问题的方法

（1）将转子的临界转速调到发动机的最大转速以上

一般认为临界转速应高于最大工作转速的$30\%$，就可以避开大的振动。

（2）将转子的临界转速调到发动机的最低转速以下

（3）增加阻尼器或挠度阻尼器

▶对轴的挠度起到抑制效果最常用而有效的是（挤压油膜）阻尼器
（4）利用非线性的作用

（5）改善转子的平衡

7.4 发动机转子的平衡

▶发动机转子不平衡的表现形式有：（静不平衡）和（动不平衡）两种。

转子外径D与其长度L满足D/L<5时，不论其工作转速高低都只需进行静平衡。（✘）[D/L>5,需静平衡]