Markov模型|马尔科夫家族、MDP建模+PYTHON实现

已于 2023-12-21 18:38:42 修改
阅读量1.6k 收藏 30
点赞数 16
文章标签： 机器学习 人工智能 深度学习 python 数据挖掘 算法
于 2023-12-21 18:28:11 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_52373687/article/details/135137265
版权

 

 1.Markov模型

  • 1.1基本介绍

        Markov是一个庞大的家族，是有马尔可夫性质（Markov property）的一类概率模型。其中，在马尔可夫过程中，我们考虑一个状态空间，该空间中的每个状态都与一个特定的概率相关。马尔可夫性质指出，在一个随机过程中，在给定当前状态的条件下，未来状态的条件分布只依赖于当前状态，而与过去的状态无关。换句话说，它具有“无记忆”或“无后效性”的特性。这意味着，在马尔可夫过程中，我们可以仅基于当前状态来预测未来的状态。

        而且，马尔可夫链（Markov Chain）是描述离散时间马尔可夫过程的一种常见形式。它由一系列状态和在状态之间转移的概率组成。每个状态之间的转移概率称为转移概率矩阵。通过使用转移概率矩阵，我们可以计算在给定初始状态的情况下，随着时间的推移，系统处于不同状态的概率。

        另一个与马尔可夫相关的概念是隐马尔可夫模型（Hidden Markov Model，HMM）。HMM是一种常见的统计模型，用于建模具有隐含状态的观测数据序列。在 HMM 中，状态是不可观察的，而我们只能观测到与状态相关的输出。通过学习和推断，我们可以根据观测序列来估计隐藏状态的序列

        马尔可夫决策过程（Markov Decision Process，MDP）中，马尔可夫链的概念被引入到决策问题中。MDP是一种建模具有状态、动作和奖励的决策问题的工具。在MDP中，每个状态都有一个关联的奖励，智能体根据当前状态和可选的动作来选择决策，目标是最大化累积奖励。通过使用值函数、策略等概念，我们可以根据MDP模型来求解最优的决策策略，这在强化学习等领域中有广泛的应用。

        马尔科夫链蒙特卡洛（Markov Chain Monte Carlo，MCMC）是一种用于模拟复杂概率分布的统计方法。MCMC是一种基于马尔科夫链的采样方法，在采样过程中利用随机漫步来探索样本空间。通过在马尔科夫链中迭代生成样本，并且样本按照一定的概率保持在某些状态上，最终得到的样本集合可以用来估计概率分布的性质，如均值、方差等。

        马尔科夫随机场（Markov Random Field，MRF）是一种用于建模随机变量之间的相互依赖关系的概率图模型。它由一组随机变量组成的图结构表示，其中每个节点表示一个随机变量，边表示变量之间的依赖关系。MRF 通过定义一组能量函数来描述变量之间的关系，这些能量函数通常基于变量的局部邻域。

        部分可观测马尔科夫决策过程（Partially Observable Markov Decision Process，PDMDP）是对 Markov Decision Process（马尔科夫决策过程）的扩展，其中决策者在每个状态下观察到的信息是不完全的。决策者在每个状态下接收到的观测结果取决于当前状态以及隐藏的环境状态。因此，决策者需要根据这些观测结果来选择最优的行动策略。

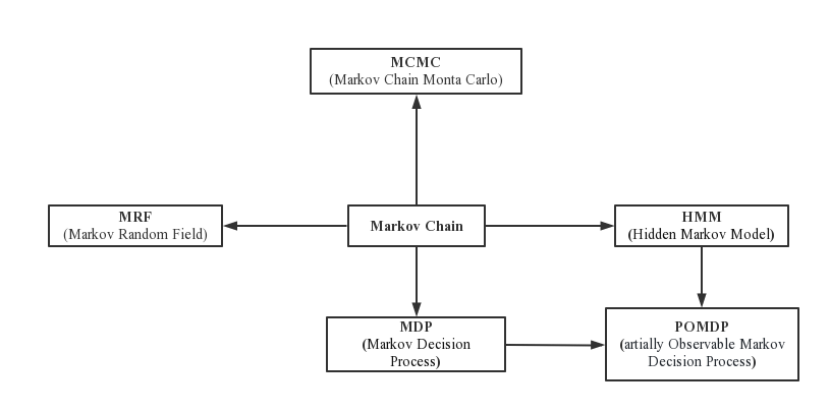
图 1 Markov家族图

1.2基本概念

1.2.1马氏链概念

马尔可夫链中的基本概念如下：

  • 状态（State）：马尔可夫链中每个可能的情况或状态称为一个状态。例如，在天气预测中，状态可以是"晴天"、"雨天"或"多云"等。
  • 转移概率（Transition Probability）：定义了从一个状态到另一个状态的转移概率。对于任意两个状态 i 和 j，转移概率 P(i, j) 表示在当前状态为 i 的条件下，下一个状态为 j 的概率。

  • 转移图（Transition Diagram）：用图形方式表示马尔可夫链的状态和状态之间的转移关系。每个状态作为一个节点，转移概率则表示为边。
  • 初始分布（Initial Distribution）：马尔可夫链开始时的状态分布概率，表示在初始时刻各个状态的概率分布。
  • 马尔可夫性（Markov Property）：即未来状态的概率只与当前状态有关，与过去的状态无关。这意味着给定当前状态，以及当前状态之前的所有历史状态，未来状态的概率分布只由当前状态决定。

1.2.2马氏链举例

在这里我们举一个小例子来更清晰阐述这马尔可夫链：

假设有一名学生，他的日常生活有三种状态：学习、休息和出去玩，并且他明天的状态只基于或取决于他今天的状态。这三种状态我们定义具体的转移规则，如下：

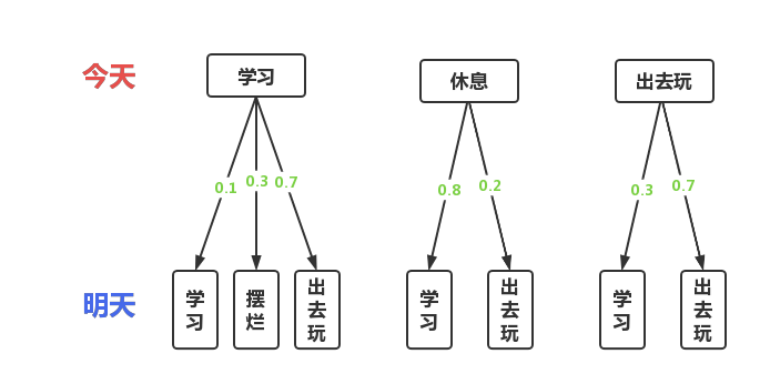
图 2 状态转移规则图示

由此我们可以画出状态转换图：

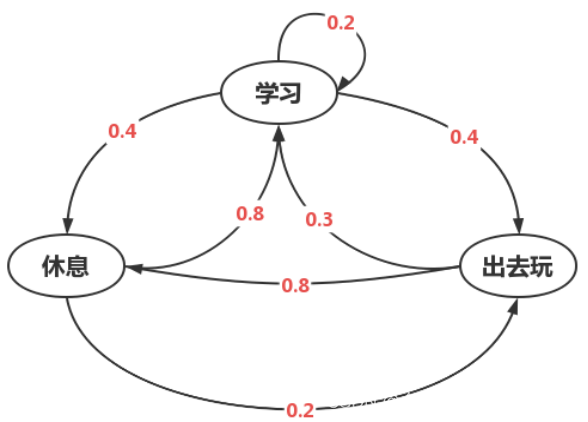
图 3 状态转移图

状态的转移矩阵P为：

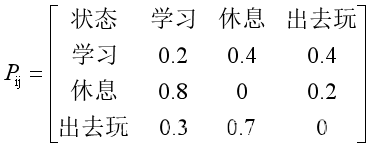
然后我们还定义初始状态的概率为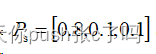：。在这个模型下，我们可以求解各种概率：

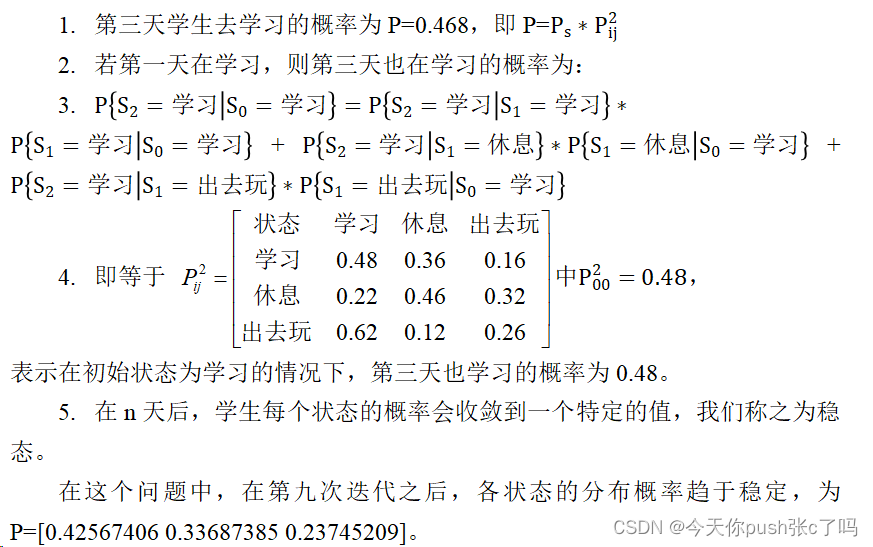
1.2.3MDP基本概念

        MDP是马尔科夫链的扩展，增加了决策者在每个状态下做出的决策的概念。MDP 用于描述决策问题，其中决策者根据当前状态和可能的行动选择，以最大化长期累积奖励。故跟马尔可夫链相比，MDP的概念有如下特点：

  1. 决策者和行动：在 MDP 中，除了状态转移概率，还引入了决策者的行动选择。决策者在每个状态下可以选择多个行动中的一个，并且行动的选择会影响状态的转移。与马尔可夫链不同，MDP 强调决策者在每个状态下面临的决策问题。
  2. 奖励函数：MDP 引入了奖励函数，用来评估决策者在每个状态下所获得的即时奖励。决策者的目标是通过选择行动来最大化长期累积的奖励。马尔可夫链没有考虑具体的奖励函数。
  3. 目标和策略：MDP 规定了一个目标，通常是最大化累积奖励，以及一个策略，即一组决策者在每个状态下采取行动的规则。马尔可夫链没有明确的目标和策略的概念。

图 4 MDP过程图示

1.2.4 MDP求解算法

        求解马尔可夫决策过程（MDP）模型的算法有多种，每种算法都有其独特的优缺点和适用范围：

1. 值迭代算法

        优点：收敛速度快、易于编程实现、可用于在线计算

        缺点：算法执行时间复杂度高，不适用于具有大量状态空间的问题

        适用范围：适用于状态空间较小的 MDP 模型求解，能够较好地解决具有确定转移的离散问题。

2. 策略迭代算法

        优点：相较于值迭代算法收敛速度较快、可用于非确定性模型的求解并且一定程度上更稳定

        缺点：需要对策略进行评估操作，因此迭代次数较多，时间复杂度也相对高。

        适用范围：适用于具有确定转移的离散问题的 MDP 模型求解，特别适用于解决非确定性问题。

3. Q-learning算法

        优点：能够解决连续空间问题，行动空间大的 MDP 模型求解，也能到达对抗环境下的解决问题。

        缺点：可能无法收敛，在某些情况下会产生过度估计和向一侧偏移的问题。

        适用范围：适用于连续空间问题，行动空间大的 MDP 模型求解，另外还可以用于在强化学习无法采用监督学习的情况下的最优策略求解问题。

4. SARSA算法

        优点：能够解决连续空间问题，行动空间大的 MDP 模型求解，具有广泛的应用范围。

        缺点：需要事先建立模型，算法可能不够有效能。

        适用范围：适用于连续空间问题，行动空间大的 MDP 模型求解，在模型已知的情况下，也是一种常用的 Q-learning 算法的替代方案。

5. DQN算法

        优点：相较于 Q-learning 算法可以使用神经网络解决高维状态空间问题，并且法适用于大规模数据上训练。

        缺点：不稳定性高，容易出现过拟合问题。

        适用范围：适用于高维状态空间问题求解，可以使用神经网络进行优化和求解。

6. PPO算法

        优点：采用了重要性采样技术，允许在更新策略时使用历史轨迹的样本数据，提高了样本利用率;使用了一种优化约束，确保策略变化不过大，从而保证训练的稳定性和收敛性;相对简单易实现，同时具有较好的性能；在训练过程中可以动态调整优化步长，并具有自适应性

        缺点：需要大量的样本集进行训练，可能需要更多的时间和计算资源。

        适用范围：适用于于连续动作空间的强化学习问题。

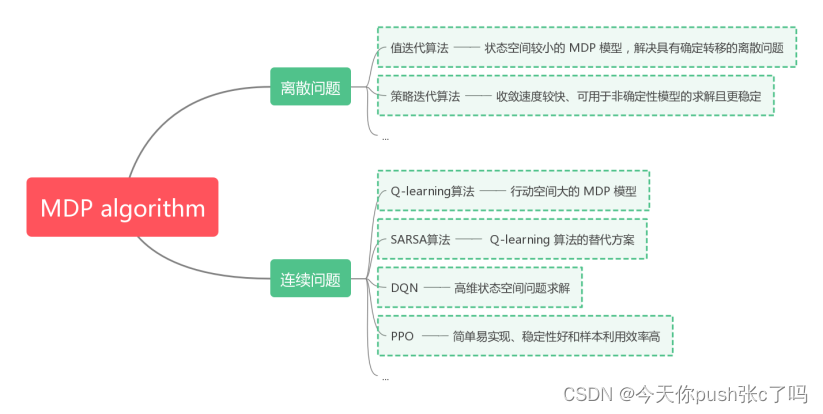
图 5 MDP算法

  • 2. Markov模型在管理学的应用

  • 2.1 应用概述

        马尔可夫模型在管理学中具有广泛的应用，特别是在运筹学、供应链管理、金融风险管理和市场营销等领域。下面将介绍Markov模型在这些领域的具体应用。

  • 库存管理

        马尔可夫模型可以用于预测和优化库存水平。通过分析过去的需求和出货模式，模型可以识别不同库存状态之间的转移概率，从而进行库存水平的优化和预测。有研究针对血小板的库存控制问题，考虑短缺、浪费和输血新鲜度之间的平衡，以效用最大化为目标建立有限时域的马尔科夫决策过程模型，探讨最优的血小板订货策略和使用策略(李猜等, 2019)。

  • 客户行为分析

        马尔可夫模型可以分析客户行为模式，了解不同转移状态下客户的购买行为、偏好和行为模式。然后，这些分析结果可以用于制定精确的市场推广策略和客户关系管理。在客户CRM的研究当中，有学者提出了一种针对银行业客户行为预测的马尔可夫链模型，利用客户状态变量RF构建相应的客户转移矩阵(李纯青等, 2011)。

  • 供应链和项目管理

        在供应链中，马尔可夫模型可以用于预测供应链节点之间的转移和需求模式。这有助于优化物流计划、预测库存需求以及保持供应链的高效运转；在项目管理中，马尔可夫模型可以帮助预测不同项目阶段之间的状态转移。通过分析过去的项目数据，可以预测项目完成的时间、资源需求以及可能的风险。

  • 维修和保养计划

        在设备维修和保养方面，马尔可夫模型可以用于提前预测设备故障和维护需求。通过分析不同设备状态之间的转移概率，模型可以帮助制定更有效的维修和保养计划，以减少停机时间和维修成本。

        在下一部分具体例子详述中，该研究就在考虑系统可靠性和维护费用的情况下，将优化问题描述为具有离散和连续混合状态和行动空间的无限水平MDP，以最大化总折扣回报为目标。通过设计一个参数化的动作空间结构和多任务强化学习框架，解决了混合动作空间带来的困难(Zhang等, 2023)。

2.2 论文具体应用详述

        在该部分，我们运用论文中的具体实例来系统展示MDP的建模过程。

        在系统可靠性相关研究中，考虑到现有研究缺少对维修过程的动态过程和关于负载分担的研究，有学者提出了一种求解暂态OM优化问题的无限水平MDP框架。在保证系统性能的前提下，以期望维护费用最小为目标，根据各部件的节点健康状况和负载状态动态选择维护动作。为准备DRL算法，设计了参数化的动作空间。下面主要介绍状态空间、动作空间、状态转移函数和优化公式。

  1. 定义状态空间：

  • 确定行动集合：定义系统可以采取的行动集合，每个状态下的行动可以是离散的或连续的。

在每个检查时间步长，有四个互不相容的维护操作，包括什么都不做、纠正更换、PM和OM。每个组件必须从四个动作中选择一个，以在每个时间步长执行。这四种操作中有离散和连续两种类型，为了将他们效率结合起来一起表示，设计了如下图所示的参数空间，量化他们的效率。PM和OM的维护效率在[0，1]的范围内被参数化.

图 6 维修动作参数化

故步骤k处的动作空间被定义为：

  • 设立状态转移模型：

  • 确定即时奖励函数：对定义在每个状态和采取每个行动后系统所获得的即时奖励（可负可正）。该模型的目标是在可接受的维护预算下保持稳定的运行性能。故MDP的目标是最大化期望的贴现回报，综合可靠系统获得的利润和在时间范围内的维护成本。奖励函数

是给定在时间步长k的状态和动作的即时奖励。对于上面所表达的MDP，奖励是完成生产任务所获得的利润减去第k次检查中的维护动作所产生的维护成本。利润的大小取决于多态系统的绩效水平。即时奖励函数表示如下：

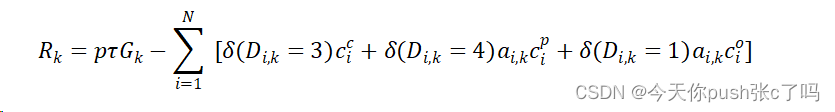
  • 确定目标函数：

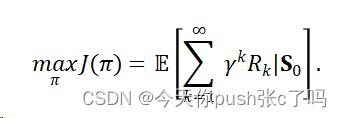
  • 开始策略迭代或值迭代：

  • 评估和优化策略：使用得到的最优策略或值函数进行模拟或实际测试，评估系统的性能并进行优化。根据评估结果，可以调整模型参数或策略，以满足特定需求或优化目标。该论文中运用了两个例子来进行实际测试。两个说明性示例中表示，定制的DRL方法可以有效地识别具有可接受的运行时间的最优OM策略。

  • 3. 基本软件使用

  • 3.1软件概述

马尔可夫模型可以使用多种软件工具进行建模和分析。以下是一些常用的软件工具：

R：R是一种广泛使用的统计分析软件，具有丰富的统计和机器学习功能。在R中，可以使用各种包（如"markovchain"和"HMM"）来建立和分析马尔可夫模型。

Python：Python是一种通用编程语言，也被广泛用于数据科学和机器学习。在Python中，可以使用库（如"numpy"和"scipy"）进行马尔可夫模型的建模和分析。

MATLAB：MATLAB是一种专业的数值计算和科学编程环境，也可用于马尔可夫模型的建模。MATLAB提供了丰富的统计和机器学习工具箱，例如"Statistics and Machine Learning Toolbox"。

SAS：SAS是一种流行的商业分析软件，也支持马尔可夫模型的建模。SAS提供了广泛的统计分析和数据挖掘功能，可以用于创建和分析马尔可夫模型。

HMMToolbox：HMMToolbox是一个专门用于隐马尔可夫模型的开源软件工具包。它提供了各种算法和函数来构建和分析隐马尔可夫模型。

3.2MDP建模示例

3.2.1问题描述

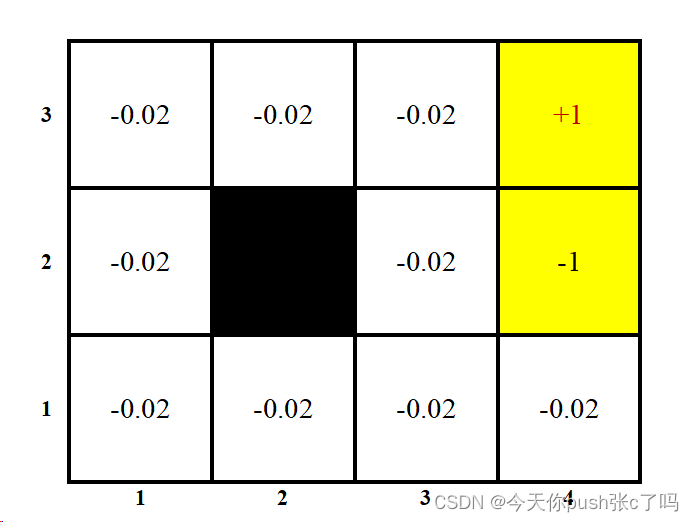
3.2.2求解步骤

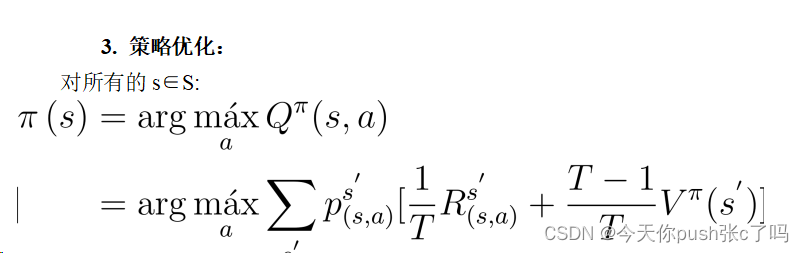
3.2.3 代码实现

import numpy as np
###part1:输入MDP四元组<S, A, P, R>, 累积奖赏参数T
S=[(1,1),(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4)];
size_state=len(S);#状态向量
final_state=[(2,4), (3,4)]
A=['n', 'e', 'w', 's'];size_action=len(A);#actions向量
P=[];#转移概率矩阵
for i in range(size_state):
    if S[i] in final_state:
        action_state=[{i:1},{i:1},{i:1},{i:1}]
    else:
        action_state=[]
        for j in range(size_action):
            state=S[i]; action=A[j];
            if action=='n':
                state_pro={i:0}
                next_state=(state[0]+1, state[1])
                if next_state in S:
                    state_pro[S.index(next_state)]=0.8;
                else:
                    state_pro[i]=state_pro[i]+0.8;
                next_state=(state[0], state[1]+1);
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1;
                next_state=(state[0], state[1]-1)
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1
                action_state.append(state_pro)
            elif action=='e':
                state_pro={i:0}
                next_state=(state[0], state[1]+1)
                if next_state in S:
                    state_pro[S.index(next_state)]=0.8;
                else:
                    state_pro[i]=state_pro[i]+0.8;
                next_state=(state[0]+1, state[1]);
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1;
                next_state=(state[0]-1, state[1])
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1
                action_state.append(state_pro)
            elif action=='w':
                state_pro={i:0}
                next_state=(state[0], state[1]-1)
                if next_state in S:
                    state_pro[S.index(next_state)]=0.8;
                else:
                    state_pro[i]=state_pro[i]+0.8;
                next_state=(state[0]+1, state[1]);
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1;
                next_state=(state[0]-1, state[1])
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1
                action_state.append(state_pro)
            else:
                state_pro={i:0}
                next_state=(state[0]-1, state[1])
                if next_state in S:
                    state_pro[S.index(next_state)]=0.8;
                else:
                    state_pro[i]=state_pro[i]+0.8;
                next_state=(state[0], state[1]+1);
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1;
                next_state=(state[0], state[1]-1)
                if next_state in S:
                    state_pro[S.index(next_state)]=0.1;
                else:
                    state_pro[i]=state_pro[i]+0.1
                action_state.append(state_pro)
    P.append(action_state)
    R = np.array([-0.02, -0.02, -0.02, -0.02, -0.02, -0.02, -0.23, -0.02, -0.02, -0.02, 1]);  # rewards
print(P)
T=100;#累积步长
###part2:初始化
value=np.zeros(size_state); #初始化value
policy=np.zeros((size_state, size_action))+1/size_action;# 初始化policy
###part3:策略估计
T_MAX=100;
for t in range(1,T_MAX+1):
    value_new=np.zeros(size_state);
    for state in range(size_state):#对所有s,计算对应的value
        for action in range(size_action):#对某个s,按照当前策略选取a
            state_action_state=P[state][action]
            q_state_action=0
            for next_state in state_action_state:#(s, a)下，转移到s'的概率
                trans_pro=state_action_state[next_state]
                q_state_action=q_state_action+trans_pro*(R[next_state]/t+value[next_state]*(t-1)/t);
            value_new[state]=value_new[state]+policy[state][action]*q_state_action
    if t==T+1:
        break
    else:
        value=value_new[:]
print(value);
###part3:选取最优策略
new_policy=[0 for i in range(size_state)];
opt_policy=[0 for i in range(size_state)];
policy_stable=True
while policy_stable:
    for state in range(size_state):#对所有s,求对应的最优策略a
        q_state_actions=[]
        for action in range(size_action):#对某个s,对所有可能采取的a计算Q(s, a)
            state_action_state=P[state][action]
            q_state_action=0
            for next_state in state_action_state:
                trans_pro=state_action_state[next_state]
                q_state_action=q_state_action+trans_pro*(R[next_state]/T+value[next_state]*(T-1)/T);
            q_state_actions.append(q_state_action)

        new_policy[state]=q_state_actions.index(max(q_state_actions));
    if new_policy==opt_policy:
        policy_stable=False
    else:
        opt_policy=new_policy

###输出结果
print('opt_policy:', opt_policy)

参考文献：

[1]李猜, 耿娜, & 王春鸣. (2019). 基于MDP的血小板库存最优订货策略和使用策略研究. 运筹与管理, 28(7), 108–117. C类. [2]李纯青, 袁亮, & 马军平. (2011). 马尔可夫链概率矩阵的银行业客户行为预测. 西安工业大学学报, 31(06), 554–558. https://doi.org/10.16185/j.jxatu.edu.cn.2011.06.004 [2]Zhang, C., Li, Y.-F., & Coit, D. W. (2023). Deep Reinforcement Learning for Dynamic Opportunistic Maintenance of Multi-Component Systems With Load Sharing. IEEE Transactions on Reliability, 72(3), 863–877. Q1. https://doi.org/10.1109/TR.2022.3197322

今天你push了吗
关注
  • 16
    点赞
  • 踩
  • 30
    收藏
    觉得还不错? 一键收藏
  • 0
    评论
动态规划：求解MDP的经典方法
禅与计算机程序设计艺术
05-14 827
1. 背景介绍 1.1 马尔可夫决策过程（MDP）概述 马尔可夫决策过程（Markov Decision Process, MDP）是一种用于建模顺序决策问题的数学框架，其中主体（agent）根据当前状态选择行动，以最大化长期累积奖励。MDP的核心思想
MDP的决策迭代和值迭代
星云
03-24 2607
MDP（马尔可夫决策过程） 给定当前状态ts^t\boldsymbol sts，未来t+1s^{t+1}\boldsymbol st+1s和过去t−1s^{t-1}\boldsymbol st−1s是独立的。对于MDP，行动ta^{t}\boldsymbol ata的结果t+1s^{t+1}\boldsymbol st+1s仅取决于当前状态ts^t\boldsymbol sts，而和过去没关系，这种特性有时被称为“无记忆性”。 这个过程可以概括为五个部分： S\mathcal SS：状态集，S=
Gauss-Markov高斯马尔可夫回归模型（Python完整源码和数据）
07-22
研究当违反五个高斯马尔可夫假设之一时对普通最小二乘回归模型的影响（Python完整源码和数据） 研究当违反五个高斯马尔可夫假设之一时对普通最小二乘回归模型的影响（Python完整源码和数据） 研究当违反五个高斯马尔可夫假设之一时对普通最小二乘回归模型的影响（Python完整源码和数据）
MarkovNetwork:Markov网络用于神经计算的Python实现
05-12
马尔可夫网络 用于神经计算的Markov网络的Python实现。 执照 请参阅以获取datacleaner的许可和使用信息。 通常，我们已为MarkovNetwork软件包授予许可，以使其尽可能广泛地使用。 安装 MarkovNetwork旨在使用NumPy数组进行快速数组处理。 因此，我们建议在安装MarkovNetwork之前先安装版。 但是，MarkovNetwork应该可以在任何基本的Python安装中正常工作。 一旦安装了先决条件，就可以使用简单的pip命令安装datacleaner： pip install MarkovNetwork 用法 创建MarkovNetwork的实例时，可以传递以下参数： num_input_states: int (required) The number of input states in the Markov Network
数学建模系列-预测模型（四）马尔可夫预测
vcvvcvx的博客
02-10 1万+
马尔可夫（Markov)预测法，就是一种关于事件发生的概率预测方法。它是根据事件的目前状况来预测其将来各个时刻（或时期)变动状况的一种预测方法。马尔可夫预测法是地理预测研究中重要的预测方法之一。1. 状态指某一件事在某个时刻（或时期）出现的某种结果。2.状态转移过程事件的发展，，称为状态转移。3.马尔可夫过程在事件的发展过程中，若每次状态的转移都仅与前一时刻的状态有关，而与过去的状态无关，或者说，则这样的状态转移过程就称为马尔可夫过程。4.状态转移概率。
二、Markov 决策过程 (MDP)
晓野豬
09-14 4941
马尔科夫决策过程 (MDP) MDP 是强化学习问题在数学上的理想化形式； MDP 是序列决策的经典形式化表达，其动作不仅影响当前的即时收益，还影响后续的状态以及未来的收益； 情节性任务（Episodic Tasks），所有的任务可以被可以分解成一系列情节，可以看作为有限步骤的任务； 连续任务（Continuing Tasks），所有的任务不能分解，可以看作为无限步骤任务； 马尔可夫性：当一个随机过程在给定现在状态及所有过去状态情况下，其未来状态的条件概率分布仅依赖于当前状态； 马尔
强化学习学习笔记（二）：Markov决策过程
weixin_46721170的博客
10-13 1139
一、Markov决策过程模型 Markov决策过程是强化学习最经典、最重要的数学模型。大多数的强化学习问题都建模成Markov决策过程。 1.离散时间Markov决策过程 1.1数学表示 智能体观察状态的环境，得到观测,其中是状态空间，表示状态取值的综合;是观测空间，表示观测取值的综合。智能体根据观测决定做出动作，其中是动作合集。环境根据智能体的动作，给予智能体奖励,并进入下一步状态，其中是奖励空间，表示奖励取值的集合，它是实数集R的...
（2-2）马尔可夫决策过程（MDP）：MDP的组成要素
最新发布
码农三叔
02-08 1558
在马尔可夫决策过程（MDP）中，状态空间（State Space）是一个定义了问题中所有可能状态的集合。状态（State）用来描述系统或环境的特定情况或配置。状态空间的定义对于建立问题的形式化模型非常重要，它需要清晰地包含所有可能的状态，以便智能体能够在其中进行决策。状态通常可以是离散的或连续的，具体取决于问题的性质。（1）状态空间（State Space）状态空间是一个集合，通常用符号S表示。它包含了问题中所有可能的状态。状态空间可以是有限的，也可以是无限的。（2）状态（State）
【大道至简】机器学习算法之隐马尔科夫模型(Hidden Markov Model, HMM)详解（2）---计算问题：前向算法和后向算法原理详解公式推导及Python实现
尚拙的博客
12-17 2876
对于后向算法的理解，从定义出发非常重要。我看网上包括很多教学视频，对这部分内容的讲解几乎是一笔带过，基本上都是说：和前向算法类似，只不过这边是反过来计算而已，这里不再多说了，大家自己看书。我觉得这么说是很不负责任的，因为对于大多数数学天赋没那么好的人真的仔细理解后向算法，还是需要花点时间的，如果没有人指点，可能真的就需要费很大劲（我就是）。为了让大伙不再走太多弯路，我接下来尽最大可能把自己已经搞明白的知识给大家分享。
强化学习算法-基于python的sarsa算法实现
06-02
在Python实现SARSA时，首先需要定义环境，这通常是一个简单的MDP（Markov Decision Process，马尔科夫决策过程）。环境可以是像Gridworld这样的模拟环境，也可以是更复杂的游戏或控制系统。然后，我们需要创建一个Q...
PyPI 官网下载 | MDP-3.4.tar.gz
01-13
MDP（Markov Decision Processes）是一个用于处理动态决策问题的Python库，它为解决马尔科夫决策过程提供了工具和算法。在机器学习和强化学习领域，MDP是建模和解决问题的重要框架。PyPI（Python Package Index）是...
mdp（马尔可夫决策过程）2009年matlab源码，非常详细全面，非常实用
04-23
2009年写的matlab mdp源码，里面有全部的英文document介绍说明
隐马尔可夫模型工具 hmmer 2.3
08-31
目前可以使用的最好的hmm软件，用于模式识别
QuickPOMDPs.jl：简洁友好的界面，用于定义与POMDPs.jl一起使用的MDP和POMDP模型
02-04
马尔科夫决策过程（MDP）是一种数学模型，用于描述具有离散时间步骤的动态环境中的决策问题，其中未来状态只依赖于当前状态和采取的行动，不考虑过去的历史。MDP 被广泛应用于强化学习、机器人控制、资源管理等领域...
ee365:python中的ee365
05-18
在Python中，可以使用库如gym、rllab或stable-baselines来实现MDP的建模和求解。 在"ee365-master"这个压缩包中，很可能包含了课程的源代码、练习题、讲义和其他教学材料。这些材料可能涵盖了以下知识点： 1. **...
pymdptoolbox.zip
02-18
马尔科夫决策过程（Markov Decision Process，简称MDP）是一种用于建模具有不确定性的动态决策问题的数学框架，广泛应用于强化学习、人工智能、运筹学和控制理论等领域。在Python中，处理MDP的库相对较少，而`...
机器学习——马尔可夫模型及马尔可夫决策过程（MDP）
热门推荐
zhongyoubing的博客
11-07 2万+
一、马尔可夫模型1. 马尔可夫链设表示随机变量X在离散时间t时刻的取值。若该变量随时间变化的转移概率仅依赖于它的当前值，即：也就是时候状态转移概率指依赖于前一个状态，称这个变量为马尔可夫变量，其中 为随机变量X可能的状态，这个性质称为马尔可夫性质，具有马尔可夫性质的随机过程称为马尔可夫过程。马尔可夫链是满足马尔可夫性质的随机过程，指在一段时间内随机变量X的取值序列（）满足上述性质2、转移概率马尔可夫
如果环境存在random，那么问题还能建模成MDP吗？
mmc2015的专栏
03-16 566
李宏毅老师的课程：https://www.youtube.com/watch?v=W8XF3ME8G2I老师说，对于同一个observation/state（atari game的画面），也不一定会采取相同的动作，因为有些actor是stochastic的，选action有一定随机性，这一点好理解。。。老师还说，即便actor采取同一个action，得到的reward和next state也不一定...
python RTL自动生成_玩点好玩的Python：使用马尔可夫模型自动生成文章
weixin_39789206的博客
11-22 73
前言你会因为写文章而苦恼吗？想不想利用Python的马尔可夫模型帮助你自动生成文章，接下来看代码吧首先导入库import nltkimport random主体代码file = open('Text/Walden.txt', 'r')walden = file.read()walden = walden.split()def makePairs(arr): pairs = [] for i in ...
使用灰色预测模型和马尔科夫模型进行预测的Python代码的具体实例
05-24
以下是一个使用灰色预测模型和马尔科夫模型进行预测的Python代码示例： ``` import numpy as np from sklearn.metrics import mean_squared_error # 灰色预测模型 def GM11(x0): # 累加生成序列 x1 = np.cumsum(x0) z1 = (x1[:-1] + x1[1:]) / 2.0 # 紧邻均值平滑处理 z1 = z1.reshape((len(z1), 1)) B = np.append(-z1, np.ones_like(z1), axis=1) Y = x0[1:].reshape((len(x0) - 1, 1)) # 计算参数 [[a], [b]] = np.dot(np.dot(np.linalg.inv(np.dot(B.T, B)), B.T), Y) # 建立灰色预测模型 model = lambda k: (x0[0] - b / a) * np.exp(-a * (k - 1)) - (x0[0] - b / a) * np.exp(-a * (k - 2)) # 预测结果 predict = np.array([model(i) for i in range(1, len(x0) + 5)]) return predict # 马尔科夫模型 def markov_predict(data, n_steps=5, split_ratio=0.8): # 数据切分 train_size = int(len(data) * split_ratio) train_data = data[:train_size] test_data = data[train_size:] # 建立状态转移矩阵 states = sorted(list(set(train_data))) n_states = len(states) state_idx = {states[i]: i for i in range(n_states)} trans_matrix = np.zeros((n_states, n_states)) for i in range(len(train_data) - 1): cur_state = state_idx[train_data[i]] next_state = state_idx[train_data[i + 1]] trans_matrix[cur_state][next_state] += 1 for i in range(n_states): row_sum = sum(trans_matrix[i]) if row_sum > 0: trans_matrix[i] /= row_sum # 预测 last_state = state_idx[train_data[-1]] predict_probs = np.dot(np.linalg.matrix_power(trans_matrix, n_steps), trans_matrix[last_state]) predict = states[np.argmax(predict_probs)] return predict # 示例数据 data = np.array([120, 130, 135, 140, 145, 150, 155, 160, 165, 170]) # 灰色预测 gm_predict = GM11(data) # 马尔科夫模型预测 markov_predicts = [] for i in range(len(data) - 1): markov_predicts.append(markov_predict(data[:i+1])) markov_rmse = np.sqrt(mean_squared_error(data[1:], markov_predicts)) print('马尔科夫模型RMSE:', markov_rmse) # 输出结果 print('原始数据：', data) print('灰色预测结果：', gm_predict) print('马尔科夫模型预测结果：', markov_predicts) ``` 上述代码中，使用了`GM11`函数实现了灰色预测模型，该函数接受一个原始数据序列作为输入，并输出预测结果序列。使用`markov_predict`函数实现了马尔科夫模型，该函数接受一个原始数据序列、预测步数和数据切分比例作为输入，并输出预测结果。在示例中，分别对原始数据进行了灰色预测和马尔科夫模型预测，并输出了预测结果。

“相关推荐”对你有帮助么？

  • 非常没帮助
  • 没帮助
  • 一般
  • 有帮助
  • 非常有帮助
提交
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值