一、多项式及其函数
(一)多项式的表达式和创建
M
A
T
L
A
B
MATLAB
MATLAB中使用一维向量来表示多项式,将多项式的系数按照降幂次序存在在向量中,其具体表示方法如下:
P
(
x
)
=
a
0
x
n
+
a
1
x
n
−
1
+
.
.
.
+
a
n
−
1
x
+
a
n
⇒
[
a
0
,
a
1
,
.
.
.
,
a
n
−
1
,
a
n
]
P(x)=a_0x^{n}+a_1x^{n-1}+...+a_{n-1}x+a_n \Rightarrow [a_0,a_1,...,a_{n-1},a_n]
P(x)=a0xn+a1xn−1+...+an−1x+an⇒[a0,a1,...,an−1,an]
例如,多项式
2
x
4
+
3
x
3
+
5
x
2
+
1
2x^4+3x^3+5x^2+1
2x4+3x3+5x2+1就可以用向量
[
2
,
3
,
5
,
0
,
1
]
[2,3,5,0,1]
[2,3,5,0,1]
对于系数为0的项依然要在向量中出现
function s = pprintf(p)
%pprintf 该函数可将一维向量转变为字符串格式的数学表达式 % p:输入参数,格式为一维向量 % s:输出参数,格式为字符串
if nargin>1 %输入参数过多时的判断
error('Too much input arguements');
end
while(p(1)==0) %输入向量的元素全为0
p(1)=[];
end
L=length(p); %计算向量长度
s='';
for v=1:L
if p(v)==0 %当常数项为0
continue;
elseif L==1 %当向量长度为1
s=strcat(num2str(p(v)));
elseif v==L %当v为向量最后一个值
s=strcat(s,'+',num2str(p(v)));
elseif v==1 %当v为向量第一个值
s=strcat(num2str(p(v)),'x^{',num2str(L-v),'}');
elseif p(v)==1 %当向量元素的值为1
s=strcat(s,'+','x^{',num2str(L-v),'}');
else
s=strcat(s,'+',num2str(p(v)),'x^{',num2str(L-v),'}');
end
end
end

(二)多项式求根(roots())、由根创建多项式(poly())
1.特定函数roots可以求解一个多项式的根
返回结果为解的向量
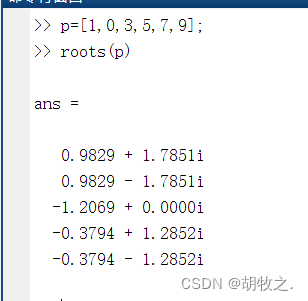
2.使用函数poly由根构造相应的多项式

(三)多项式的四则运算
1.多项式加法
当阶次相同时,多项式相加与数组相加的规则一致;
当阶次不同时,要先对低阶多项式补零,再进行相加
function p = ppadd(a,b)
% 实现阶次不同的多项式相加
if nargin<2
error('Not enough input arguments')
end
a=a(:).';
b=b(:).';
na=length(a);
nb=length(b);
p=[zeros(1,nb-na),a]+[zeros(1,na-nb),b];

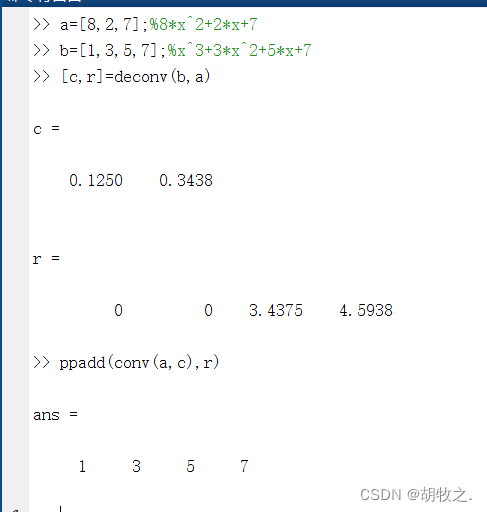
2.多项式乘法
MATLAB中,函数conv支持多项式乘法(运算法则为两个数组的卷积)

3.多项式除法
MATLAB中,函数deconv支持多项式除法(使用长除法进行解卷积,同时返回商和余数)
[c,r]=deconv(b,a) c为商,r为余数,此时满足 b==conv(a,c)+r
(四)多项式的导数polyder、积分polyint、计算函数值polyval
1.多项式的导数
MATLAB中,函数polyder可以用于多项式求导

2.多项式的积分
MATLAB中,函数polyint可以用于多项式积分,其具体句法格式如下:
polyint(P,k) 返回多项式P的积分,积分常数项为k,k默认值为0

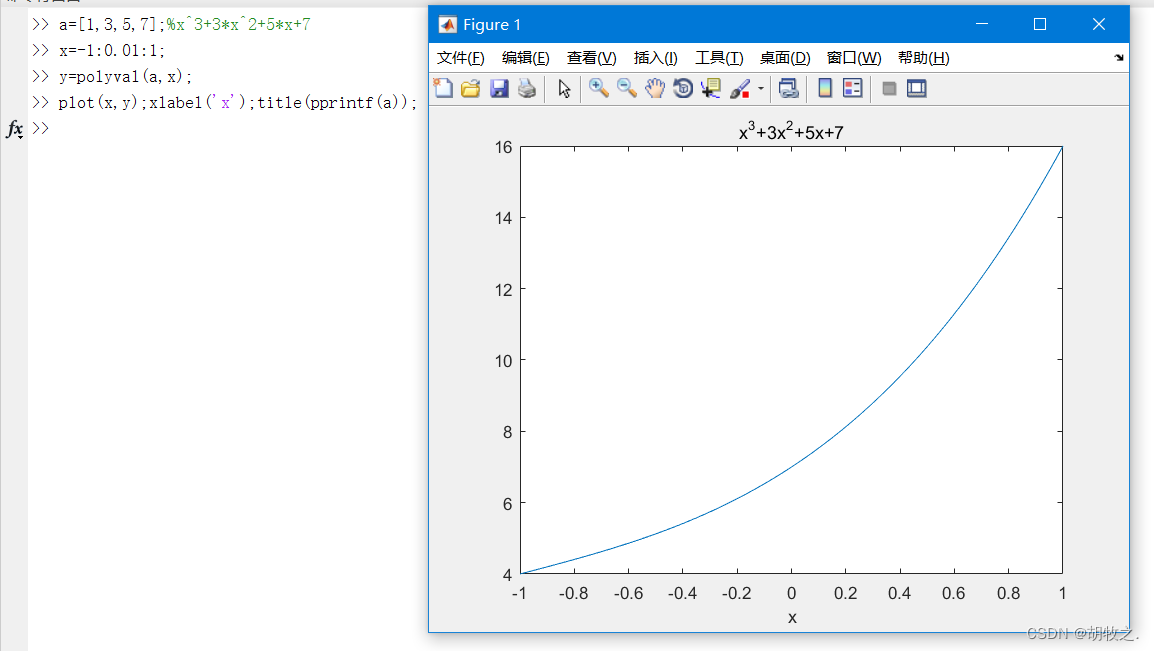
3.多项式求函数值
MATLAB中,函数polyval可以用于多项式计算函数值
(五)多项式运算函数及操作指令
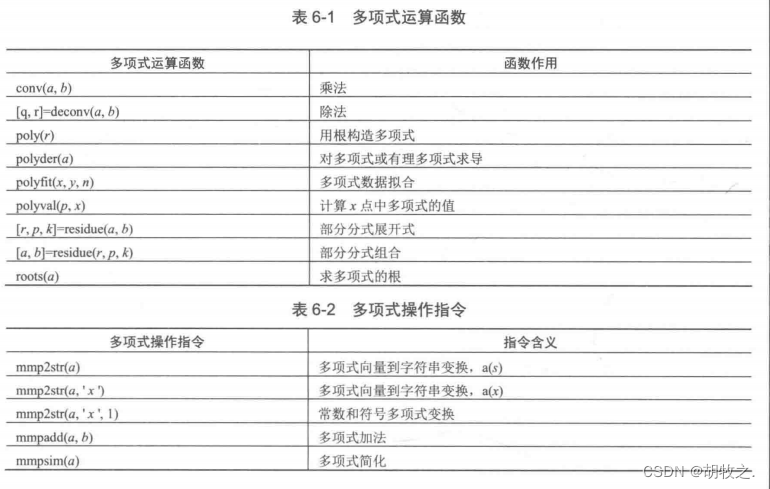
以上多项式操作函数在MATLAB中不存在已有函数可以实现
之前已经介绍了pprintf(向量到字符串变换)、ppadd(多项式加法)
再补充一下psim(多项式简化)
function y = psim(x,tol )
% psim删除多项式中近似为零的第一个系数
if nargin<2,tol=norm(x)*1000*eps;end
x=x(:).';%保证输入是行向量
i=find(abs(x)<.99&abs(x)<tol);
x(i)=zeros(1,length(i));
i=find(x~=0);
if isempty(i)
y=0;
else
y=x(i(1):length(x));
end

(六)有理多项式(部分分式展开,求导)
在许多应用中,例如傅里叶
(
F
o
u
r
i
e
r
)
(Fourier)
(Fourier)、拉普拉斯
(
L
a
p
l
a
c
e
)
(Laplace)
(Laplace)和
Z
Z
Z变换中,出现了两个多项式之比
在
M
A
T
L
A
B
MATLAB
MATLAB中,有理多项式由它们的分子多项式和分母多项式表示
b
(
x
)
a
(
x
)
=
b
0
x
m
+
b
1
x
m
−
1
+
.
.
.
+
b
m
−
1
x
+
b
m
a
0
x
n
+
a
1
x
n
−
1
+
.
.
.
+
a
n
−
1
x
+
a
n
\frac{b(x)}{a(x)}=\frac{b_0x^{m}+b_1x^{m-1}+...+b_{m-1}x+b_m}{a_0x^{n}+a_1x^{n-1}+...+a_{n-1}x+a_n}
a(x)b(x)=a0xn+a1xn−1+...+an−1x+anb0xm+b1xm−1+...+bm−1x+bm
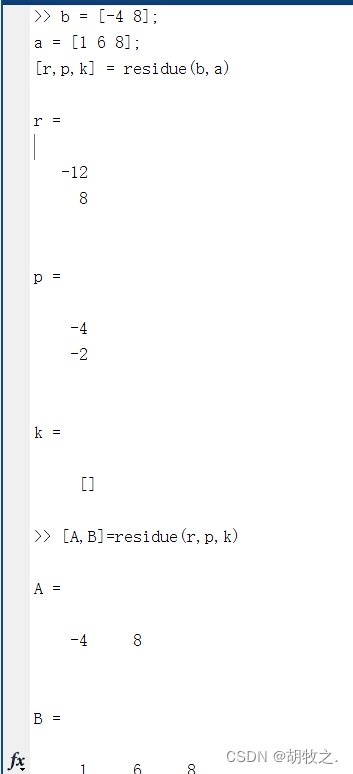
1.多项式的展开 residue函数
[r,p,k]=residue(b,a)
函数residue返回两个多项式之比的部分分式展开的留数r、极点p和直接项k
[b,a]=residue(r,p,k)
逆过程,得到分子多项式和分母多项式
2.有理多项式的求导

二、数据插值(近似表达式预测插值点)
(一)概述:插值问题
插值问题,其数学定义如下:
由实验或测量的方法得到函数
y
=
f
(
x
)
y=f(x)
y=f(x)在互异点
x
0
,
x
1
,
.
.
.
,
x
n
x_0,x_1,...,x_n
x0,x1,...,xn处的数值
y
0
,
y
1
,
.
.
.
,
y
n
y_0,y_1,...,y_n
y0,y1,...,yn,然后构造一个函数
φ
(
x
)
\varphi(x)
φ(x)作为
y
=
f
(
x
)
y=f(x)
y=f(x)的近似表达式,即
y
=
f
(
x
)
≈
φ
(
x
)
y=f(x) \approx \varphi(x)
y=f(x)≈φ(x),使得
φ
(
x
0
)
=
y
0
,
φ
(
x
1
)
=
y
1
,
.
.
.
,
φ
(
x
n
)
=
y
n
\varphi(x_{0})=y_{0},\varphi(x_{1})=y_{1},...,\varphi(x_{n})=y_{n}
φ(x0)=y0,φ(x1)=y1,...,φ(xn)=yn
这类问题叫作插值问题, y = f ( x ) y=f(x) y=f(x)称为被插函数, φ ( x ) \varphi(x) φ(x)称为插值函数, x 0 , x 1 , . . . , x n x_0,x_1,...,x_n x0,x1,...,xn称为插值节点
插值的任务就是由已知的观测点为物理量建立一个简单的、连续的解析模型,以便能根据该模型推测该物理量在非观测点的特性
(二)一维插值 interp1()
当被插值函数y=f(x)为一元函数时,为一维插值,MATLAB中使用interp1函数实现一维插值,其调用格式如下:
Vq=interp1(X,V,Xq,METHOD) X为自变量的范围;V为函数值,或者V为长度与X一致的向量;Xq为插值点向量或数组;METHOD为字符串变量,用来设定插值方法
MATLAB提供以下几种插值方法:
MATHOD='nearst' 最邻近插值,插值点函数值估计为与该插值点最近的数据点函数值
至少提供2个点,速度最快,但平滑性最差
MATHOD='linear' 线性插值,根据相邻数据点的线性函数估计落在该区域内插值数据点的函数值
默认方法,至少提供2个点,结果连续,但顶点斜率会改变
MATHOD='spline' 三次样本插值,在相邻数据点间建立三次多项式函数,根据多项式函数确定插值数据点的函数值
至少提供4个点,速度最慢,平滑性最好,但如果输入数据不一致或数据点过近,就可能出现很差的插值结果
MATHOD='pchip'或'cubic' 立方插值,通过分段立方Hermite插值方法计算插值结果
至少提供4个点,若
MATHOD='v5cubic' 用MATLAB5版本中断三次样本插值,cubic将在未来的版本中取代v5cubic
点必须均匀间隔
选择一种插值方法,需要考虑运算时间、占用内存大小和插值的光滑程度
运算时间与占用内存的比较:
n
e
a
r
e
s
t
≈
n
e
x
t
≈
p
r
e
v
i
o
u
s
<
l
i
n
e
r
<
p
c
h
i
p
(
c
u
b
i
c
)
<
s
p
l
i
n
e
nearest \approx next \approx previous < liner < pchip(cubic) < spline
nearest≈next≈previous<liner<pchip(cubic)<spline
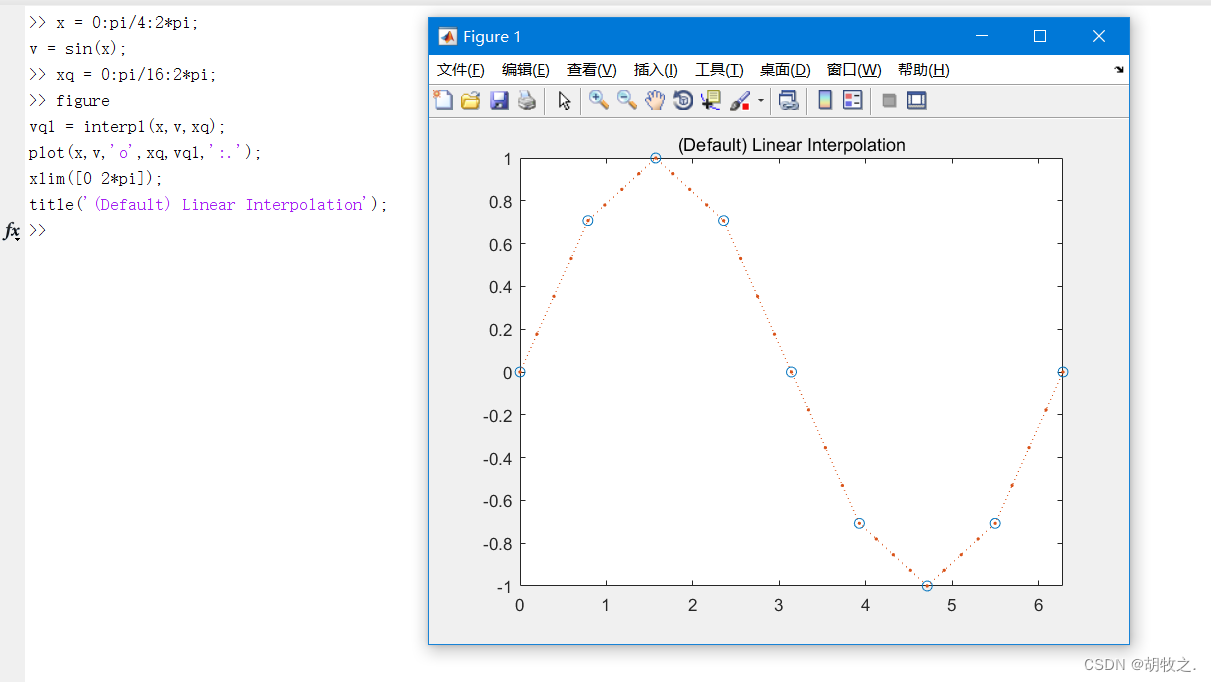
1.分段线性插值 (liner)默认方法
分段线性插值的算法是在每个小区间
[
x
i
,
x
i
+
1
]
[x_i,x_{i+1}]
[xi,xi+1]上采用简单的线性插值,在区间
[
x
i
,
x
i
+
1
]
[x_i,x_{i+1}]
[xi,xi+1]上的子插值多项式为:
F
i
=
x
−
x
i
+
1
x
i
−
x
i
+
1
f
(
x
i
)
+
x
−
x
i
x
i
+
1
−
x
i
f
(
x
i
+
1
)
F_i=\frac{x-x_{i+1}}{x_i-x_{i+1}}f(x_i)+\frac{x-x_{i}}{x_{i+1}-x_{i}}f(x_{i+1})
Fi=xi−xi+1x−xi+1f(xi)+xi+1−xix−xif(xi+1)
在此整个区间
[
x
i
,
x
n
]
[x_i,x_n]
[xi,xn]上的插值函数为:
F
(
x
)
=
∑
i
=
1
n
F
i
l
i
(
x
)
F(x)=\sum_{i=1}^{n}F_{i}l_{i}(x)
F(x)=∑i=1nFili(x)
其中
l
i
(
x
)
l_i(x)
li(x)的定义如下:
l
i
(
x
)
=
{
x
−
x
i
−
1
x
i
−
x
i
−
1
x
∈
[
x
i
−
1
,
x
i
]
x
−
x
i
+
1
x
i
−
x
i
+
1
x
∈
[
x
i
,
x
i
+
1
]
0
x
∉
[
x
i
−
1
,
x
i
+
1
]
l_i(x)=\begin{cases} \frac{x-x_{i-1}}{x_{i}-x_{i-1}} & x\in [x_{i-1},x_{i}] \\ \frac{x-x_{i+1}}{x_{i}-x_{i+1}} & x\in [x_{i},x_{i+1}] \\ 0 & x\notin [x_{i-1},x_{i+1}] \\ \end{cases}
li(x)=⎩
⎨
⎧xi−xi−1x−xi−1xi−xi+1x−xi+10x∈[xi−1,xi]x∈[xi,xi+1]x∈/[xi−1,xi+1]
默认采用分段线性插值
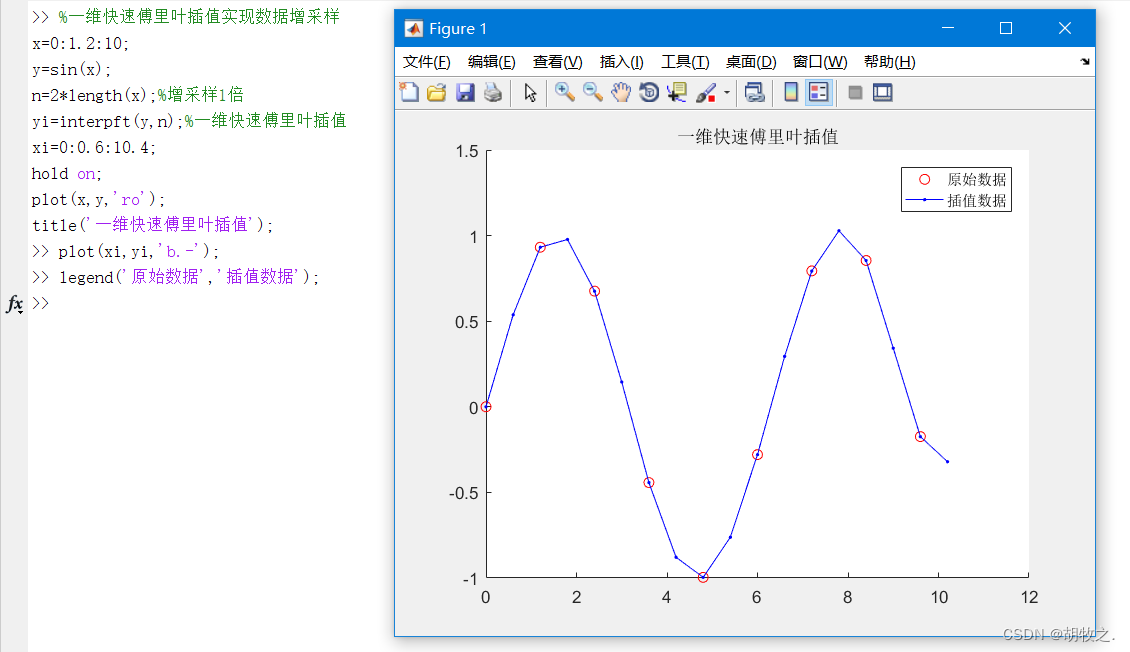
2.一维快速傅里叶插值(interpft)
一维快速傅里叶插值通过函数
i
n
t
e
r
p
f
t
(
)
interpft()
interpft()来实现,该函数用傅里叶变换把输入数据变换到频域,然后用更多点的傅里叶逆变换变回时域,其结果是对数据进行增采样
interpft()调用格式如下:
y=interpft(x,n) 对x进行傅里叶变换,然后使用n点傅里叶逆变换变回到时域
如果x是一个长度为m、采样间隔为dx的向量,则数据y的采样间隔就是mdx/n,要注意n不能小于m
如果x是矩阵,对x的列进行插值操作,返回一个矩阵y,y与x列数相同,但y有n行
y=interpft(x,n,dim) 在dim指定的维度上进行操作
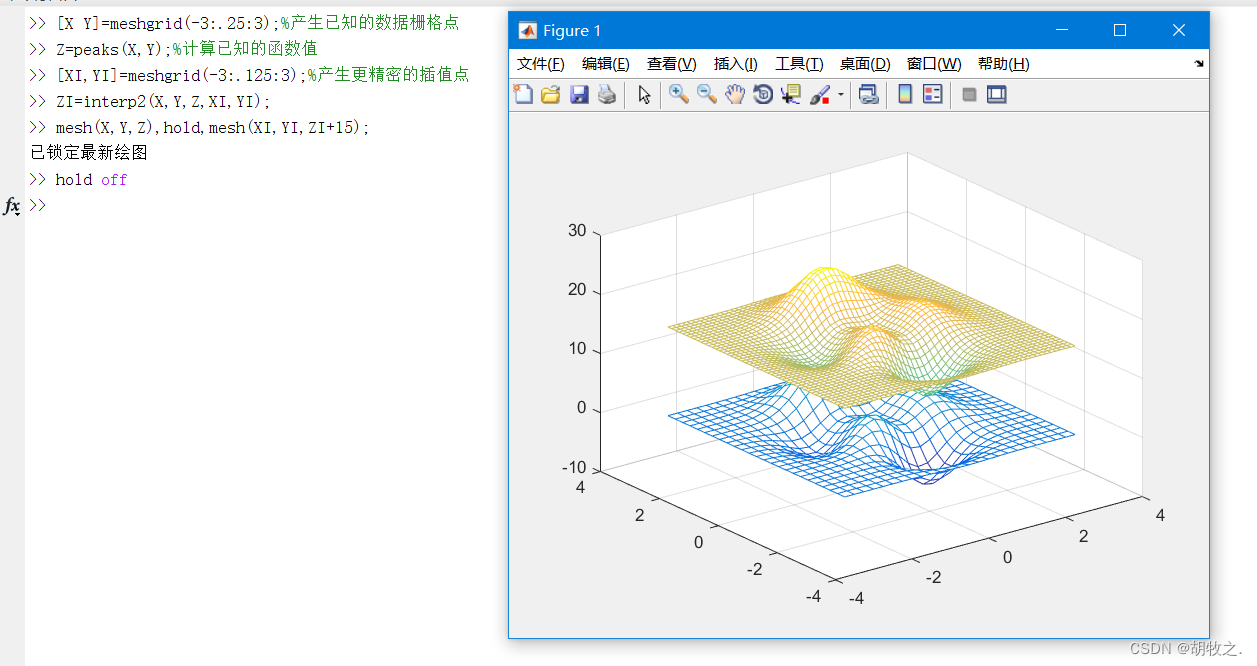
(三)二维插值
当被插值函数y=f(x)为二元函数时,为二维插值,MATLAB中使用interp1函数实现一维插值,其调用格式如下:
Vq=interp2(X,Y,V,Xq,Yq,METHOD) XYV是相同大小的矩阵,V(i,j)是数据点[X(i,j),Y(i,j)]上的函数值;Xq、Yq是待插值数据网格,Method为插值方法
插值方法与一维插值特点类似,具体实现上有变化

三、函数极限
(一)极限概念
设
{
x
n
}
\{x_n\}
{xn}为数列,
a
a
a为常数。若对任给的正数
ε
\varepsilon
ε,总存在正整数
N
N
N,使得当
n
>
N
n>N
n>N时有
∣
x
n
−
a
∣
<
ε
|x_n-a|<\varepsilon
∣xn−a∣<ε,则称数列
{
x
n
}
\{x_n\}
{xn}收敛于
a
a
a,常数
a
a
a称为数列
{
x
n
}
\{x_n\}
{xn}的极限,并记作:
lim
n
→
+
∞
x
n
=
a
\lim\limits_{n \rightarrow +\infty} x_n=a
n→+∞limxn=a
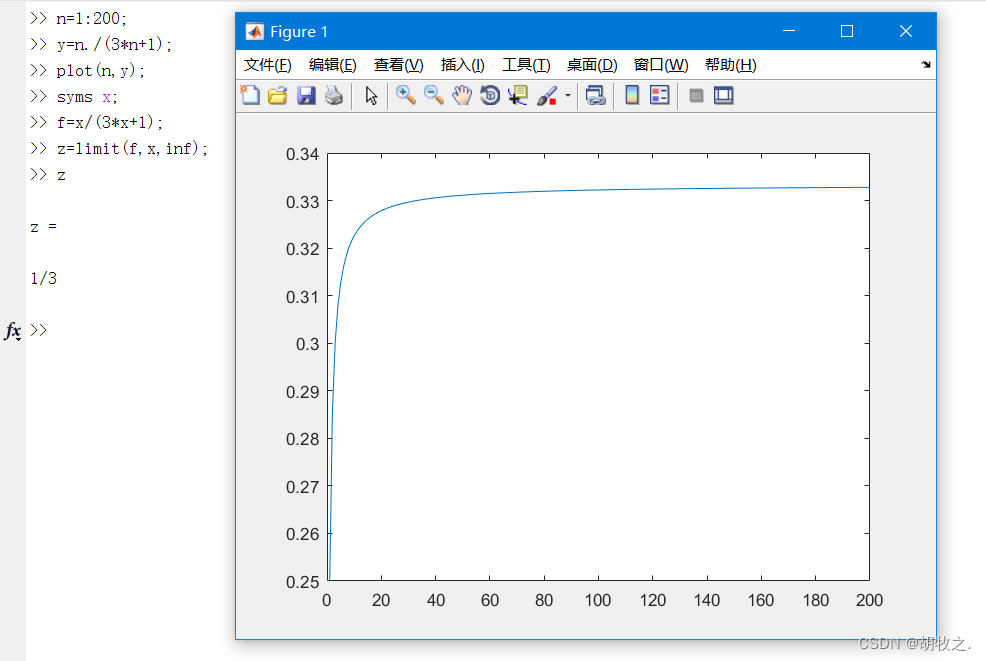
(二)求极限的函数 limit()

在MATLAB中采用limit函数求某个具体函数的极限,其常用的调用格式如下:


syms在matlab中的作用是:定义符号变量。
四、函数数值积分
定积分的计算可用牛顿-莱布尼茨公式:
∫
a
b
f
(
x
)
d
x
=
F
(
b
)
−
F
(
a
)
\int_a^bf(x)dx=F(b)-F(a)
∫abf(x)dx=F(b)−F(a)
其中
F
(
x
)
F(x)
F(x)是
f
(
x
)
f(x)
f(x)的原函数之一,可用不定积分求出
但在实际应用上述公式时,却有一系列问题

数值积分便是为了解决上述问题而提出来的,数值积分只需计算
f
(
x
)
f(x)
f(x)在节点
x
i
(
i
=
1
,
2
,
.
.
,
n
)
x_i(i=1,2,..,n)
xi(i=1,2,..,n)上的值,计算方便且适合在计算机上实现
(一)数值积分问题的数学表述
区间
[
a
,
b
]
[a,b]
[a,b]上的定积分
∫
a
b
f
(
x
)
d
x
\int_a^bf(x)dx
∫abf(x)dx,就是在区间
[
a
,
b
]
[a,b]
[a,b]内取
n
+
1
n+1
n+1个点
x
0
,
x
1
,
.
.
.
,
x
n
x_0,x_1,...,x_n
x0,x1,...,xn利用被积函数
f
(
x
)
f(x)
f(x)在这
n
+
1
n+1
n+1个点的函数值的某一种线性组合来近似作为待求定积分的值,即
∫
a
b
f
(
x
)
d
x
≈
∑
k
=
0
n
A
k
f
(
x
k
)
\int_a^bf(x)dx \approx \sum_{k=0}^nA_kf(x_k)
∫abf(x)dx≈k=0∑nAkf(xk)
其中,
x
k
x_k
xk称为积分节点,
A
k
A_k
Ak称为求积系数,右端公式称为左端定积分的某个数值积分公式
因此,求积分的关键在于积分节点
x
k
x_k
xk的选取及积分系数
A
k
A_k
Ak的确定
MATLAB支持三重以下的积分运算
(二)一元函数的数值积分 quad/quadl/quadv
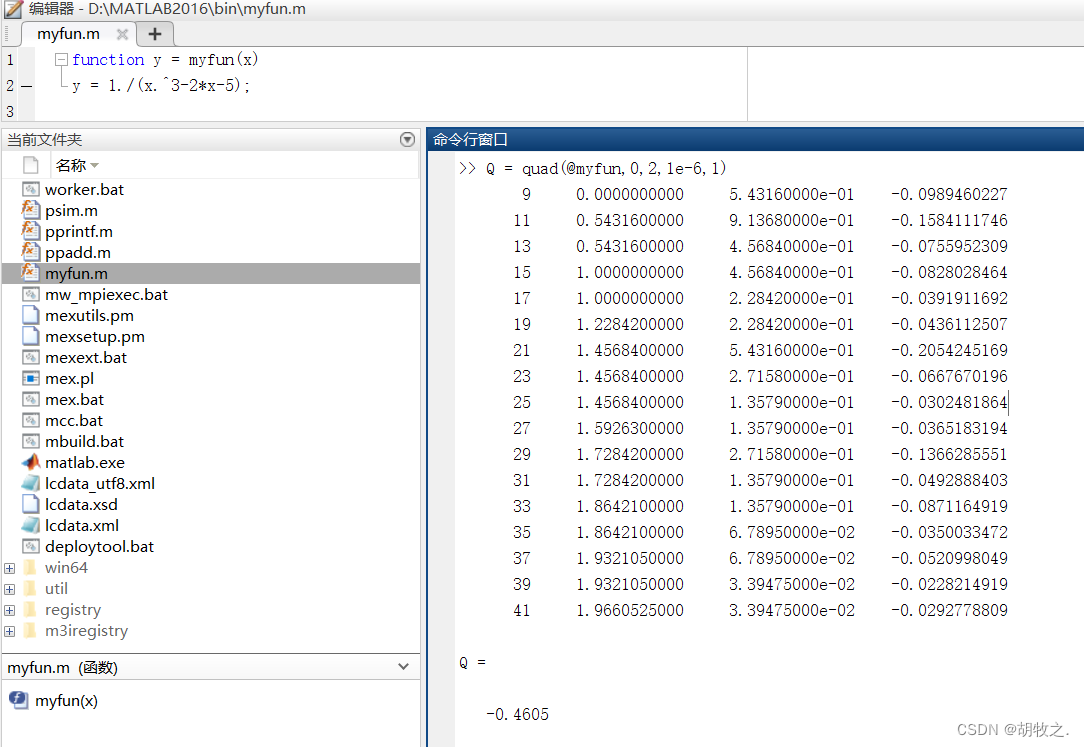
1.quad函数
quad采用遍历的自适应辛普森(Simpson)法计算函数的数值积分,适用于精度要求低、被积函数平滑性较差的数值积分,常用调用格式如下:
q = quad(fun,a,b) fun为函数句柄,fun应接收向量输入并返回相同长度的向量;a与b为积分起始值与结束值
q = quad(fun,a,b,tol) tol默认为1e-6,tol增大可以加快计算速度,但有损计算精度
q = quad(fun,a,b,tol,trace) trace非零时,展示计算过程中的[fcnt,a,b-a,q],fcnt表示函数计算次数
[q,fcnt] = quad(...)
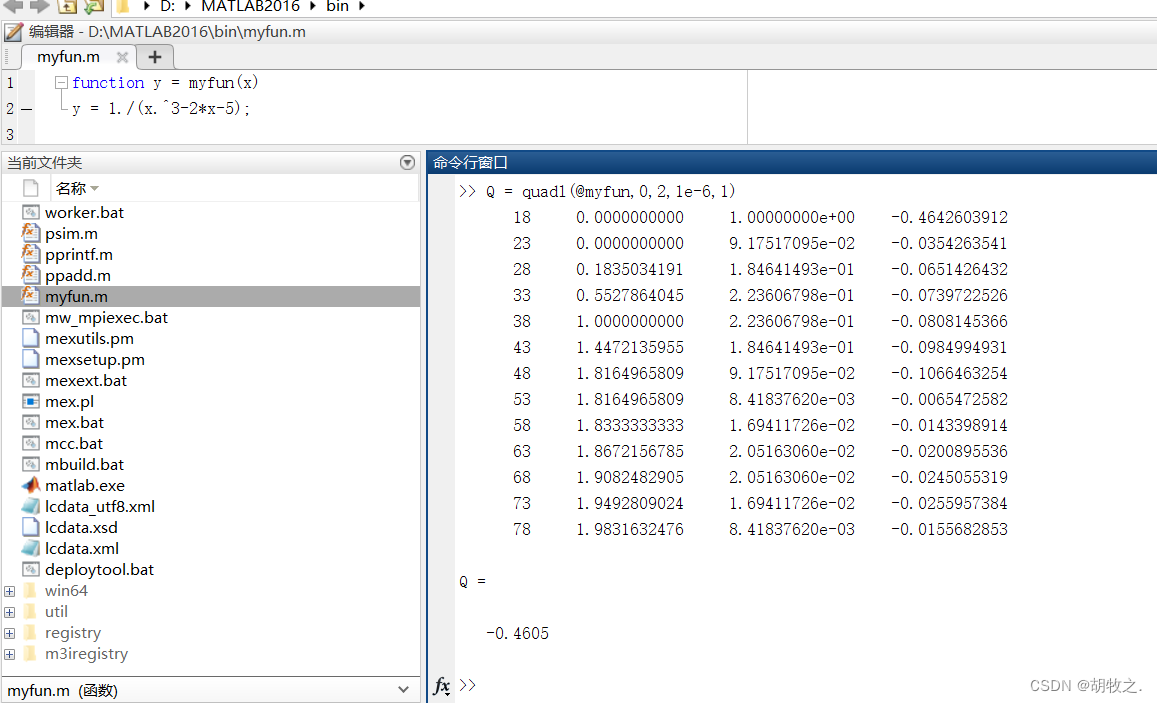
2.quadl函数
quadl采用遍历的自适应Lobatto法计算函数的数值积分,适用于精度要求高、被积函数曲线比较平滑的数值积分,常用调用格式与quad一致
通常quad函数具有较快的计算速度,但准确性较差;而quadl函数较慢却准确度较高
3.quadv函数
quadv函数是quad函数的矢量扩展,因此也称为矢量积分,可以一次计算多个一元函数的数值积分值
其用法与quad函数一致,不过矢量积分的返回结果是一个向量
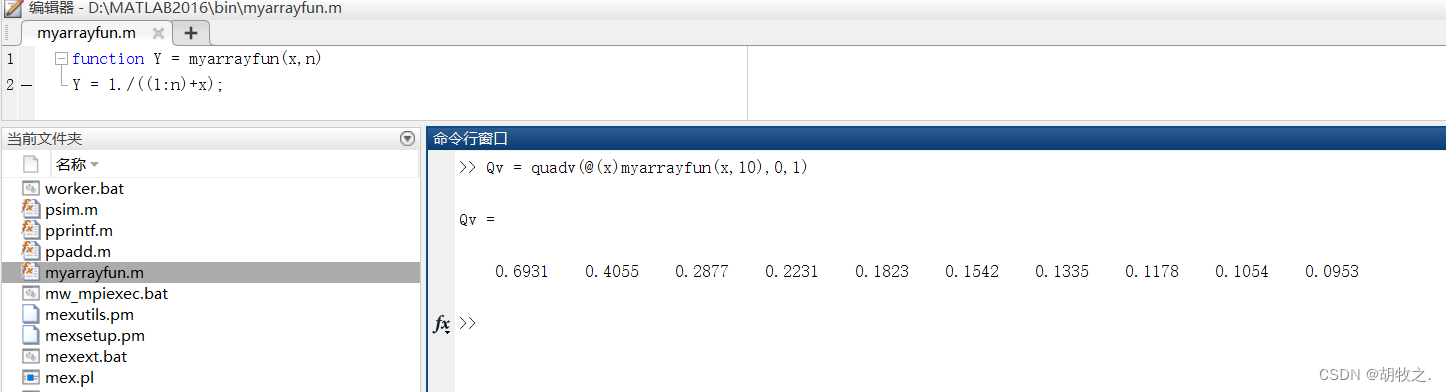
上图就是同时计算了10个函数的数值积分值
(三)多重数值积分 dblquad/triplequad
1.二重数值积分计算函数 dblquad
d
b
l
q
u
a
d
dblquad
dblquad函数可以计算在矩形区域
x
∈
[
x
m
i
n
,
x
m
a
x
]
,
y
∈
[
y
m
i
n
,
y
m
a
x
]
x\in[x_{min},x_{max}],y\in[y_{min},y_{max}]
x∈[xmin,xmax],y∈[ymin,ymax]内的数值积分值
调用格式如下:
q = dblquad(fun,xmin,xmax,ymin,ymax)
q = dblquad(fun,xmin,xmax,ymin,ymax,tol) tol默认为1e-6
q = dblquad(fun,xmin,xmax,ymin,ymax,tol,method) method表示指定计算一维积分时用的方法,默认为quad,@quadl表示采用quadl
也可为用户自己编写的函数的函数句柄,但要保证调用序列与quad一致

2.三重数值积分计算函数 triplequad
t
r
i
p
l
e
q
u
a
d
triplequad
triplequad函数可以计算在空间区域
x
∈
[
x
m
i
n
,
x
m
a
x
]
,
y
∈
[
y
m
i
n
,
y
m
a
x
]
,
z
∈
[
z
m
i
n
,
z
m
a
x
]
x\in[x_{min},x_{max}],y\in[y_{min},y_{max}],z\in[z_{min},z_{max}]
x∈[xmin,xmax],y∈[ymin,ymax],z∈[zmin,zmax]内的数值积分值
调用格式如下:
q = triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax)
q = triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol)
q = triplequad(fun,xmin,xmax,ymin,ymax,zmin,zmax,tol,method)
参数含义与dblquad一致























 1549
1549











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








