算法设计与分析学习：第二章递归与分治算法

迟迟迟迟迟子

已于 2022-10-22 15:49:41 修改

阅读量662

点赞数

分类专栏：算法设计与分析学习文章标签：算法学习数据结构

于 2022-10-21 21:53:34 首次发布

本文链接：https://blog.csdn.net/qq_52641289/article/details/127441439

版权

算法设计与分析学习专栏收录该内容

3 篇文章 0 订阅

订阅专栏

第二章递归与分治算法
算法思路+时间复杂度分析+实现代码（可能会写吧，不确定）

1.分治法思想

分治法就是把一个规模为n的大问题分解成k个规模为n/m的子问题，然后再合并，那么这个大问题的算法时间复杂度为：
T(n)=k*T(n/m)+f(n)
注：f(n)是指将k个规模为n/m的子问题合并时的时间复杂度

关于这个T(n)具体怎么解，后面会记录

2.二分搜索技术

2.1题目描述

要在一个排好序的数组a[0:n-1]寻找特定元素x

2.2算法思路

将n个元素分成个数大致相同的两半，取a[n/2]与x作比较，如果x=a[n/2]，则找到x，算法终止。如果x<a[n/2]，则只在数组a的左半部分继续搜索x；如果x>a[n/2]，则只在数组a的右半部分继续搜索x。

2.3伪代码

template<class Type>
int BinarySearch(Type a[],int n,Type x)
{
	int low=0;
	int high=n-1;
	while(low<=high)
	{
		int mid=(low+high)/2;
		if(a[mid]==x)
			return mid;
		else if(a[mid]<x)
			high=mid-1;
		else
			low=mid+1;
	}
	return -1;//如果没找到
}

2.4时间复杂度分析

根据上面的伪代码，可以看出，时间复杂度最高的应该是在while循环内，但是由于每次都是折半查找，假设查找次数是y，相当于y次才能找到元素x的索引。那么2^y=n，所以y=logn。所以时间复杂度为O(logn)

3.大整数的乘法

3.1题目描述

两个n位的大整数相乘

3.2算法思路

将两个大整数X，Y都分成两份，每段n/2位，这样就变成了四个n/2位的数字
X=A×2^(n/2)+B
Y=C×2^(n/2)+D
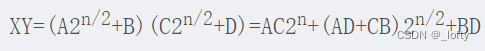
XY=(A2n/2+B)(C2n/2+D)=AC2n+(AD+CB)2n/2+BD
这样就把两个n位的大整数乘法分解成了四个n/2位的（？稍小一点的）大整数乘法。
（后面可以再把这四个稍小一点的大整数乘法再分成n/2位的再小一点的大整数乘法，其实就是递归调用自身啦）

3.3时间复杂度初步分析

在上面的分析中看到，规模为n的原问题，被分解成了4个规模为n/2的子问题，而合并，即先乘以对应的2的幂再将这些分解的乘法得出的结果相加，需要花费O(n)的时间。
注：我之前一直以为是O(1)，因为我觉得加法很简单，乘以2的幂也很简单，用一个pow函数不就完了？结果看书上写的是这些操作算法复杂度为O(n)，我大受震撼，问了同学才明白，这个加法又不是简单的加法，这个加法是大整数加法啊！就算它位数已经变成n/2，那也还是大整数啊，而大整数加法是一位一位加的，所以是O(n)

那么这个算法复杂度可以这样表示：
T(n)=4T(n/2)+O(n)

T(n)该怎么算呢？
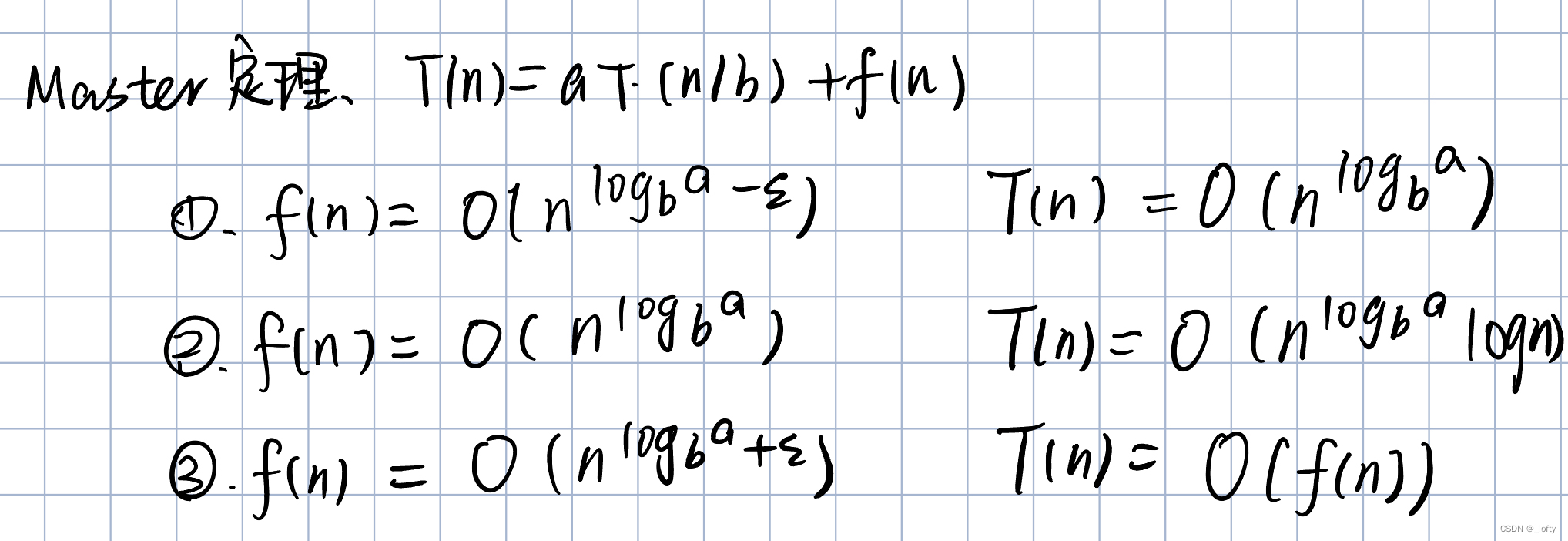
请添加图片描述
这里的f(n)=O(n)，也就是第一种情况，所以T(n)=O(n^2)
这个复杂度其实也没有很好……就寻思能不能再改改。那么其实最需要改的就是乘法了，这里是四个乘法，能不能再减少点乘法呢？

3.4时间复杂度进一步分析

再观察一下这个式子
能不能把AD和CB也用AC和BD来表示呢？
这样就只用算两次乘法了呀
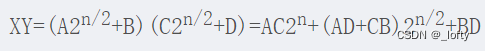
在这里插入图片描述
那必定是可以的

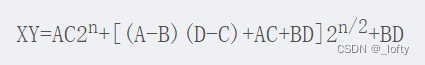
这个是怎么解出来的呢？因为交叉项中有AD,CB，所以A、D和B、C肯定分别在两个括号里，加还是减就随便了，都能凑出来

那么到现在为止，已经简化到只有三个大整数乘法了，于是时间复杂度就变为
T(n)=3T(n/2)+O(n)
按照上面的计算公式可得到
T(n)=O(n^log3)

4.合并排序

4.1题目描述

对一个无序的数组进行排序

4.2算法思路

将数组分为两个大小大致相同的两个子集合，分别对两个子集合进行排序，最终将两个排好序的子集合合并成要求的集合

4.3伪代码

template<class Type>
void MergeSort(Type a[],int low,int high)
{
	if(low<=high)
	{
		int mid=(low+high)/2;
		MergeSort(a,low,mid);
		MergeSort(a,mid+1,high);
		Merge(a,b,low,mid,high);
		copy(a,b,low,high);
	}
}

4.4时间复杂度分析

很明显，一个规模为n的问题被分解成了2个子问题，而这两个子问题规模为n/2，将这两个子问题合并需要花费O(n)的时间。
注：这里的合并包括了将两个已经排好序的数组重新排成一个数组和将重新排好的数组复制回原数组。
其中，两个已经排好序的数组合并为一个数组，在数据结构与算法中已学习过，即两个指针分别指向两个数组，向右扫描，遇到小的就放进新数组，向右移一位，大的就不移动指针，所以时间复杂度为O(n)；而复制数组也只需要花费O(n)的时间。所以合并一共只花费O(n)的时间。

故合并排序算法时间复杂度为：
T(n)=2T(n/2)+O(n)

经过前面公式的计算可得
T(n)=O(nlogn)

5.快速排序

5.1题目描述

同上，对a[p:r]的子数组进行排序

5.2算法思路

①分解：以a[p]为基准，将a[p:r]分解成三段，分别是a[p:q],a[q],a[q+1:r]，左边子数组全部都小于a[q]，右边子数组全部大于a[q]，而q在划分的结束后决定
②递归求解：对左边子数组和右边子数组递归
③合并：不用合并，就地排序，不像合并排序，没有利用辅助数组

5.3伪代码

template<class Type>
QuickSort(Type a[],int p,int r)
{
	if(p<r)
	{
		int q=partition(a,p,r);
		QuickSort(a,p,q-1);
		QuickSort(a,q+1,r);
	}
}

template<class Type>
void partition(Type a[],int p,int r)
{
	int i=p;
	int j=r+1;
	Type x=a[p];
	while(i<=j)
	{
		while(a[++i]<x&&i<r);
		while(a[--j]>x&&j>p);
		swap(a[i],a[j]);
	}
	a[p]=a[j];
	a[j]=x;
	return j;
}

5.4时间复杂度分析

该算法因为不需要合并，但是在处理两个子问题之前，还需要进行partition，而partition算法时间复杂度为O(n)。
注：因为左右指针一起往中间扫描，加起来，相当于只遍历了数组一遍
所以快速排序的时间复杂度为：
T(n)=2T(n/2)+O(n)
解得T(n)=O(nlogn)
注：这是在最好情况下！！！就是对半分

而在最坏情况下（就是每次都只分成，1，1，n-2）
T(n)=T(n-1)+O(n)
解得T(n)=O(n^2)，这是高中数列的知识，递归算一下就行

结合最好情况和最坏情况，最终时间复杂度为
T(n)=O(nlogn)

6.线性时间选择

6.1题目描述

一个集合有n个元素和一个整数k，要求找出这n个元素中，第k小的元素。

6.2算法思路

①将n个元素划分成n/5组，每组5个元素。
②对每组组内五个元素进行排列，取出每组的中位数，也就是第三个数。
③对每组的中位数进行递归调用Select，找出这些中位数的中位数。
④调用partition算法，以该数为基准，将小于该数的所有数放在左边，将大于该数的所有数放在右边，最后返回基准数的index
⑤比较index与k的关系，如果index<k，则递归右边；如果index>=k，则递归调用左边

6.3伪代码

template<class Type>
Type Select(Type a[],int p,int r,int k)
{
	if(r-p<=75)
	{
		sort(a,p,r);
		return a[p+k-1];
	}
	for(int i=0;i<n/5;i++)
		swap(a[p+i*5+2],a[p+i]);//将a[p+5*i]到a[p+5*i+4]的第三小元素与a[p+i]进行交换
	Type x=Select(a,p,p+(r-p-4)/5,(r-p-4)/10)//找中位数的中位数 注①②
	int i=Partition(a,p,r,x);//将小于x的数放在左边，大于x的数放在右边，然后返回中位数的中位数的下标
	int j=i-p+1;//左半部分的长度
	if(k<=j)
		return Select(a,p,i,k);
	else
		return Select(a,i+1,r,k-j);
}

关于代码的一些解释：
①Select函数的第三个参数：因为我们这里要求的是中位数的中位数，而Select函数要求传入的是数组的左边界，右边界，以及要查第几大。于是我们需要求出中位数一共有多少个。
很显然，中位数的个数为(r-p+1)/5，其中的r-p+1是所有元素的个数。算出个数之后需要计算右边界（个数并不等于右边界！）所以右边界的索引值为：p+长度-1=p+(r-p+1)/5-1=p+(r-p-4)/5
②Select函数的第四个参数：要查中位数的索引，其实就是（个数-1）/2，所以第四个参数k为：(（r-p+1）/5-1)/2=(r-p-4)/10

6.4时间复杂度分析

假设使用Select算法解决整个问题需要花费T(n)，那么使用Select算法找中位数的中位数x，需要花费T(n/5)的时间。而使用Select算法找左边或者找右边，最多需要花费T(3n/4)的时间。
注：为什么这里是3n/4呢？因为在整个数组中，至少有3*（(（n/5-1）)/2）个数大。这是因为n/5是总的中位数个数，把自己这个中位数的中位数减了，再除以2，就是左边中位数的个数，乘以三是因为每组都有三个小于x
在n>=75的时候，3*（(（n/5-1）)/2）>=n/4，所以每次至少都能砍掉(1/4)n，于是最坏的就是T(3n/4)
那么时间复杂度可以表示为：
T(n)<=C1 n<75
C2n+T(n/5)+T(3n/4) n>=75
递归解得T(n)=O(n)