数学形态学图像处理：用“形状手术刀”解剖图像的秘密-CSDN博客

本文链接：https://blog.csdn.net/qq_53529450/article/details/146253395

一、数学形态学是什么？——给图像做“形状手术”

想象你有一块形状不规则的岩石，想研究它的内部结构。数学形态学就像一把精密的“手术刀”，用不同形状的“探针”（结构元素）在图像上滑动，通过切割、填补等操作，揭示物体最本质的结构特征。它的核心思想是：用形状对抗形状，通过结构元素与图像的相互作用，过滤无关噪声，提取关键信息。

举个栗子：用圆形探针在图像上滚动，可以磨平小尖刺；用十字形探针扫描，能连接断裂的线条。就像用不同形状的模具去“盖章”，保留符合模具的特征。

二、二值形态学：黑白世界的“加减法”

二值图像只有0（黑）和1（白），形态学操作像做“形状的加减法”：

腐蚀（Erosion）：削去边缘
- 操作：结构元素必须完全“嵌入”目标区域，保留中心点。
- 效果：瘦身、去毛刺。比如消除证件照边缘的噪点。
- 比喻：用橡皮擦沿着物体边缘擦除一圈。

膨胀（Dilation）：填补缺口
- 操作：结构元素与目标区域有交集，则扩展中心点。
- 效果：增肥、补空洞。比如修复老照片中的断裂文字。
- 比喻：用画笔沿物体边缘描粗一圈。

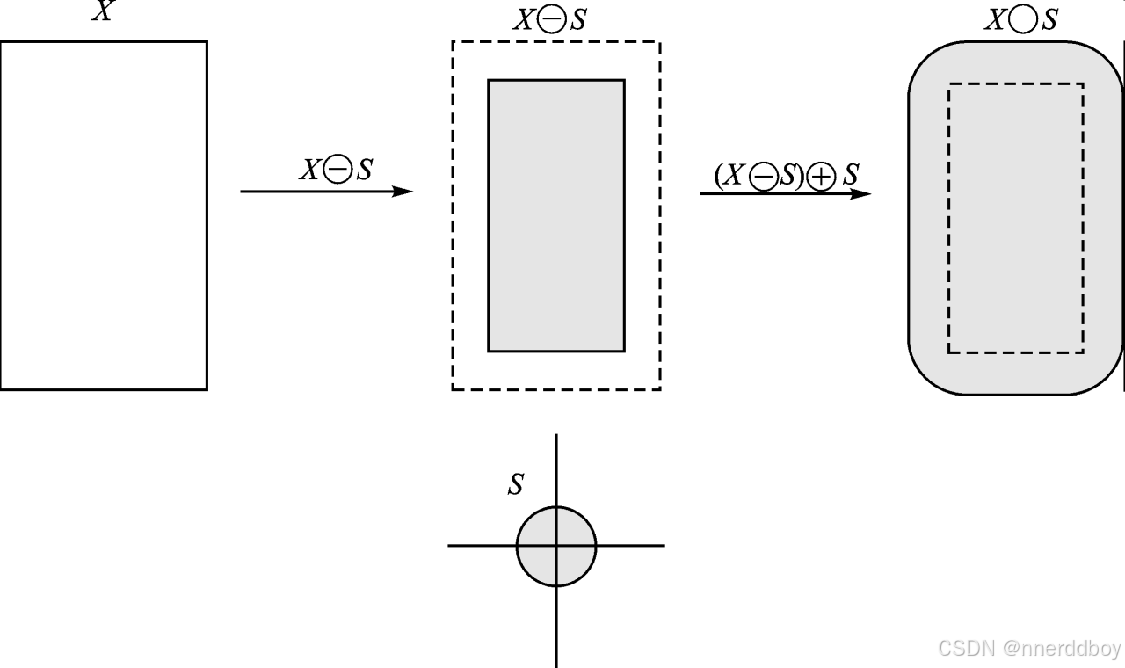
开运算（先腐蚀后膨胀）：去刺不伤身
- 效果：平滑轮廓，去除孤立小点，保留主体形状。
- 场景：去除显微镜图像中的散落细胞杂质。
闭运算（先膨胀后腐蚀）：补洞不变形
- 效果：填充细小孔洞，弥合裂缝。
- 场景：修复卫星地图中道路的断裂处。

三、灰度形态学：明暗世界的“地形改造”

灰度图像像起伏的“地形图”，形态学操作变为对亮度值的局部改造：

灰度腐蚀：削平“山峰”
- 操作：用结构元素（如半球）从图像下方滑动，每个位置取最小值。
- 效果：暗化亮区域，抑制高光噪点。例如消除X光片中的亮点噪声。

灰度膨胀：填平“山谷”
- 操作：结构元素从图像上方滑动，取最大值。
- 效果：亮化暗区域，填补阴影。例如增强夜视图像中的暗部细节。

灰度开/闭运算：选择性滤波
- 开运算：先削峰后填谷，去除亮噪点（如扫描文档中的白点）。
- 闭运算：先填谷后削峰，消除暗孔洞（如工业零件图像的表面凹痕）。

如果换成真实图像：

matlab代码如下：

% %% 已知图片
%% 读取并预处理用户图像（路径已替换）
original_img = imread('C:\Users\Lenovo\OneDrive\桌面\医学图像处理相关\代码\class3\Peppers.bmp');
gray_img = im2double(original_img);

% 注意：如果原始图像是RGB格式，请取消下面这行注释
% gray_img = im2double(rgb2gray(original_img));

%% 添加可控噪声（可选）
% gray_img = imnoise(gray_img, 'salt & pepper', 0.02);

%% 结构元素自适应调整
img_size = size(gray_img);
se_radius = round(max(img_size)/100);
se = strel('disk', se_radius);

%% 形态学操作
eroded = imerode(gray_img, se);  
dilated = imdilate(gray_img, se);
opened = imopen(gray_img, se);  
closed = imclose(gray_img, se);

%% 三维可视化布局
figure;

% 原始图像地形
subplot(2,3,1);
surf(gray_img, 'EdgeColor','none', 'FaceLighting','gouraud');
title('原始地形');
view(-25, 65); 
zlim([0 1]);
colormap(flipud(gray));
material dull;

% 腐蚀地形
subplot(2,3,2);
surf(eroded, 'EdgeColor','none');
title('腐蚀：削平亮峰');
view(-25,65); 
zlim([0 1]);

% 膨胀地形
subplot(2,3,3);
surf(dilated, 'EdgeColor','none');
title('膨胀：填充暗谷');
view(-25,65); 
zlim([0 1]);

% 开运算
subplot(2,3,4);
surf(opened, 'EdgeColor','none');
title('开运算：消除亮斑');
view(-25,65); 
zlim([0 1]);

% 闭运算
subplot(2,3,5);
surf(closed, 'EdgeColor','none');
title('闭运算：填补暗洞');
view(-25,65); 
zlim([0 1]);

% 颜色标尺
subplot(2,3,6);
caxis([0 1]); 
colorbar('Location', 'south');
axis off;
title('亮度标尺');

%% 统一坐标轴设置（关键修复）
all_axes = findobj(gcf, 'Type','axes');

% 只处理前5个图像子图（第6个是色标）
set(all_axes(1:5), 'ZTick',[], 'FontSize',8, 'Box','off');

%% 颜色标尺优化
h = findobj(gcf, 'Type', 'colorbar');
h.Position = [0.3 0.05 0.4 0.02];
h.Label.String = '亮度值 (0=黑, 1=白)';

sgtitle('医学图像灰度形态学三维分析','FontSize',14, 'FontWeight','bold');

四、形态学的杀手锏应用

形态学滤波：开闭运算交替使用，实现“双边滤波”。
- 案例：监控视频中，去除动态干扰（如雨雪）同时保留人物轮廓。
骨架抽取（Skeletonization）：提取物体的“中轴线”。
- 算法思想：
  - 烈火模拟：想象从边界点燃火焰，熄灭处即为骨架。
  - 最大内切圆：骨架是无数最大圆盘的圆心连线。
- 应用：手写数字识别（提取笔画骨架）、血管网络分析。
细化（Thinning）：保留连通性，压缩冗余像素。
- 规则：删除不影响连通的边界点。比如OCR处理，将粗体字变为单线骨架。

五、形态学的独特优势

等幂性：一次开运算就能彻底去噪，无需重复（传统滤波需多次迭代）。
结构保护：不像高斯滤波会模糊边缘，形态学能保持物体形状特征。
多尺度分析：通过调整结构元素大小，可分层提取细节（如细胞核与细胞膜分离）。

六、MATLAB实战点睛

核心函数：
- imerode()腐蚀，imdilate()膨胀，imopen()开运算，imclose()闭运算。
- bwmorph()实现骨架抽取（'skel'参数）和细化（'thin'）。
调试技巧：
- 结构元素选择：strel('disk',5)生成圆形探针，半径5像素。
- 可视化中间结果：逐步观察腐蚀、膨胀的效果，避免过度操作。