matalb+yalmip+gurobi初识篇

记录下学习所获得的经验

1. 关于matlab，yalmip和gurobi的关系，通俗点来讲就是：matlab当中可以集成yalmip，而yalmip当中可以添加gurobi优化求解器，yalmip是许多优化求解器的容器，需要先下载yalmip才可以把gurobi添加进去

2. 将yalmip放入matlab的工具箱当中之后，可以输入yalmiptest查询一下是否安装成功，或者查看当前已经安装的优化求解器。

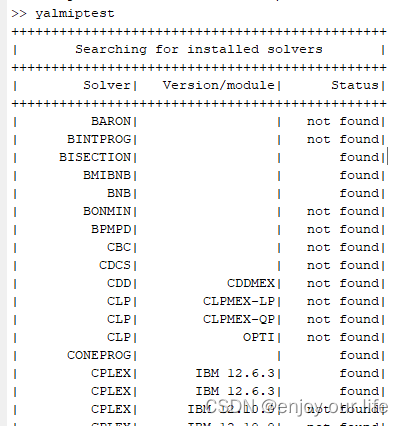
当gurobi添加完成之后，就到了编写代码的阶段了，代码的组成结构特别简单，共分为5大步骤：

1. 定义变量阶段：sdpvar:实数变量,intvar:整数变量，binvar:0-1变量

% 定义变量:sdpvar:实数变量（可以是小数）,intvar:整数变量，binvar:0-1变量

% 拿机器调度为例，n是任务的个数，m是机器个数，即把n个任务合理的分配到m个机器上运行

% 定义任务开始时间与完成时间的决策变量
% 开始时间的定义为n*1的列向量，表示每个任务开始执行的时间，可以是小数类型的量
start_time = sdpvar(n, 1, 'full');
fin_time = sdpvar(n, 1, 'full');


% intvar，就是定义的变量当中元素只能是整数



% 任务安排，如果x(i,j)==1则表示任务i在任务j上运行
% 为什么我定义x(i,j)==1则表示任务i在任务j上运行，这是与后面的具体约束有关系的，这是人为规定的
x = binvar(n,m,'full');


% 定义辅助变量z表示两个任务是否在同一个处理器上执行
% 如果z（i，j，k）=1则表示任务i和j都在k机器上运行
z = binvar(n, n, m, 'full');

2. 写约束阶段

经验：约束 约束的是第一步当中定义变量当中的量值，即要约束当中的量值具体在哪个区间当中

例如：

% 定义约束条件
% 机器安排的约束, 表示每个任务只能在一个机器上运行


Constraints = [];


for i = 1 : data.n
    Constraints = [Constraints, sum(x(i,:)) == 1];
end

一定要加上，空约束集合：Constraints = [];

利用for循环写约束是很有用的

sum很有用

.* 点乘也很有用

Constraints = [Constraints,...............] 添加约束

每一次循环表示：x的每一行元素相加都恒等于1，又因为x定义为0-1变量，这不就恰好说明了x的每一行都只能有一个1（每个任务只能在一个机器上运行）

3. 目标函数阶段

fit = 你的计算过程即可

4. 调用gurobi，或者其他的优化求解器，非常简单

% 选择求解器

ops = sdpsettings('solver','gurobi','verbose',2);
result = optimize(Constraints,fit,ops);




% 如果想调用cplex
ops = sdpsettings('solver','cplex','verbose',2);
result = optimize(Constraints,fit,ops);

5. 查看得到最优解具体的值

% 这里的x等都是前面定义的变量
value_x = value(x);
value_start_time = value(start_time);
value_fin_time = value(fin_time);


% 想打印出来也行，不想打印就在matlab的工作区当中查看
disp(value(x))
disp(value(y))
disp(value(f))
disp(value(f_1))

总结代码：

% 1
% 定义变量:sdpvar:实数变量,intvar:整数变量，binvar:0-1变量

% 任务安排，x(i,j)==1表示任务i在任务j上运行
x = binvar(n,m,'full');

% 定义任务开始时间与完成时间的决策变量
start_time = sdpvar(n, 1, 'full');
fin_time = sdpvar(n, 1, 'full');

% 定义辅助变量z表示两个任务是否在同一个处理器上执行
z = binvar(n, n, m, 'full');


% 2
Constraints = [];
% 定义约束条件
% 机器安排的约束, 表示每个任务只能在一个机器上运行

for i = 1 : data.n
    Constraints = [Constraints, sum(x(i,:)) == 1];
end


for i = 1:data.n
    Constraints = [Constraints, fin_time(i) <= cmax];
end
for i = 1:data.n
    Constraints = [Constraints, fin_time(i) >=0];
end


% 目标函数当中的量值可以写到约束当中，这样更简单
for i = 1:data.n
    Constraints = [Constraints, e_1(i) == px_cmk(i) * ct_time(i)] ;
end
for i = 1:data.m
    Constraints = [Constraints, e_0(i) == max(fin_time) * data.pks(i)];
end


% 3
% 写目标函数
fit = sum(e_0) + sum(e_1);




% 4 
% % 选择求解器
ops = sdpsettings('solver','cplex','verbose',2);
% % 调用cplex求解目标函数,求最小值
optimize(Constraints,fit,ops)



ops = sdpsettings('solver','gurobi','verbose',2);
result = optimize(Constraints,fit,ops);



% 5
% 查看具体值
value_x = value(x);
value_y = value(y);
value_start_time = value(start_time);
value_fin_time = value(fin_time);
% disp(value(x))
% disp(value(y))
% disp(value(f))
% disp(value(f_1))

具体写约束和目标函数当中会出现很多问题，不知道是不是yalmip自己的原因，各种报错，下篇再写