关于图着色问题（GCP）的优化算法及启发式算法求解过程——沐雨先生

一、题目

图着色问题的优化算法设计和启发式算法设计，以及对结果进行必要的分析，用Python绘图，并对结果进行文字说明。

二、问题描述

图着色问题（Graph Coloring Problem, GCP）又称着色问题，是最著名的NP-完全问题之一。
数学定义：给定一个无向图G=（V, E），其中V为顶点集合，E为边集合，图着色问题即为将V分为K个颜色组，每个组形成一个独立集，即其中没有相邻的顶点。其优化版本是希望获得最小的K值。
数学模型：


实际问题：
①图的m可着色判定问题
给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色。是否有一种着色法使G中每条边的2个顶点着不同颜色。
②图的m可着色优化问题
若一个图最少需要m种颜色才能使图中每条边连接的2个顶点着不同颜色，则称这个数m为该图的色数，即求m。

问题示例：不邻接植花（力扣1042题）
有 n 个花园，按从 1 到 n 标记。另有数组 paths ，其中 paths[i] = [xi, yi] 描述了花园 xi 到花园 yi 的双向路径。在每个花园中，你打算种下四种花之一。另外，所有花园最多有3条路径可以进入或离开。你需要为每个花园选择一种花，使得通过路径相连的任何两个花园中的花的种类互不相同。以数组形式返回 任一可行的方案作为答案 answer，其中 answer[i] 为在第 (i+1) 个花园中种植的花的种类。花的种类用 1、2、3、4表示。保证存在答案。
示例 1：
输入：n = 3, paths = [[1,2],[2,3],[3,1]]
输出：[1,2,3]
解释：
花园 1 和 2 花的种类不同。
花园 2 和 3 花的种类不同。
花园 3 和 1 花的种类不同。
因此，[1,2,3] 是一个满足题意的答案。其他满足题意的答案有 [1,2,4]、[1,4,2] 和 [3,2,1]

三、设计过程

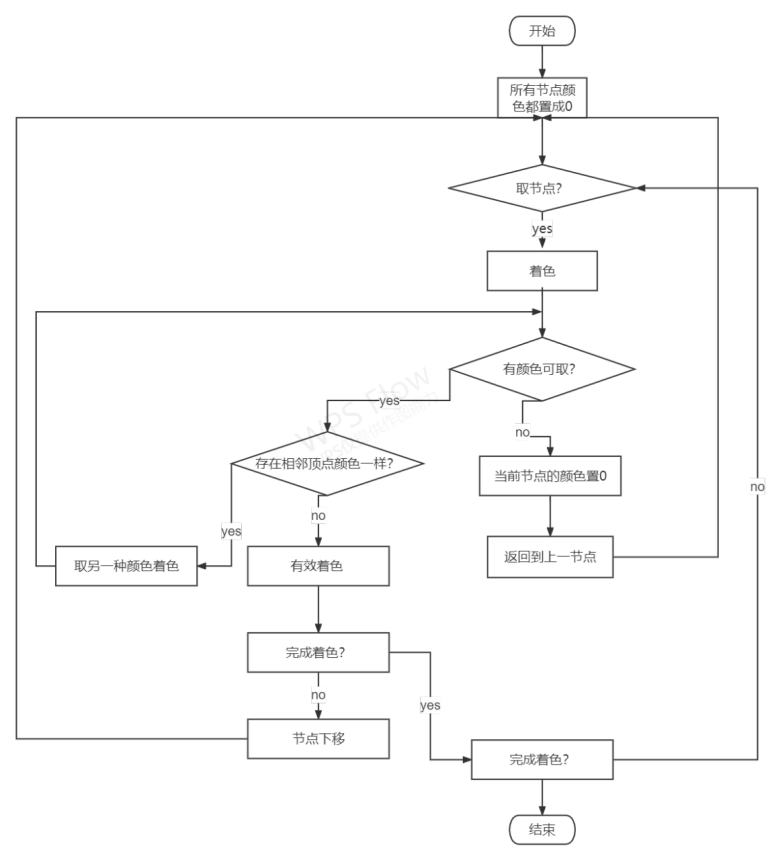
优化算法（回溯法）

·设计思路：回溯法的本质其实就是一种蛮力法，只是通过一定的方法可以使得蛮力法中的一些基本情况可以提前排除从而提高蛮力算法效率，回溯可以理解为排除这些不满足条件的基本情况的过程。
·基本步骤
针对所给问题，定义问题的解空间。
确定易于搜索的解空间结构。
以深度优先方式搜索解空间，并在搜索过程中用剪枝函数避免无效搜索。
·思路过程
1.将上述无向图转换为邻接矩阵Graph，并根据四色定理定义颜色数量m为4。
2.由深度优先搜索解空间树，方法如下：
a) 取结点，并为结点上色。
b) 判断当前结点的颜色是否为有效颜色（即不和相邻的顶点颜色一样）。
c) 若为有效颜色，则按深度优先取下一个结点。
d) 若为无效颜色，则换下一个颜色继续进行b步骤。
e) 若所有颜色都为无效颜色，将当前结点颜色置为0，并回溯到上一个结点，进行a步骤。
f) 当找到了一个解后，令全局变量sum值加一，并通过回溯搜索下一个解。
g) 重复上述步骤，直到所有解被找到。
3.输出所有的解以及统计解的个数。

·示例着色过程

如图
①给顶点A着色a，由于是第一个顶点，所以一定不发生冲突。
②给顶点B着色a，和A顶点发生冲突，因此换为下一种颜色b，此时不发生冲突，因此最终给B着色b。
③给顶点C着色a，和A顶点发生冲突；给顶点C着色b，和B顶点发生冲突，因此给C顶点着色下一种颜色c，此时不发生冲突，因此最终给C着色c。
④给顶点D着色c，不发生冲突，因此最终给D着色c。
⑤给顶点E着色a，与D发生冲突；给顶点E着色b，与B发生冲突；给顶点E着色c，与C发生冲突，给顶点E着色下一种颜色d，此时不发生冲突，因此最终给E着色d。
此时所有顶点都完成着色，也就是确定了一个可行解（abcad，4种颜色），开始回溯过程。
⑥回到顶点D，由于其在上一个可行解中着色为a，因此本次对其着色为a的下一种颜色b，与B发生冲突，因此将其着色为再下一种颜色c，此时不发生冲突，因此最终将其着色为c。
⑦给顶点E着色a，不发生冲突，因此最终将顶点E着色为a。再次得到一组可行解（abcca，3种颜色）。由于该可行解使用的颜色比上一组可行解更少，因此将最优解更新为3。
⑧进行回溯：由于结点C和D的着色都是当前3种颜色中序号最大的颜色c，因此回溯到B结点，将其着色改为c。
⑨对C结点着色c，与B结点冲突，想要换为下一种颜色，但是当前只有3种颜色，因此判断算法终止，全局最优解即为3种颜色。
·算法设计流程图：

·用例无向图

·源代码

import numpy as np
import random
from pathlib import Path
import matplotlib.pyplot as plt
from matplotlib.pyplot import MultipleLocator#从pyplot导入MultipleLocator类，这个类用于设置刻度间隔
plt.rcParams['font.sans-serif'] = ['SimSun']
# 顶点个数
V = 5
# 颜色种类
m = 4
# 邻接矩阵
Graph = np.array([[0, 1, 1, 1, 0], [1, 0, 1, 1, 1], [1, 1, 0, 1, 0], [1, 1, 1, 0, 1], [0, 1, 0, 1, 0]])
# 颜色矩阵
C = np.zeros([1, 5])
k = 0
sum = 0#解决方案个数，置为全局变量，画图用
flag = 0#迭代次数，置为全局变量，画图用
listtimes = []#迭代次数列表，置为全局变量，画图用
listsum = []#解决方案个数列表，置为全局变量，画图用
# 判断颜色是否有效
def judge_color(Graph, k, C):
    for i in range(len(Graph[k])