基于Matlab的电磁场与波“镜像电荷法”仿真——平面导体劈的点电荷镜像

已于 2022-04-05 18:57:33 修改
阅读量3.2k 收藏 43
点赞数 13
分类专栏： 仿真 文章标签： matlab 电磁学
于 2022-04-04 14:26:45 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.csdn.net/qq_55710894/article/details/123953071
版权

0、代码中用到的drawEline函数

在使用代码前记得把这个函数和仿真文件放到一个文件夹下哦

function pipi=drawEline(h1,d1,d2)
 
posAxes = get(gca, 'Position');  %获取当前坐标区位置信息
posX = posAxes(1);
posY = posAxes(2);
width = posAxes(3);
height = posAxes(4);%分解位置信息
hold on;
limX = get(gca, 'Xlim');%获取x轴范围
limY = get(gca, 'Ylim');%获取y轴范围
minX = limX(1);
maxX = limX(2);
minY = limY(1);
maxY = limY(2);
x=[h1(1).XData(d1) h1(1).XData(d2)];
y=[h1(1).YData(d1) h1(1).YData(d2)];
xNew = posX + (x - minX) / (maxX - minX) * width;
yNew = posY + (y - minY) / (maxY - minY) * height;%通过坐标变换得到箭头的绝对坐标
pipi=annotation('arrow', xNew, yNew);

1.目的：

运用镜像电荷计算方法和模拟几种典型情况的电荷电位，并用MATLAB进行仿真。

2.理论分析：

由镜像法可知，对于夹角为θ=2Π/n的导体劈，则其对应的镜像电荷数为2n-1个，分别位于每一个镜像区域中，正负号交替出现。

其中电荷量：q=1e-6

常系数：k= 8.9875e9

3.源代码与结果：

3.1点电荷位于无限大导体平面上方：

3.1.1原理：

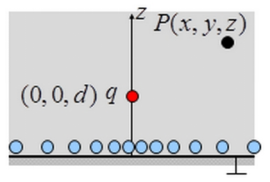
 3.1.2二维图源代码：

[x,y]=meshgrid(-20:1:20,-20:1:20); 
Xi=1;
h=7.2;
q1=4*pi*Xi;
q2=-q1; 
U=(q1./sqrt(x.^2+(y-h).^2) + q2./sqrt(x.^2+(y+h).^2))./4*pi*Xi;
S=-10:0.8:10; 
contour(x,y,U,S,'--');
[Ex,Ey]=gradient(-U);
hold on
plot(0,h,'o','MarkerSize',5);
plot(0,-h,'o','MarkerSize',5);
plot([-20,20],[0,0],'k','linewidth',2);

th1=0:2*pi/20:2*pi;
 
r0=0.65;
x1=r0*cos(th1);
y1=h+r0*sin(th1);
for i=1:20
    line1=streamline(x,y,Ex,Ey,x1(i),y1(i));
    set(line1,'LineWidth',1);
    if i>2 && i <10
        pipi=drawEline(line1,100,101);
    elseif i >=14  && i<=18
        pipi=drawEline(line1,70,71);
    else
        pipi=drawEline(line1,150,151);
    end
    set(pipi,'HeadWidth',7,'HeadLength',7,'Color','b')
end
    
x2=r0*cos(th1);
y2=-h+r0*sin(th1);
for i=13:19
    line2=streamline(x,y,-Ex,-Ey,x2(i),y2(i));
    set(line2,'LineWidth',1);
    pipi=drawEline(line2,100,101);
    set(pipi,'HeadWidth',7,'HeadLength',7,'Color','b')
end

fill([-20,20,20,-20],[0,0,-20,-20],'w');

contour(x,y,U,S,'--');
r0=0.65;
x1=r0*cos(th1);
y1=h+r0*sin(th1);
for i=1:20
    line1=streamline(x,y,Ex,Ey,x1(i),y1(i));
    set(line1,'LineWidth',1,'linestyle','--');
    if i>2 && i <10
        pipi=drawEline(line1,100,101);
    elseif i >=14  && i<=18
        pipi=drawEline(line1,70,71);
    else
        pipi=drawEline(line1,150,151);
    end
    set(pipi,'HeadWidth',7,'HeadLength',7,'Color','b')
end
    
x2=r0*cos(th1);
y2=-h+r0*sin(th1);
for i=13:19
    line2=streamline(x,y,-Ex,-Ey,x2(i),y2(i));
    set(line2,'LineWidth',1,'linestyle','--');
    pipi=drawEline(line2,100,101);
    set(pipi,'HeadWidth',7,'HeadLength',7,'Color','b')
end

title('点电荷对无限大接地导体平面的镜像')  ;
xlabel('x') ;
ylabel('y');

3.1.3二维图截图：

完善前

完善后

 3.1.4三维图代码：

[x,y]=meshgrid(-25:1:25,-25:1:25); 
Xi=1;
h=7.2;
q1=4*pi*Xi;
q2=-q1; 
U=(q1./sqrt(x.^2+(y-h).^2) + q2./sqrt(x.^2+(y+h).^2))./4*pi*Xi;
u0=(q1./1.5 + q2./12.9)./4*pi*Xi;
u = linspace(-8*u0,8*u0,501);
x = linspace(-0.3,0.3,60);
y = linspace(-0.16,0.16,60);
[X,Y] = meshgrid(x);
[Ex,Ey] = gradient(-U);
E = sqrt(Ex.^2 + Ey.^2);
Ex = Ex./E;
Ey = Ey./E;
surf(U);
hold on
shading interp;

subplot(2,1,1);
[c,h]=contour3(U,u);
colormap(jet);
h.EdgeColor='c';

subplot(2,1,2);
[c,h]=contour3(U,u);
colormap(white);
h.EdgeColor='w';
% % h.LineStyle='--';
h1=streamslice(Ex,Ey);
set(h1,'Color',[0.1 0.9 0.8]);
for j=1:length(h1)
    ui = interp2(U,h1(j).XData,h1(j).YData);
    h1(j).ZData = ui;
end

3.1.5三维图截图：

完善前

完善后

3.2点电荷位于60度导体劈：

3.2.1原理：

在夹角为六十度的导体劈中放置一个点电荷（为简化模型，不妨将电荷放置于导体劈的60度角平分线上），则

 3.2.2二维图源代码：( 这个做起来最难受了，叠了好几层，想了好久)

k = 8.9875e9;
d = 0.05;
b = d/sqrt(3);
q0 = 1e-6;
q1 = -q0;
q2 = q0;
q3 = -q0;
q4 = q0;
q5 = -q0;
 
axis([-0.1 0.1 -0.1 0.1])

x = linspace(-0.1,0.1,100);
y = linspace(-0.1,0.1,100);
[X,Y] = meshgrid(x,y);
 
r0 = sqrt((X - d).^2 + (Y - b).^2);
r1 = sqrt(X.^2 + (Y - 2*b).^2);
r2 = sqrt((X + d).^2 + (Y - b).^2);
r3 = sqrt((X + d).^2 + (Y + b).^2);
r4 = sqrt(X.^2 + (Y + 2*b).^2);
r5 = sqrt((X - d).^2 + (Y + b).^2);
U = k * q0./r0 + k * q1./r1 + k * q2./r2 + k * q3./r3 + k * q4./r4 + k * q5./r5;
u = linspace(-5000000,5000000,101);
[C,H] = contour(X,Y,U,u,'k-');
contour(X,Y,U,u,'c-');
% plot( d,b,'r.','MarkerSize',20);
hold on;

x = linspace(0,0.1,100);
y = linspace(0,0.1,100);
[X,Y] = meshgrid(x,y);
r0 = sqrt((X - d).^2 + (Y - b).^2);
r1 = sqrt(X.^2 + (Y - 2*b).^2);
r2 = sqrt((X + d).^2 + (Y - b).^2);
r3 = sqrt((X + d).^2 + (Y + b).^2);
r4 = sqrt(X.^2 + (Y + 2*b).^2);
r5 = sqrt((X - d).^2 + (Y + b).^2);
U = k * q0./r0 + k * q1./r1 + k * q2./r2 + k * q3./r3 + k * q4./r4 + k * q5./r5;
u = linspace(-500000,5000000,1001);
[Ex,Ey] = gradient(-U);
E = sqrt(Ex.^2 + Ey.^2);
Ex = Ex./E;
Ey = Ey./E;
th=linspace(0,2*pi,30);
x1=d+0.0001*cos(th);
y1=b+0.0001*sin(th);
for i=1:30
    h1 = streamline(X,Y,Ex,Ey,x1(i),y1(i));
    set(h1,'LineWidth',1);
    pipi=drawEline(h1,280,281);
    set(pipi,'HeadWidth',4,'HeadLength',4,'Color','k')
end
 

x = linspace(-0.1,0,100);
y = linspace(0,0.1,100);
[X,Y] = meshgrid(x,y);
r0 = sqrt((X - d).^2 + (Y - b).^2);
r1 = sqrt(X.^2 + (Y - 2*b).^2);
r2 = sqrt((X + d).^2 + (Y - b).^2);
r3 = sqrt((X + d).^2 + (Y + b).^2);
r4 = sqrt(X.^2 + (Y + 2*b).^2);
r5 = sqrt((X - d).^2 + (Y + b).^2);
U = k * q0./r0 + k * q1./r1 + k * q2./r2 + k * q3./r3 + k * q4./r4 + k * q5./r5;
u = linspace(-500000,5000000,1001);
[Ex,Ey] = gradient(-U);
E = sqrt(Ex.^2 + Ey.^2);
Ex = Ex./E;
Ey = Ey./E;
th=linspace(0,2*pi,30);
x1=-d+0.0001*cos(th);
y1=b+0.0001*sin(th);
for i=1:30
    h1 = streamline(X,Y,Ex,Ey,x1(i),y1(i));
    set(h1,'LineWidth',1,'linestyle','--');
    pipi=drawEline(h1,280,281);
    set(pipi,'HeadWidth',4,'HeadLength',4,'Color','b')
end

x = linspace(0,-0.1,100);
y = linspace(0,-0.1,100);
[X,Y] = meshgrid(x,y);
r0 = sqrt((X - d).^2 + (Y - b).^2);
r1 = sqrt(X.^2 + (Y - 2*b).^2);
r2 = sqrt((X + d).^2 + (Y - b).^2);
r3 = sqrt((X + d).^2 + (Y + b).^2);
r4 = sqrt(X.^2 + (Y + 2*b).^2);
r5 = sqrt((X - d).^2 + (Y + b).^2);
U = k * q0./r0 + k * q1./r1 + k * q2./r2 + k * q3./r3 + k * q4./r4 + k * q5./r5;
u = linspace(-500000,5000000,1001);
[Ex,Ey] = gradient(-U);
E = sqrt(Ex.^2 + Ey.^2);
Ex = Ex./E;
Ey = Ey./E;
th=linspace(0,2*pi,30);
x1=-d+0.0001*cos(th);
y1=-b+0.0001*sin(th);
for i=1:30
    h1 = streamline(X,Y,Ex,Ey,x1(i),y1(i));
    set(h1,'LineWidth',1,'linestyle','--');
    pipi=drawEline(h1,285,284);
    set(pipi,'HeadWidth',4,'HeadLength',4,'Color','b')
end

x = linspace(0.1,0,100);
y = linspace(0,-0.1,100);
[X,Y] = meshgrid(x,y);
r0 = sqrt((X - d).^2 + (Y - b).^2);
r1 = sqrt(X.^2 + (Y - 2*b).^2);
r2 = sqrt((X + d).^2 + (Y - b).^2);
r3 = sqrt((X + d).^2 + (Y + b).^2);
r4 = sqrt(X.^2 + (Y + 2*b).^2);
r5 = sqrt((X - d).^2 + (Y + b).^2);
U = k * q0./r0 + k * q1./r1 + k * q2./r2 + k * q3./r3 + k * q4./r4 + k * q5./r5;
u = linspace(-500000,5000000,1001);
[Ex,Ey] = gradient(-U);
E = sqrt(Ex.^2 + Ey.^2);
Ex = Ex./E;
Ey = Ey./E;
th=linspace(0,2*pi,30);
x1=d+0.0001*cos(th);
y1=-b+0.0001*sin(th);
for i=1:30
    h1 = streamline(X,Y,Ex,Ey,x1(i),y1(i));
    set(h1,'LineWidth',1,'linestyle','--');
    pipi=drawEline(h1,285,284);
    set(pipi,'HeadWidth',4,'HeadLength',4,'Color','b')
end


fill([0,0,0.1/sqrt(3)],[0,0.1,0.1],'w','edgecolor','w');

x = linspace(0,0.1,100);
y = linspace(0,0.1,100);
[X,Y] = meshgrid(x,y);
r0 = sqrt((X - d).^2 + (Y - b).^2);
r1 = sqrt(X.^2 + (Y - 2*b).^2);
r2 = sqrt((X + d).^2 + (Y - b).^2);
r3 = sqrt((X + d).^2 + (Y + b).^2);
r4 = sqrt(X.^2 + (Y + 2*b).^2);
r5 = sqrt((X - d).^2 + (Y + b).^2);
U = k * q0./r0 + k * q1./r1 + k * q2./r2 + k * q3./r3 + k * q4./r4 + k * q5./r5;
u = linspace(-500000,5000000,1001);
[Ex,Ey] = gradient(-U);
E = sqrt(Ex.^2 + Ey.^2);
Ex = Ex./E;
Ey = Ey./E;
th=linspace(0,2*pi,30);
x1=d+0.0001*cos(th);
y1=b+0.0001*sin(th);
for i=1:30
    h1 = streamline(X,Y,Ex,Ey,x1(i),y1(i));
    set(h1,'LineWidth',1,'linestyle','--');
%     pipi=drawEline(h1,170,171);
%     set(pipi,'HeadWidth',7,'HeadLength',7,'Color','b')
end

x = linspace(-0.1,0.1,100);
y = linspace(-0.1,0.1,100);
[X,Y] = meshgrid(x,y);
r0 = sqrt((X - d).^2 + (Y - b).^2);
r1 = sqrt(X.^2 + (Y - 2*b).^2);
r2 = sqrt((X + d).^2 + (Y - b).^2);
r3 = sqrt((X + d).^2 + (Y + b).^2);
r4 = sqrt(X.^2 + (Y + 2*b).^2);
r5 = sqrt((X - d).^2 + (Y + b).^2);
U = k * q0./r0 + k * q1./r1 + k * q2./r2 + k * q3./r3 + k * q4./r4 + k * q5./r5;
u = linspace(-5000000,5000000,101);
[C,H] = contour(X,Y,U,u,'k-');
contour(X,Y,U,u,'c-');

plot([0,0.1/sqrt(3)],[0,0.1],'k-','LineWidth',3);
plot([0,0.1],[0,0],'k-','LineWidth',3);%画出导体劈
plot( d,b,'r.','MarkerSize',20);
plot( -d,b,'r.','MarkerSize',20);
plot( 0,sqrt(b^2+d^2),'y.','MarkerSize',20);
plot( 0,-sqrt(b^2+d^2),'r.','MarkerSize',20);
plot( -d,-b,'y.','MarkerSize',20);
plot( d,-b,'y.','MarkerSize',20);
title('镜像法——60度导体劈 ','fontsize',15);

3.2.3二维图结果：

完善前

 

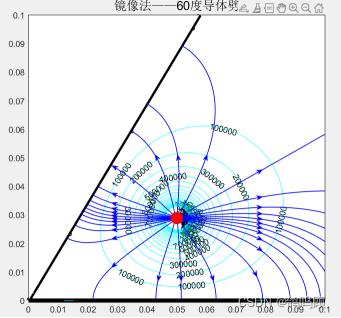
完善后

 

 3.2.4三维图源代码：

k = 8.9875e9;
d = 0.05;
b = d/sqrt(3);
q0 = 1e-6;
q1 = -q0;
q2 = q0;
q3 = -q0;
q4 = q0;
q5 = -q0;
%题目中的电荷，半径等参数

x = linspace(-0.1,0.1,118);
y = linspace(-0.1,0.1,118);
[X,Y] = meshgrid(x,y);
%生成网格

r0 = sqrt((X - d).^2 + (Y - b).^2);
r1 = sqrt(X.^2 + (Y - 2*b).^2);
r2 = sqrt((X + d).^2 + (Y - b).^2);
r3 = sqrt((X + d).^2 + (Y + b).^2);
r4 = sqrt(X.^2 + (Y + 2*b).^2);
r5 = sqrt((X - d).^2 + (Y + b).^2);
U = k * q0./r0 + k * q1./r1 + k * q2./r2 + k * q3./r3 + k * q4./r4 + k * q5./r5;
%由已知值计算出电势表达式

u = linspace(-40000000,40000000,2001);
[Ex,Ey] = gradient(-U);
E = sqrt(Ex.^2 + Ey.^2);
Ex = Ex./E;
Ey = Ey./E;
%求出电场的值

surf(U);
hold on
shading interp;

subplot(2,1,1);
[c,h]=contour3(U,u);
colormap(jet);
h.EdgeColor='c';

subplot(2,1,2);
[c,h]=contour3(U,u);
colormap(white);
h.EdgeColor='w';
% % h.LineStyle='--';
h1=streamslice(Ex,Ey);
set(h1,'Color',[0.1 0.9 0.8]);
for j=1:length(h1)
    ui = interp2(U,h1(j).XData,h1(j).YData);
    h1(j).ZData = ui;
end

3.2.5三维图结果：

完善前

 完善后

 

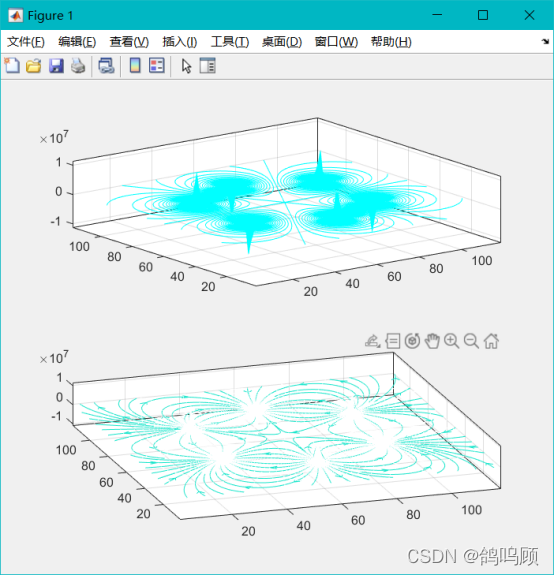
（三维图的部分完善了个寂寞，感觉还不如一开始的样子）

电磁场与电磁波（7）——唯一性定理的应用：镜像法
Lmhark的博客
11-05 1万+
镜像法是用一组适当配置的电荷系统来替代要求解的给定系统。根据唯一性定理，只要新添加的电荷（镜像电荷）不进入原求解区域，以保证不改变原求解区域内的电荷分布，就能保证不改变原求解区域内的电位方程，并且原区域边界处的条件保持不变就可满足要求。镜像法实际上是用在求解区域外添加的电荷来替代原有边界对系统的影响，因此，在使用镜像法时，首先把原有的边界去掉，再在求解区域外适当添加若干电荷，调整电荷数量、电荷量和位置，使得在原有边界处的条件不变。这样根据唯一性定理，新系统的解在原求解区域中就是原系统的解。
MATLAB仿真镜像法.pdf
10-07
MATLAB仿真镜像法.pdf
基于Matlab的电磁场与波“镜像电荷法”仿真——点电荷位于半球形凸起导体附近
qq_55710894的博客
04-04 3080
点电荷位于半球形凸起导体附近，下半球实现了虚线绘制
基于Matlab的电磁场与波“镜像电荷法”仿真——导体球外点电荷的几种情况
qq_55710894的博客
01-29 8799
一、绘制箭头的函数 drawEline函数 作者：顾世杰，戴桢琦 1、目的 本次MATLAB仿真几乎每一个项目的二维图都需要画电场线，按照老师的要求，电场线头尾必须与电荷连接，因此我们选择使用streamline函数画电场线，由于streamline函数本身画出的线不带箭头，我们通过研究上一届学长学姐们的资料，研究并改良了其中画箭头的代码语句，将其做了必要的扩充，并封装成一个函数M文件。 2、源代码 functiondrawEline(h1,d1,d2)...
基于Matlab的点电荷镜像法电场的可视化.pdf
06-23
点电荷的镜像法是“电磁场与电磁波”课程的重要内容。这部分的教学重点通常在于分析镜像法原理和寻找镜像电荷,但是缺乏对镜像电场空间分布的图形描绘。本文用Matlab软件对镜像电场进行仿真,绘制了点电荷镜像法中多种镜像电场的等位面和电力线细节图,对镜像电场进行了可视化。可视化有利于加深学生对镜像法原理、镜像电荷和镜像电场分布的理解。
镜像法解决电磁场问题
11-23
镜像法解决电磁场问题，mathematics工具解决镜像法，原理介绍
MATLAB仿真镜像法.docx
07-05
MATLAB仿真镜像法是一种利用先进的计算软件MATLAB进行电磁场计算的技术，尤其适合处理与镜像电荷相关的问题。镜像法在解决静电边值问题中扮演着重要角色，特别是在分析电荷靠近导体平面时的电场分布情况。本文档以线...
电动力学中导体球镜像电荷分布及其电容特性研究（可复现，有问题请联系博主）
最新发布
03-19
内容概要：本文详细阐述了利用镜像法分析导体球周围镜像电荷的分布规律及导体球的电势、电容变化情况，涵盖了从一般情况推导通项公式到针对特定条件下的特殊情况讨论，并结合Matlab软件绘制相关图像，直观展示各参数...
镜像电荷法无限长直导线仿真
01-05
### 使用镜像电荷法对无限长直导线进行电磁场仿真 对于无限长直导线周围的电场计算，可以通过引入镜像电荷简化问题求解过程。当考虑一根位于 \(z\) 轴上的无限长带电线，在其附近存在一块接地的理想导体平面时，...
【高频电磁波理论基础】电磁波的反射、折射与衍射现象
![【高频电磁波理论基础】电磁波的反射、折射与衍射现象]...## 1.1 电磁波的定义与历史 电磁波是一种能在空间中传播的波动现象，由相互垂直的电场和磁场组成。它以波动形式传递能量和
深度解析COMSOL中的瞬变电磁法模拟：掌握物理场设置的秘诀
首先概述了COMSOL软件的基本功能以及瞬变电磁法的基本概念，随后详细阐述了在COMSOL中设置物理场、定义材料属性、网格划分、边界条件设置、后处理分析等关键步骤。文章通过实际案例演练，展示了模拟过程中的实战技巧...
电磁场matlab仿真代码-moveCharge:电荷在静态电磁场中的运动
05-24
电磁场matlab仿真代码电荷在静态电磁场中的运动 编程语言：MATLAB 计划目标 电荷在静态电磁场中的运动是基于诸如库仑定律或比奥-萨瓦特定律等基本定律的各种微观现象的完美示例。 以下论文中提出的物理现象与电动力学的经典定义相对应，归结为对带有定义电荷的物理体行为的分析。 不幸的是，通常不可能对这种类型的关系进行分析。 因此，该项目使用有限差分法。 解决方法 问题涉及电荷在其他电荷和导体随电流产生的静电场中移动。 问题减少到二维空间。 此模拟的主要部分基于中央有限差分技术（或也实现了Euler方法）。 从洛伦兹力和第二牛顿定律（对于二维情况）开始，电荷位置由一组微分方程确定。 作为游戏应用 当具有必要的计算工具时，将创建一个图形界面，在该界面中，用户在了解物理定律的情况下，试图根据电流将其他电荷和导体确定出电场中移动电荷的路径。 为此，他要经历各种难度级别（通常是反复试验），其中包括电荷和导体的更复杂配置。 可以通过以下操作序列来简要描述此想法： 用户选择难度级别（电荷和导体的数量）。 产生电荷和/或导体的随机配置，并确定所考虑的电荷的轨迹（该配置和轨迹对用户不可见）。 根据计算出
csm_csm_模拟电荷法_电场计算_
10-03
基于模拟电荷法的计算高压架空输电线下二维电场的数值计算
通信与网络中的基于Matlab的均匀平面电磁波的仿真
10-20
摘要：在电磁场与电磁波的教学中，应用Matlab编程对电磁场的分布和电磁波的传输进行仿真，使得抽象的概念直观化，有助于学生对于电磁场和电磁波教学内容的学习。着重仿真了均匀平面电磁波的传播、极化、反射和折射的动态过程。 　　0 引言 　　“电磁场与电磁波”是电子与通信类专业本科生必修的一门专业基础课，课程涵盖的内容是电子与通信类专业本科阶段所应具备的知识结构的重要组成部分。 　　在教学过程中，学生普遍反映该门课程比较抽象，包含了大量的数学公式推导，很多概念难以理解。无论是电磁场还是电磁波，都是看不到、摸不着的，教师难讲、学生难懂是当前该门课程教学中普遍存在的现象。 　　Matlab由于其
导体接地matlab,电磁场与电磁波课程的Matlab辅助学习.docx
weixin_29661213的博客
03-18 387
电磁场与电磁波课程的Matlab辅助学习电磁场与电磁波课程的Matlab辅助学习姓名: 学号: 090260318专业: 电子科学与技术指导老师: 电磁场与电磁波课程的Matlab辅助学习 摘要: 为了学习电磁学的可视化，我们在电磁场与电磁波的课程学习中引入 Matlab 软件工具。本文针对课程中的难点和重点,利用 Matlab 工具箱及各类函数, 对于具体的实例给出了仿真结果。Matlab软...
【电场】基于模拟电荷法计算输电线路铁塔周围电场分布附matlab代码
qq_59747472的博客
08-14 1008
为了提高模拟电荷法计算电场的精度并降低其计算复杂度,采用黄金分割法对模拟电荷法进行优化,提出了一种精度高且易实现的模拟电荷设置方法.应用该模拟电荷法计算了直流输电线路导线表面电场,采用"化曲为直"法绘制了电场线轨迹.在此基础上,基于通量线法对比分析了分裂导线表面最大场强在不同取值方法下求解合成电场和离子流密度时带来的计算结果差异.结果表明:此优化模拟电荷法计算电场精度高,并能随导线参数的变化灵活调整模拟电荷的设置;"化曲为直"法绘制电场线轨迹,可避免地面电场水平分量为0时微分方程结果不收敛的问题;.....
带电缺陷计算中镜像电荷相互作用修正
PWmat的博客
05-05 805
近日，来自中科院半导体所超晶格实验室的索曌君等人，在Physical Review B上发表了标题为“Image charge interaction correction in charged-defect calculations”的研究工作。骆军委研究员参与了论文的指导工作。论文对镜像电荷作用进行了严格的推导，并提出了C-AP和C-SC两种方法，来修正镜像电荷作用。
镜像法的理解——工程电磁场 P9
m0_52555753的博客
12-15 3081
电磁场
采用镜像电荷法画出接地导体球（半径=a）和距离球心d1（d>a）的点电荷q所构成的静电场的电场和电位立体分布,并分析其特点。（可采用MATLAB绘图采用球坐标实现）
12-26
### 使用MATLAB绘制接地导体球与外部点电荷的静电场 为了实现这一目标，可以采用镜像电荷法来求解该问题。具体来说，在距离球心 \( d_1 \) 处放置一个实际点电荷 \( q \)，则可以在球内找到一个位置使得引入的虚设电荷能够满足边界条件——即球表面保持零电势。 #### 镜像电荷的位置和大小 对于位于 \( (0, 0, d_1) \) 的正电荷 \( q \)，其对应的负镜像电荷 \( -\frac{a^2}{d_1} \)[^1]。这里 \( a \) 是导体球的半径，而 \( d_1 \) 表示外置点电荷到球中心的距离。因此，\( q'=\left(\frac{a}{d_1}\right)^3q \)。 #### 计算总电位 整个空间内的任意一点 P(x,y,z) 上总的电位 V 可由这两个电荷共同贡献得出： \[V(P)=k_e\left[\frac{q}{r_{PQ}}-\frac{\left(a/d_1\right)^3q}{r_{PR'}}\right]\] 其中 \( k_e=8.99\times10^{9}Nm^2/C^2 \) 是库仑常数；\( r_{PQ}=|QP| \), \( r_{PR'}=|QR'| \) 分别代表从 Q 和 R’ 到 P 点的距离向量长度。 #### 绘制等位面图 利用上述公式编写 MATLAB 脚本以生成三维网格数据，并调用 `surf` 函数展示不同高度上的等位线图形。下面是一个简单的例子: ```matlab % 参数设定 ke = 8.99e9; % Coulomb's constant a = 1; % Sphere radius d1 = 2*a; % Distance of point charge from sphere center q = 1; % Charge value [X,Y,Z]=meshgrid(linspace(-3*a,3*a,50)); R=sqrt(X.^2+Y.^2+(Z-d1).^2); Rp=sqrt(X.^2+Y.^2+(Z+a^2./d1).^2); V=(ke*q*(1./R-(a/d1)^3./(Rp))); figure; isosurface(X,Y,Z,V,-Inf,'FaceColor','red','EdgeColor','none'); hold on; contourslice(X,Y,Z,V,X(1,:),[],[]); colorbar; xlabel('X axis'); ylabel('Y axis'); zlabel('Z axis'); title(['Potential Distribution around Grounded Conducting Sphere and Point Charge']); axis equal tight vis3d; view([30 30]); shading interp; lightangle(45,30); camlight headlight; material shiny; ``` 此脚本创建了一个包含多个切片视图的图像窗口，用于表示围绕着带有点电荷的接地金属球周围的电位分布情况。 #### 特性分析 当存在这样的配置时，由于导体内部不存在净自由电荷，所以所有的感应电荷都集中在表面上形成均匀分布的状态。这导致了在靠近导体的地方出现了强烈的局部畸变效应，而在远离区域逐渐趋于正常的空间衰减趋势。此外，因为采用了镜像方法处理边界条件，故而保证了导体表层始终维持在一个固定的零伏特水平上。
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

鸽呜顾

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值