质点振动学
1-1质点振动系统的概念
集中参数系统:构成整个振动系统的质量块与弹簧,他们的运动状态都是均匀的。
1-2质点的自由振动

这个地方的胡克定律都是之前学的但是这本书用的字母会不太一样
Km是弹性系数
Cm=1/Km是顺性系数
在分析问题的时候最重要的就是利用牛顿第二定律将问题的平衡条件方程化成
这种形式,名为质点的自由振动方程。其中
角频率。
解自由振动方程的时候,认为其次二阶常微分方程的一般解为
A和B两个常数由初始条件来决定,其中里面的参数就不做多解释了,在大学物理中都有解释。
重点是系统的固有频率。由此可看出这是一个常数与系统自己本身的性质有关,降低固有频率:
(1)增加系统质量(2)减小弹性系数
系统总能量为一个常数
双弹簧连接情况:这里可以借鉴电路中电阻的串并联情况,与电阻的情况相反,与电导的情况相同。这里再推理的时候用到一个物理量叫静位移,就是在只有重力的条件下弹簧的伸长量。


串联等效弹性系数
并联
在现实情况中一般弹簧不是理想情况,是具有质量的。
这里运用微分思想将弹簧分成无数小段,所以每一小段弹簧产生的位移再利用动能定理算出每份小弹簧的动能,再以长度为自变量进行积分,积分长度为l,加上之前的物块总能量为
其中把速度v用牛顿第二定律表示出来再代入式子中可以得到
显然在考虑了弹簧的质量之后,系统的固有频率降低。
因为振动问题是数学物理方程这门学科中被认为偏微分方程的,它也可以用欧拉公式换成复数来解,类似于电路。
1-3质点的衰减运动
考虑到阻力,小振动运动的阻力可以认为Rm称为阻尼系数,之前的自由振动方程改写为
,在为了解决方程引入一个新变量
叫他衰减系数于是方程变为
这个称为质点的衰减运动方程。设解为复数解,
,将其代入方程后得出
及
这个地方为了适应所用的情况以及后面求系统的能量的时候会用到把A和B这两个常数也设成了复数
最后得到
其中
具体过程如下


把衰减到振幅的1/e倍的时间称为衰减模量
得到了一个推论:第一次与第i次的振幅比为
衰减振动的能量用通式然后往里带
反正这个我也不想知道怎么算出来的。。。。。。

1-4质点的强迫运动

跟之前的每一节一样都会加一个新的力,这节加的是强迫力,也就是一种能用数学式子表示出来的外力之一,
再按照之前的套路把方程改一下就变成了
我们再化成通用的复数形式变成质点强迫振动方程
解方程时设代入方程得到解为
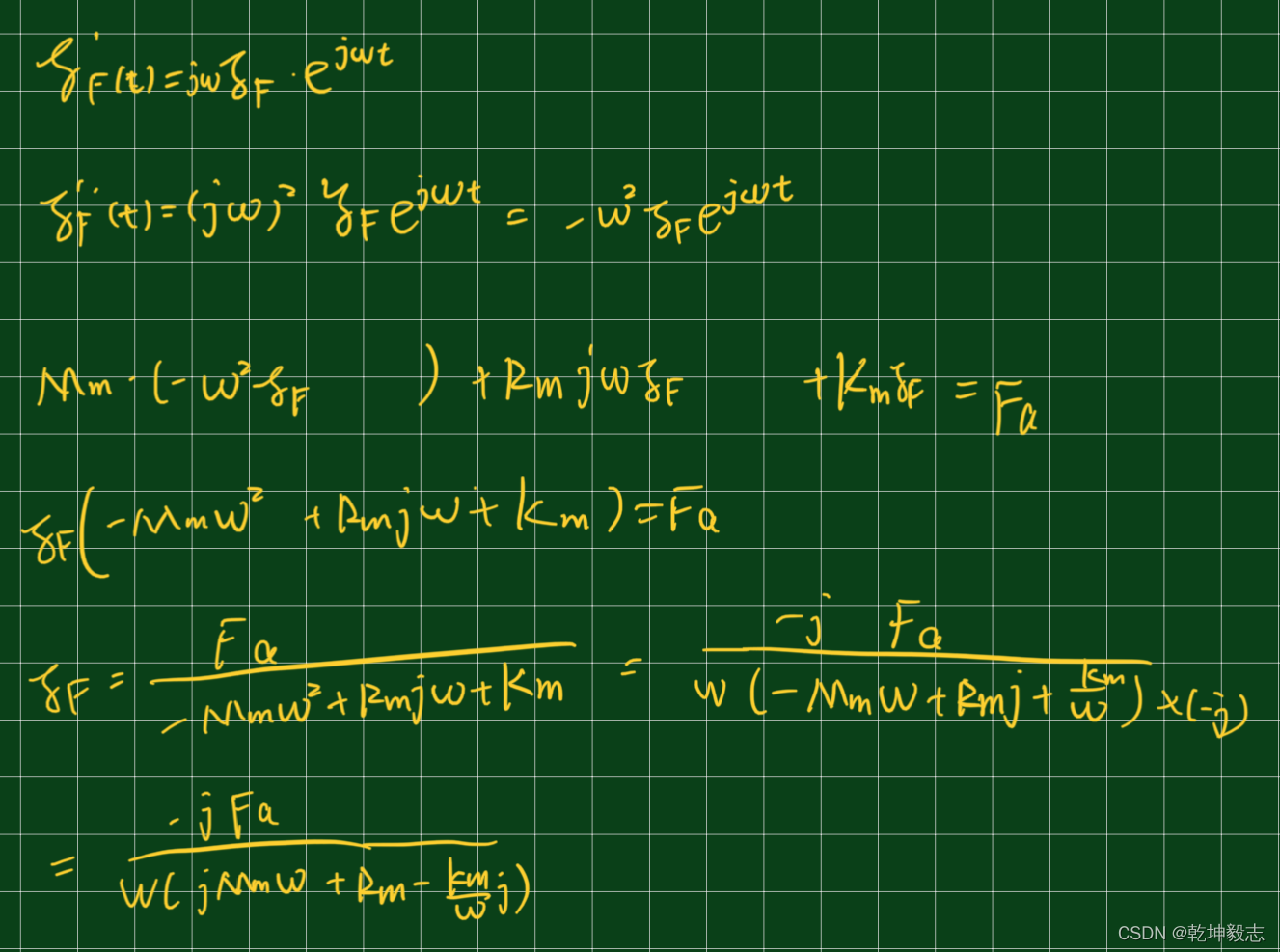 式子中
式子中称为系统的力阻抗,Rm叫力阻。
为力抗,这里可以类比电路里的电阻和电抗。
由(1-4-7)得到(1-4-8)过程:

这个方程就是在之前衰减振动的方程上加了一个强迫项,如此根据之前的解再加上一个强迫项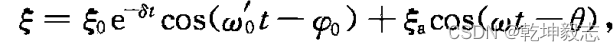
第一项为瞬态解,第二项为稳态解,可直接根据字面意思理解。
书上引入了一个新的物理量力学品质因数


A: Qm> 时曲线在z=zr处有峰值系统才会共振,
书上对于A,B,C三个方向进行了分析都是为了得到三个结论
B:如果用来表示系统共振频带的宽度,那么其带宽正好等于品质因素Qm的倒数。
C:Qm越大加速度共振峰越高。
三个曲线都是Qm越大,共振峰越高且尖。
一个周期的平均损耗功率为
电声器件的工作有三个控制区:质量,弹性,力阻书上概念直接看就行。
1-5周期里的强迫振动
本节里加入了周期力,需要用到傅里叶级数。这个位置可以去看一下数学物理方程这门学科或高等数学再复习一下。同样是写出振动方程
其中

解法跟前面一样先是把
换成复数形式带入其中

即可得到与之前相类似的力的阻抗形式

























 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








