目录
回顾一下协同过滤
矩阵分解可以被视为一种 改进版的协同过滤。也可以说是协同过滤的一种 优化方法。
如果你想学习矩阵分解但还没学习过协同过滤,建议可以先了解一下协同过滤算法哦😊:
协同过滤存在问题:数据稀疏性
- 在大规模系统中,用户与物品之间的共现矩阵通常是稀疏的,许多评分或交互记录是缺失的,因为用户通常只会对少数物品进行交互反馈。
- 传统的基于相似度的方法依赖于计算所有用户之间或物品之间的相似度,这个方法无法将两个物品相似的信息推广到其他物品相似度的计算上。(泛化性弱)
- (理解一下:用户A对物品a和b评价,用户B对物品b和c评价,用户C对物品c和物品d评价,则协同过滤无法计算到物品a和d的相似度)
- 导致问题:热门物品具有很强的头部效应,容易与大量物品产生相似性。冷门物品则很难被推荐。
矩阵分解——改进版的协同过滤
矩阵分解含义:将 记录用户和物品交互信息的共现矩阵 分解成 一个用户矩阵 和 一个物品矩阵 ,从而使得数据可以以一种低维的方式表示。( m*n 规模的矩阵分解为 m*k 和 k*n 的两个矩阵,其中k值就是后面我们会提及的隐向量的维度)
(可能你现在会很疑惑为什么要分解矩阵,继续往后看😊)

🌟核心思想:通过将原始矩阵拆分为若干个低秩矩阵来捕捉数据中的潜在关系(即用户和物品之间的潜在特征),并利用这些低维的表示来计算补全缺失值,进而进行个性化推荐。
(💡:所以 矩阵分解的过程 其实可以理解为 对用户和物品的特征进行一个信息浓缩概括的过程)
隐向量:蕴含了用户或物品信息。上图中的用户矩阵的每一行和物品矩阵中的每一列就对应着一个用户或物品的隐向量。
隐向量的维度k:决定了其表达信息能力的大小。k的取值需要经过多次试验找到一个平衡点。(k越大,表达信息能力越强,泛化能力越弱)(上图中用户隐向量维度和物品隐向量维度都为2)
🌟算法流程(前三步与协同过滤无异):
- 构建用户与物品的有向图(有向图的弧表示用户对物品的互动记录)
- 根据有向图构建共现矩阵(横列坐标分别表示用户和物品)
- 问题转变为预测共现矩阵中空缺值的问题
- 填充空缺值,使得共现矩阵变成一个完整的矩阵,为后续的矩阵分解做准备。(最简单可以用用户和物品的平均评分或行为频率进行填充)
- 通过矩阵分解技术将 共现矩阵 矩阵分解为 用户矩阵 和 物品矩阵。矩阵存储了每个用户和物品的隐向量。主要利用梯度下降的方法,目标函数是使得原始共现矩阵与用户向量和物品向量之积的差尽量小。(理解:对用户和物品的特征信息浓缩概括的过程)
- 最后计算用户推荐列表仅需要将由前一步计算得出的用户矩阵与物品矩阵相乘,即可得出与原矩阵规模大小相同的矩阵,其中就预测各个物品的评价。(理解:利用前面浓缩概括的信息(用户矩阵和物品矩阵)进行推导的过程)
🤔那么有童鞋可能会问了:不是在第四步已经把矩阵填充完了吗,而我们的目标不就是预测空缺值吗,是不是任务到第四步已经结束了捏,为什么还要经过这么繁琐的步骤去矩阵分解?(要是能够分清,可以跳过这一部分啦🙂↔️)
💡这里需要说明一下:
- 填充的作用:填充缺失值的目的是为了使得矩阵不再稀疏,可以用来初始化矩阵分解的输入,使得算法有一个“完整”的数据集来进行训练。
- 矩阵分解的作用:矩阵分解在填充的基础上进一步提取出深层次的用户和物品之间的潜在关系,生成潜在因子矩阵,从而提升推荐的准确性。分解后得到的隐向量能够更好地拟合用户的兴趣和物品的特性,而不仅仅是填充值。
矩阵分解的详细求解过程
目前主要有三种方法:
- 特征值分解:只能作用于方阵,不适用。😔
- 奇异值分解:要求共现矩阵是稠密的,与其应用条件相悖,需要补充缺失元素;计算复杂度高,达到了O(mn^2)。😔
- 梯度下降:矩阵分解的主要方法。🤩
因此我们采用梯度下降进行矩阵分解。
目标函数:目的是通过调整 用户向量和物品向量 qi和pu,让原始评分与用户向量和物品向量之积的差尽量小。(差越小代表着对于用户和物品的信息浓缩概括的就越好。)
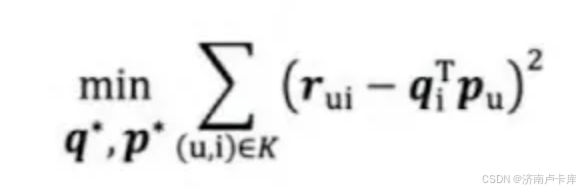
正则化项
为了防止过拟合现象,在上式的基础上加入正则化项:

我们应该怎么理解正则化项呢?
(要是只是想初步了解,那就只需要知道正泽项可以防止过拟合就够啦)



λ为正则化系数:λ越大,则正则化的限制就越强。
可以发现加入正则化后的目标函数所代表的意义:如果用户矩阵或物品矩阵中所代表的隐向量中数值过大的话,会导致正则化项同时增大,这就与目标函数想要优化的方向相悖而行。
因此正则化项的作用:限制用户和物品特征向量的大小,防止特征向量过拟合。特征向量越小,最后拟合的曲线也会更加“平缓”。

回到目标函数的求解过程:
1. 基于上述的目标函数,对qi和pu求偏导

2. 利用求导结果,沿梯度的反方向更新参数

3. 迭代次数到达上限n或者损失值小于阈值时停止更新,得到的最终的用户和物品矩阵
消除用户和物品打分的偏差
存在问题:存在用户给所有交互的物品都给予肯定(或否定)的评价。或者存在物品被用户都给予肯定(或否定)的评价。
解决方案:在目标函数中加入用户和物品的偏差向量。

(详细过程这里就不过多阐述啦,想了解的伙伴可以自行去了解🤓)
矩阵分解的优点以及局限性
🤩优点:
- 泛化能力强:一定程度上解决了数据稀疏的问题
- 空间复杂度低:不用像协同过滤那样存储庞大的用户相似性或物品相似性矩阵,只需要存储隐向量。空间复杂度由O(n^2)下降到O((n+m)*k)
- 更好的扩展性和灵活性:矩阵分解的结果方便与其他特征进行组合和拼接。
🙁局限性:与协同过滤一样,矩阵分解仅仅使用到了用户与物品交互的数据,不方便加入用户、物品和上下文的特征,从而丧失了利用很有有效信息的机会。(后续介绍基于内容的推荐系统就会开始考虑用户、物品和上下文的特征啦,可以期待一手哦😁)
声明:本章内容主要源于王喆老师的《深度学习推荐系统》,是一本很好的推荐系统的书,强力推荐👍。
如果您觉得对您有帮助,请留下宝贵的赞赞吧🥺,我真的很需要。

























 8283
8283

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








