推荐系统2--隐语义模型（LFM）和矩阵分解（MF）

一，背景

协同过滤（userCF，itemCF ）完全没有用到用户或者物品本身的属性，仅仅利用了用户与物品之间的交互信息就可以实现推荐。是一个可解释性很强，非常直观的模型，但是缺点在于：1，处理稀疏矩阵的能力比较弱，泛化能力弱。 为了解决这个问题，从协同过滤中衍生出矩阵分解模型（Matrix Factorization,MF）,并发展出矩阵分解的分支模型,比如隐语义模型和矩阵分解

隐语义模型和矩阵分解可以理解为类似的内容，都是在协同过滤共现矩阵的基础上，使用更稠密的隐形量表示用户和物品，挖掘用户和物品的隐含兴趣和隐含特征，在一定程度上弥补协同过滤模型处理稀疏矩阵能力不足的问题。

二，隐语义模型原理

假设每个用户都有自己的听歌偏好， 比如A喜欢带有小清新的， 吉他伴奏的， 王菲的歌曲，如果一首歌正好是王菲唱的， 并且是吉他伴奏的小清新， 那么就可以将这首歌推荐给这个用户。 也就是说是小清新， 吉他伴奏， 王菲这些元素连接起了用户和歌曲。 当然每个用户对不同的元素偏好不同， 每首歌包含的元素也不一样， 所以我们就希望找到下面的两个矩阵：
1，潜在因子----用户矩阵Q
这个矩阵表示不同用户对于不同元素的偏好程度，1代表很喜欢，0代表不喜欢。如下：

2，潜在因子----音乐矩阵P
表示每种音乐含有各种元素的成分，比如下表中， 音乐A是一个偏小清新的音乐， 含有小清新的Latent Factor的成分是0.9， 重口味的成分是0.1， 优雅成分0.2…

利用上面矩阵，得到张三对音乐A的喜欢程度：
张三对小清新的偏好 * 音乐A含有小清新的成分 + 张三对重口味的偏好 * 音乐A含有重口味的成分 + 张三对优雅的偏好 * 音乐A含有优雅的成分…,

按照这个计算方式，每个用户对每首歌都可以得到相应的评分，最后得到评分矩阵：

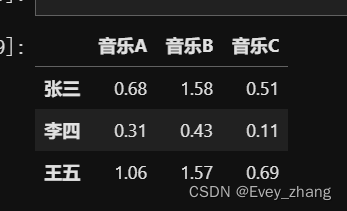
从上面的例子，隐含特征含义如下：
小清新，重口味，优雅，这些可以看做是隐含特征，通过这个隐含特征可以把用户的兴趣和音乐进行分类，其实就是找到了每个用户每个音乐的一个隐向量表达形式，这个隐向量可以反映出用户的兴趣和物品的风格，并能将相似的物品推荐给相似的用户。类似于把协同过滤算法进行了一种延伸，把用户的相似性和物品的相似性通过了一个叫做隐向量的方式进行表达。
但现实中，我们没有上面那两个矩阵，有的只是用户的评分矩阵，并且这个矩阵还非常稀疏（有些用户没有对某些物品进行评价）

针对这个稀疏的矩阵，协同过滤算法想基于用户相似性或者物品相似性去填充这个矩阵不太容易，并且很容易出现长尾问题。所以，协同过滤的延伸：矩阵分解，或者叫隐语义模型渐渐得到了发展

隐语义模型/矩阵分解 的原理：想办法基于最后的评分矩阵，去找到上面例子中的那两个矩阵，也就是用户兴趣和物品的隐向量表达，然后就把这个评分矩阵分解成Q和P两个矩阵乘积的形式，这时就可以基于这两个矩阵去预测某个用户对某个物品的评分了。然后基于这个评分去进行推荐。

三，矩阵分解算法原理

现实中我们得到的是残缺的评分矩阵，通过矩阵分解算法，可以通过分解评分矩阵，得到用户和物品的隐向量，也就是上面的用户矩阵Q和物品矩阵P，下图给出矩阵分解的过程：

矩阵分解算法将MN维的共享矩阵R分解成mk维的用户矩阵U和k*n维的物品矩阵V相乘的形式。其中m是用户数量，n是物品数量，k是隐向量维度，也就是隐含特征个数，只不过这里的隐含特征变得不可解释了，也就是我们不知道具体含义了，要模型自己去学。K的大小决定了隐向量表达能力的强弱，k越大，表达信息就越强，理解起来就是把用户的兴趣和物品的分类划分的越具体了。
有了用户矩阵和物品矩阵，则计算用户u 对物品i 的评分，只需要：

这里的Pu 是用户u 的隐向量，就类似上面的张三向量，并且是一个列向量。qi是物品i的隐向量，就类似上面的音乐A向量，也是一个列向量。所以才用Pu的转置与qi相乘，得到用户的最终评分。pu,k和qk,i 是模型的参数，也是我们需要计算的。pu,k度量的是用户u的兴趣与第k个隐类的关系，qk,i 度量的是第k个隐类与物品i之间的关系。下面来求两个矩阵里面的具体参数。

四，矩阵分解算法的求解

矩阵分解，最常见的方法是特征值分解（EVD）或者奇异值分解（SVD）。但这两种方法不适合直接使用。首先是EVD,它要求分解的矩阵是方阵，显然用户-物品矩阵不满足这个要求，而传统的SVD分解，会要求原始矩阵是稠密的，我们这里得到的用户物品评分矩阵一般情况下是非常稀疏的，如果想用奇异值分解，必须对缺失元素进行填充，而一旦补全，空间复杂度会非常高，而且补的不一定对，并且SVD分解计算复杂度非常高，我们的用户-物品矩阵非常大，所以基本上无法使用。

4.1 Basic SVD

2006年的Netflix Prize之后，Simon Funk 公布了一个矩阵分解算法叫做Funk-SVD，后来被Netflix Prize的冠军Koren称为 Latent Factor Model(LFM)。**Funk-SVD 的思想很简单：把求解上面两个矩阵的参数问题转换成一个最优化问题，可以通过训练集里面的观察值利用最小化来学习用户矩阵和物品矩阵。**具体理解如下：
有了用户矩阵和物品矩阵的话，我们如果想要计算用户u 对物品i的评分，只需要

现在，我们有真实的rui，但是没有pu和qi。那么我们可以初始化一个，随机初始化一个用户矩阵U 和一个物品矩阵V,这样就有pu 和qi了。当然，随机初始化的肯定不准，但是有了pu 和qi之后，就可以计算一个猜测的rui，即：

这时候，猜测和真实值之间会有一个误差：

有了误差，就可以计算出总的误差平方和：

有了误差（也就是损失），我们就可以想办法进行训练，将SSE降到最小，这样我们的两个矩阵参数就计算出来了（这就是训练深度学习模型时候常用的套路），于是就把求解用户矩阵和物品矩阵的问题，转换成了最优化的问题，目标函数是：

这里的K 表示所有用户评分样本的集合。
我们拿到一个用户物品评分矩阵，要去计算两个参数矩阵U和V,可以利用求解神经网络模型参数的思路来计算这两个矩阵：
1.首先先初始化这两个矩阵
2.把用户物品评分矩阵里面那些已经评过分的样本当做训练集的label,把对应的用户和物品的隐向量当做features,这样就会得到（features,label），相当于是训练集
3.通过两个隐向量乘积得到预测值pred
4.根据label 和pred 计算损失
5.反向传播，通过梯度下降的方式，更新两个隐向量的值
6.未评过分的那些样本当做测试集，通过两个隐向量就可以得到测试集的label值
7.这样就填完了矩阵，下一步就可以进行推荐了

得到了目标函数，接下来使用梯度下降算法来降低损失。我们需要对目标函数求偏导，得到梯度。我们的目标函数如果是上面的SSE,下面来推导一下最后的导数：

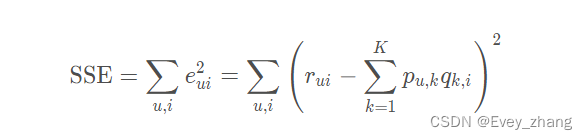
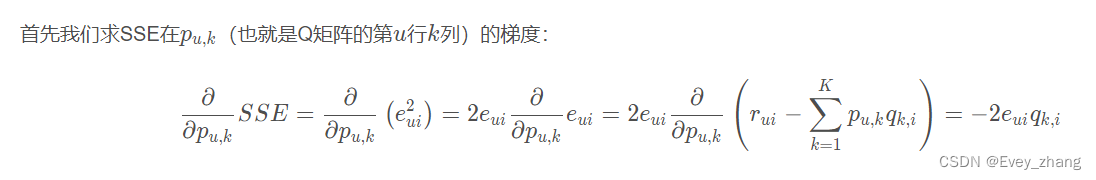
为了让公式更简单，将SSE公式中前面的2约掉，即可以令SSE等于：

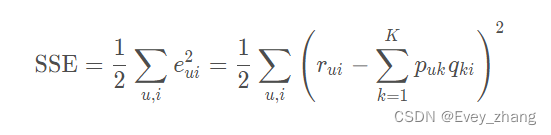
这样，梯度前面就没有系数2了，有了梯度，接下来就可以用梯度下降算法来更新梯度了：

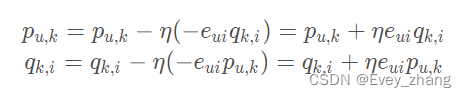
这里的yita 是学习率，用来控制步长。得到了更新的式子，下面讨论更新如何进行。有两种选择：
1，计算完所有已知评分的预测误差（即所有的训练数据）后再对P,Q进行更新。
2，每计算完一个eui后（也就是一个训练数据的预测误差）立即对pu 和 qi 进行更新。
第一种叫做批梯度下降，第二种叫做随机梯度下降。二者的区别在于，批梯度下降在下一轮迭代才能使用本次迭代的更新值，随机梯度下降本次迭代中当前样本使用的值可能就是上一个样本更新的值。由于随机性可以带来很多好处，比如有利于避免局部最优解，所以现在大多倾向于使用随机梯度下降进行更新。这就是运用梯度下降的矩阵分解算法了。称之为Basic SVD.

Basic SVD 算法存在的问题是：当两个矩阵很大的时候，往往容易陷入过拟合的困境，这时，就需要在目标函数SSE 上面加上正则化的损失，就变成了RSVD。

4.2 RSVD

在目标